Отрицательные температуры

Хотя всегда утверждается - и это утверждение правильно,- что абсолютный нуль представляет собой самую низкую из возможных температур, физики часто говорят и об отрицательных температурах.

Пусть атом имеет спин 1/2 и, соответственно, имеет в магнитном поле два состояния с т= ±1/2.

Если магнитный момент атома положителен (g >0), то у большей части атомов спины направлены по полю. Даже при Т= ∞ вероятности обоих направлений, как мы видели, только сравниваются. Это значит, что, сколько бы ни подводить к системе теплоты, нельзя сделать так, чтобы состояние с большей энергией встречалось чаще - было бы больше "населено", чем состояние с меньшей энергией. Тем не менее такой обратной заселенности можно достичь с помощью небольшой хитрости. Для этого надо быстро изменить направление магнитного поля на обратное. Чтобы описать новую ситуацию, надо во всех формулах заменить В на -В. Но это то же самое, что изменить Т на -Т. Распределение спинов после "поворота" поля будет выглядеть так, как будто их температура стала отрицательной. Уровень с большей энергией заселен больше (рис. 29)!

То, что нельзя было сделать, отбирая теплоту, оказалось сравнительно просто сделать, управляя магнитным полем. У системы уровней немного, и переставить их местами оказалось возможным.

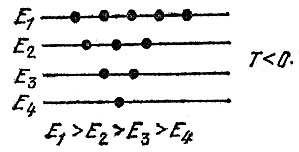
Рис. 29. Распределение при 'отрицательной' температуре

Что будет с такой системой дальше? Ясно, что система спинов будет возвращаться в состояние теплового равновесия. Спины атомов будут переворачиваться благодаря электромагнитному взаимодействию атомов. Избыток энергии будет уходить в другие части системы, и спины атомов распределяются так, как должно быть при температуре Т. Такой процесс очень похож на передачу теплоты - избыток энергии отдается более холодным частям системы. Избыток энергии возник, конечно, когда к системе спинов была добавлена энергия при обращении направления магнитного поля.

Этот результат можно описать и более формально. Для этого запишем отношение "населенностей" двух уровней;

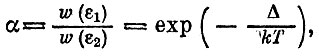
где Δ= ε₁- ε₁ -разность энергий двух уровней. Из формулы видно, что в "нормальной" ситуации, когда Т изменяется от 0 до ∞, а изменяется от 0 до 1; интервалу же изменений а от 1 до когда верхний уровень более заселен, надо сопоставить значения Т от ∞ до 0. Населенность описывается разрывной функцией от Т равной населенности двух уровней отвечают два значения температуры: T= ±∞, так как α (±∞)=1.

Таким образом, относительная населенность верхнего уровня (величина а) описывается температурой несколько парадоксальным образом. Населенность растет, когда температура повышается от нуля до бесконечности. Но T=∞ отвечает не самому большому значению α. Населенность может расти и дальше (от 1 до ∞), если температура будет расти, оставаясь отрицательной, от до 0. В этом смысле можно сказать, что отрицательные температуры лежат "выше" T= ∞, Описание поведения α было бы проще, если бы мы пользовались величиной, Обратной температуре: β=1/T. Нетрудно увидеть, что, когда α изменяется от 0 до ∞, β уменьшается монотонно, без всяких скачков от ∞ до ∞. -"Обратная температура" 1/T часто оказывается более удобной величиной.

Перевернутое ("инверсное") заселение уровней используется в лазерной технике.

Когда уровней только два, температура определяется просто - из логарифма отношения населенностей" Однако если уровней много, то положение усложняется. Далеко не всегда "неправильную" населенность уровней можно описать одним параметром - температурой.

Если можно изменить энергию всех уровней ε на -ε_m, то понятие отрицательной температуры имеет чет-кий смысл. Именно так обстоит дело для энергии спинов в магнитном поле. Мы видели, что если спин атома равен s, то система имеет 2s+1 состояний со значениями энергии, составляющими арифметическую прогрессию. Интервалы между уровнями одинаковы, и замена В на -B изменяет только порядок уровней, не изменяя их расстояния, так что вся схема уровней не деформируется. Именно поэтому мы и рассмотрели пример с магнитным моментом.

Если же схема уровней не так проста и интервалы между уровнями разные, то мы не можем простым образом "перевернуть" населенности уровней и, строго говоря, отрицательная температура для такой системы не имеет смысла. Однако и в этом случае можно говорить о температуре, разной для разных участков спектра уровней, выбирая участок так, чтобы внутри них можно было считать интервалы одинаковыми. В этом случае можно говорить о разных температурах в разных участках спектра. Установление равновесия и здесь состоит в изменении населенности в сторону правильного, равновесного распределения, И опять второе начало термодинамики укажет нам направление тепловых потоков.

Случай неравных интервалов очень распространен в спектрах атомов, где магнитный момент атомов имеет сложную природу, так как создается движением многих электронов и их спинов. Понятие отрицательных температур стало важным понятием в оптике и особенно в физике лазеров.

Для всех рассуждений было очень важно, что система может иметь ограниченный спектр уровней энергии. Только в этом случае у системы кроме самого нижнего уровня есть и самый верхний, и эту систему можно "перевернуть" - заменить Т на -Т и получить картину, отвечающую формально T<0.

Для поступательного движения, для которого энергия может изменяться от 0 до ∞, отрицательные температуры невозможны - для таких систем нельзя создать распределение, отвечающее отрицательным температурам.