Равновесие спинов и температура

Пусть сначала никакого магнитного поля нет. Тогда повороты спинов не влияют на энергию, и спин с одинаковой вероятностью имеет любую из 2s+l проекций. Условно мы изобразим эту картину так, что на каждом из 2s+1 уровней, которые имеют одинаковую энергию, нарисуем одинаковое число кружочков (рис. 27). После включения магнитного поля в первый момент количество атомов на каждом уровне не успеет измениться, хотя энергия уровней станет разной согласно формуле ε_m=-mg μ₀B.

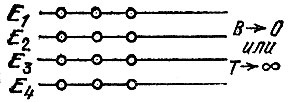
Рис. 27. Распределение атомов без магнитного поля

Если бы атомы были полностью изолированы, то их спины, как свободные магнитные стрелки, не могли бы остановиться - для остановки нужно трение в опоре. Роль трения для атомов будет играть их взаимодействие с другими атомами, с которыми они обмениваются энергией. Это и будет процессом установления теплового равновесия. В результате через некоторое время распределение спинов атомов по уровням будет описываться формулой, похожей на формулу Максвелла, а именно: число атомов, которые будут находиться на т - м уровне и иметь энергию ε_m, пропорционально знакомой уже экспоненте:

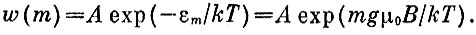
Коэффициент А определяется из условия, что полное число ядер задано и равно, например, N:

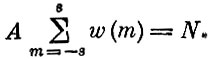
Сумму (она есть геометрическая прогрессия с отношением соседних членов, равным exp(g μ₀B/kT) легко вычислить (мы предоставляем это читателю).

Распределение спинов атомов в тепловом равновесии иллюстрируется на рис. 28.

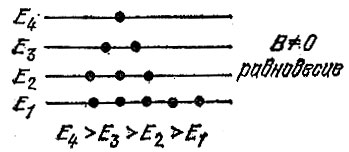
Рис. 28 Спины в магнитном поле и тепловом равновесии

Мы видим, что можно говорить о спиновой температуре атомов. Это Рис. 28. Спины в магнитном есть величина, которая определяет закон распределения спинов по разным проекциям в магнитном поле. Если температура очень велика (Т →0), то экспонента становится равной единице и все ω (m) становятся равными друг другу.

Распределение спинов атомов по уровням в магнитном поле приводит почти сразу к неожиданному парадоксу.