Задача для развлечения

Мы уже много рассказали о температуре и тепловых процессах. Может быть, читатель понял, как нелегко было обнаружить в процессах передачи тепла энтропию и как ее появление в физике преобразило всю науку. Наверно, будет полезным посмотреть на простом примере, как работают в паре температура и энтропия.

Проиллюстрируем понятие энергии в гидродинамике.

Воспользуемся еще раз двумя бассейнами, уровни воды в которых будут разными. Вода может перетекать из одного бассейна в другой. Поставим между бассейнами турбинку, которая, как аккумулятор, будет "собирать" энергию, поднимая, скажем, груз на некоторую высоту. Запасемся еще и насосом, который, если понадобится, будет перекачивать воду обратно. У нас получилась примитивная модель гидростанции. Если потерь на трение нет (так, конечно, не бывает), то легко понять, что вода будет перетекать из одного бассейна в другой до тех пор, пока уровни не выравняются. Потенциальная энергия воды перейдет в потенциальную энергию груза. Если груз опускать, то с помощью насоса можно перекачать всю спущенную воду обратно. Конечно, на самом деле всю воду перекачать не удастся, какие-то потери будут, но ими мы пренебрежем и будем считать нашу установку обратимой.

Если бы турбинки не было, то уровни все равно бы выравнялись, только вся энергия бесполезно превратилась бы в тепло и перекачать воду обратно было бы нечем. Накопив энергию, можно ее использовать для разных целей. Можно, в частности, перекачать воду из третьего бассейна, расположенного еще ниже, в верхний. Короче говоря, можно сделать все, что позволяет закон сохранения энергии.

Построим теперь тепловую машину, по возможности близкую к той, которая была нами описана.

Возьмем три куба, сделанных из одного материала и одинаковых размеров. Пусть кубы нагреты до разной температуры - два до 300 К, а один до 100 К. В дополнение к трем кубам есть еще тепловая машина, которая может работать на любом перепаде температур. До какой максимальной температуры можно нагреть один из кубов?^*

^*( Эта задача предлагалась на экзамене в Кембридже. Она напечатана в книге "Образованный ученый".- М.: Наука, 1979, с, 101, задача 169.)

Возьмем сначала два куба с температурой 100 и 300 К и плотно прижмем их друг к другу. Температуры кубов выравняются. Если для простоты считать, что теплоемкость материала кубов равна единице и не зависит от температуры, то конечная температура окажется равной 200 К, но часть энергии пропадет без всякой пользы. Если подключить тепловую машину, то, по крайней мере, эту часть энергии можно превратить в работу.

Чтобы узнать, какую работу можно получить, надо использовать второе начало. Максимальную работу мы получим, если процесс будет обратимым, т. е. если энтропия всей системы не увеличивается и тем самым выполняется условие

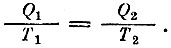
Напомним, что Q₁ есть тепло, отнятое от горячего тела при температуре Т₁ a Q₂ - тепло, отданное холодному телу при температуре T₂. Когда от горячего тела отнималось тепло Q₁, то температура этого тела должна была понизиться на

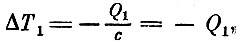
так как теплоемкость с= 1. Точно так же температура холодного тела повысится, когда к нему подводится тепло Q₂, на величину

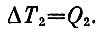
Теперь надо использовать условие обратимости процесса, которое написано выше. Подставим в него выражение для Q₁ и Q₂ и перепишем полученное условие так:

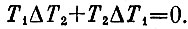
Это условие можно записать и иначе:

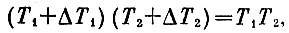
если пренебречь малой величиной ΔT₁*ΔT₂. Такое равенство означает, что, после того как температуры Т₁ и Т₂ в результате обратимого процесса изменились на ΔT₁ и ΔТ₂ (ясно, что ΔТ₁ и ΔТ₂ разных знаков: если Т₁ возрастает, то Т₁ убывает), площадь прямоугольника с длинами сторон Т₁ и Т₁ осталась постоянной:

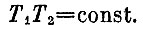
Такому соотношению должны удовлетворять температуры двух кубов в начале и в конце процесса, если процесс обратим.

Теперь у нас есть все, что надо для расчетов. Начнем с того, что построим тепловую машину из двух кубов с T=300 К и 100 К. Когда в обратимом процессе их температуры выравняются, то конечная температура Т определится из соотношения

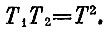
Значит, Т= (300* 100)^1/2≈173 К.

Простое продолжение состояло бы в том, чтобы работу, которая была получена на первом этапе, превратить в тепло и отдать это тепло третьему кубу. Температура его при этом поднялась бы до 354 К.

Это следует из закона сохранения энергии - первого начала термодинамики. Энергия наших кубов равна численно их температуре, так что работа, запасенная на первом этапе, равна

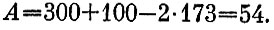
Такое решение, однако, неправильно! Правильный ответ состоит в том, что запасенную работу надо использовать для работы холодильника, охлаждая систему двух кубов с T=173 К и нагревая куб с T=300 К.

Этот новый этап описывается не условием T₁T₂=const, а другим условием:

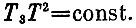
Появление квадрата Т связано с тем, что охлаждение системы кубов описывается условием Q=-2ΔT, т.е.

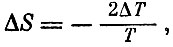
и уравнением Карно

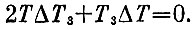
Рассуждая почти так же, как раньше, получим уже написанное условие T₃T²=const. Обозначая конечные температуры через x иy, получаем

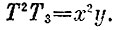
Одного уравнения для вычисления двух температур мало. Второе уравнение дает первое начало:

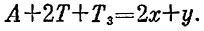
Подставляя значения А, Т и T₃, получаем систему

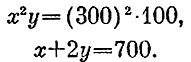
В итоге получим

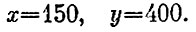
Итак, температуру горячего куба можно довести до 400 К, охладив при этом два других до 150 К.

Другое решение. Все рассуждения можно сделать короче и, главное, почти автоматически, если воспользоваться энтропией. Энтропия для куба, если его теплоемкость постоянна, равна

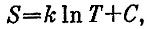
где постоянная С не зависит от температуры^*.

^*( Это выражение мы получали для идеального газа. При выводе использовалось только одно свойство газа - независимость теплоемкости от температуры. Поэтому оно верно и в нашем случае.)

Условие обратимости означает, что энтропия системы, состоящей из трех кубов, не изменяется. Максимальное нагревание одного куба достигается, очевидно, тогда, когда температуры двух других сравниваются (иначе с их помощью можно было бы получить еще работу). Вспоминая, что энтропии кубов складываются, получим

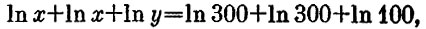
или

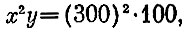
т. е. первое уравнение, которое было получено более длинным путем. Второе уравнение, естественно, остается прежним.

Если еще раз попытаться сравнить задачу о трех кубах с задачей о трех бассейнах, то мы увидим, что роль потенциальной энергии играет логарифм температуры - энтропия - и вместо одного закона сохранения энергии появляются два начала термодинамики: первое определило сумму температур, второе - сумму их логарифмов^*. Главное в задаче о трех кубах - это то, что никакими способами нельзя понизить температуру холодного куба - это запрещает второе начало. В задаче о бассейнах работу, полученную от одной турбины, можно использовать для понижения уровня воды в третьем, самом низком бассейне.

^* ( Условию одинаковой массы кубов в задаче о бассейнах будет отвечать одинаковая площадь бассейнов.)

Сравнить обе задачи очень полезно.

В дополнение ко всему можно еще вспомнить о том, что говорилось о низких температурах. Формула

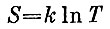
не может быть верной, если температура низкая. Вблизи T=0 энтропия не может стремиться к - ∞, а должна стремиться к нулю, так как любая система при Т=0 находится в упорядоченном состоянии и ее энтропия должна исчезать. Поэтому надо быть внимательным к тому, о каких температурах идет речь. Для температур, которые выбраны были в задаче, все обстоит благополучно.