Фотонный газ

В 1924 г. молодой индийский физик Бозе обнаружил, что распределение Планка можно получить почти таким же образом, как и распределение Максвелла, если считать электромагнитное поле системой из множества фотонов, т. е. считать его идеальным фотонным газом. При этом, конечно, не надо забывать, что фотоны - это не обычные атомы, они не имеют массы покоя. Бозе про это не забыл и обнаружил, что формула распределения Планка есть не что иное, как равновесное распределение такого фотонного газа, названного впоследствии бозе-газом.

Вывод Бозе очень понравился Эйнштейну; он перевел его статью на немецкий язык (с английского) и направил ее в физический журнал^*. После этого электромагнитное поле (поле фотонов) стало примером нового идеального газа, у которого уравнение состояния, конечно, не имеет ничего общего с уравнением Менделеева - Клапейрона.

^* (В то время "главным" журналом был "Zeitschrift fur Pliysik", выходивший в Германии.)

Вывод уравнений состояния фотонного газа более сложный, чем вывод уравнения обычного идеального газа. Но в этом выводе стоит разобраться.

Пока у нас есть формула для плотности энергии излучения Е₀. Если плотность энергии умножить на объем, то получим внутреннюю энергию излучения:

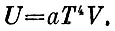
Для того чтобы увеличить энергию на ΔU, надо повысить температуру на некоторую величину ΔТ:

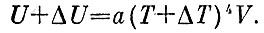
Но

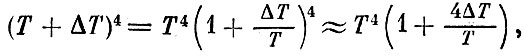
отсюда

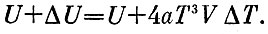
Это значит, что увеличение энергии ΔU связано с увеличением температуры ΔТ соотношением

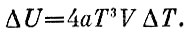
Но увеличение энергии при ΔТ=1 есть теплоемкость системы при постоянном объеме:

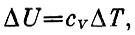
т. е.

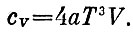
Теперь мы можем сосчитать, насколько изменилась энтропия. Мы знаем, что

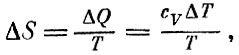
так как тепло, подводимое к фотонному газу, идет на увеличение его внутренней энергии. Итак,

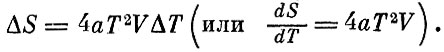
Теперь надо догадаться, как же выглядит формула, которая связывает энтропию и температуру, чтобы изменение энтропии выражалось написанной выше формулой.

Предположим, что формула для энтропии имеет вид

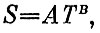
где коэффициенты А и В надо определить. Увеличим S на ΔS, а Т на ΔТ:

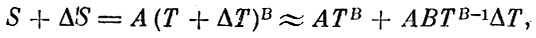
т. е.

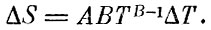
Сравнивая с формулой для ΔS, полученной выше, сразу найдем

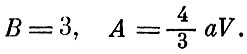
Таким образом, мы нашли выражение для энтропии излучения:

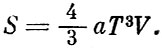
Заметим, что, в согласии с Нернстом, энтропия обращается в нуль при Т=0.

Можно показать, что излучение ведет себя как газ, что его можно сжимать, затрачивая работу, и что при расширении оно само совершает работу. Пусть, например, объем, в котором находится излучение, увеличился от значения V₁ до значения V₂. Если температура при этом поддерживается постоянной и процесс обратимый, то при увеличении объема энтропия возрастет:

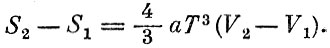
Так как с увеличением энтропии связан подвод тепла: ΔS=ΔQ/T, то

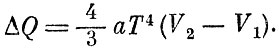
Энергия излучения возрастает при расширении на величину

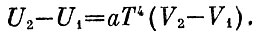
Мы видим, что энергия возросла меньше, чем поступило тепла. Так и должно быть, так как часть тепла пошла на совершение работы. Из последних двух формул находим, что эта работа

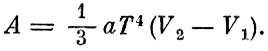
Но она, как известно, равна произведению давления газа на увеличение объема, т. е.

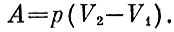
Отсюда получается, что давление излучения равно

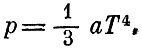
Это и есть уравнение состояния фотонного газа. Сразу видно, что оно резко отличается от уравнения состояния идеального газа. Наиболее удивительно, что давление не зависит от объема, т. е. фотонный газ можно сжимать изотермически и его давление не будет при этом возрастать. Такое поведение может показаться противоречащим здравому смыслу. В этом, однако, нет ничего странного, если вспомнить, что число фотонов не сохраняется. При сжатии газа часть фотонов исчезает, поглощается стенками сосуда; при расширении газа рождаются новые фотоны.

Если энтропию газа поддерживать постоянной, т. е. если совершать с газом адиабатический процесс, то объем и температура будут связаны уравнением адиабаты:

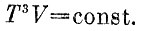
Зная уравнение изотермы и адиабаты, можно проверить теорему Карно, выбрав в качестве рабочего газа фотонный газ. Фотонный газ имеет еще одну особенность: он почти всегда идеальный. Фотоны практически не взаимодействуют друг с другом (не сталкиваются), и поэтому их тепловое равновесие устанавливается только благодаря процессам поглощения и излучения стенками сосуда.

Если бы можно было создать условия для существования равновесного фотонного газа и уметь измерять его давление, то мы имели бы идеальный термометр, который без всяких поправок измерял бы термодинамическую температуру. Это был бы самый точный термометр на свете. К сожалению, повторить опыт Лебедева (измерить давление света) очень трудно, а создать условия теплового равновесия еще труднее. Поэтому фотонный термометр в таком чистом виде создать пока нельзя, хотя принцип фотонного термометра и используется уже давно для оценки температуры звезд. Если бы спектр излучения звезды описывался формулой Стефана - Больцмана, то звезда служила бы термометром, измеряющим свою собственную температуру. Но для этого она должна была бы быть черным телом.