Броуновское движение

Нас не должно удивлять, что в одном объеме могут существовать разные температуры. Потоки тепла (или энтропии) от спинов к решетке, от магнитных облаков к протону и многие другие примеры иллюстрируют процессы установления теплового равновесия, когда тепло передается от более хаотической системы (большие Т) к более упорядоченной (малые Т). Первым примером такого процесса было броуновское движение. Оно было открыто в 1827 г. английским ботаником Р. Броуном, который в своей статье (1828 г.) описал беспорядочное движение маленьких пылинок в жидкости, наблюдаемое в сильный микроскоп.

Интересно, что это явление почти сразу связали с движением молекул жидкости, но потом почему-то эта точка зрения была отвергнута, и даже в начале нашего века броуновское движение стали объяснять потоками в жидкости.

В 1905 г. в Энциклопедическом словаре Брокгауза и Ефрона было написано: "Долгое время многие думали, что явление обусловливается действительным молекулярным движением внутри жидкости. Такого мнения придерживался еще в 1863 г. Винер. Но тотчас же после открытия явления высказывались и другие взгляды на причину его...". Так что от проблемы броуновского движения предпочитали отворачиваться. Поэтому, когда в 1905 г. появилась работа Эйнштейна "О движении взвешенных в покоящейся жидкости частиц", в ней не было даже ссылки на броуновское движение. Теория собственно броуновского движения содержалась лишь в его публикации следующего года.

Суть теории броуновского движения состоит в том, что в тепловом равновесии (в классической кинетической теории газов) все степени свободы следуют на равных основаниях закону равнораспределения.

Пылинки в жидкости образуют систему - идеальный газ частиц, хотя и не взаимодействующих между собой, но взаимодействующих с частицами жидкости, в которой они плавают.

Вообразим себе, что все эти пылинки остаются неподвижными. Это означало бы, что температура "газа" из пылинок была бы равна абсолютному нулю. Тогда неизбежно возникнет поток тепла от жидкости к пылинкам, который не прекратится до тех пор, пока на каждой степени свободы пылинки но накопится энергия, равная 1/2кT. Пылинка будет участвовать в тепловом движении наравне с частицами жидкости.

Рассматривая пылинку - шарик с радиусом r₀, движущуюся в жидкости с коэффициентом вязкости η, Эйнштейн получил формулу для среднего квадрата ее смещения (t - время):

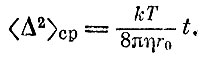
Еще до работы по теории броуновского движения Эйнштейн обратил внимание на то, что из наблюдения явления диффузии, обусловленного движением молекул вещества, растворенного в жидкости, можно определить постоянную Авогадро. Для этого надо найти из опыта к и воспользоваться известным значением газовой постоянной: N_A=R/k. Эйнштейн это и сделал. Полученное им значение N_A=3,3* 10²³ близко совпадало с принятым тогда значением. Расчет Эйнштейна был ярким доказательством реальности молекул, в чем в 1905 г, еще многие сомневались^*.

^* (Полезно отметить, что среднее смещение пылинки - это среднее по времени, вычисленное для одной пылинки. Эйнштейн использовал, как мы знаем, среднее по времени, а не среднее но частицам, как считали в то время в кинетической теории газов. Это позволило ему решить задачу о броуновском движении.)

Из формулы для среднего квадрата смещения мы видим, что, измеряя смещение пылинки, можно определить температуру жидкости. Этот способ должен быть, в принципе, очень обещающим. Пылинки - это идеальный газ. Тепловое равновесие устанавливается быстро. Трудно только точно измерить Δ².

Можно рассмотреть и другие примеры броуновского движения. Например, вместо пылинки можно рассмотреть шарик радиусом r₀, который может не только двигаться поступательно, но и вращаться. Можно вычислить средний квадрат угла поворота шарика вокруг своей оси < θ²>_cp. Эйнштейн дал следующую формулу:

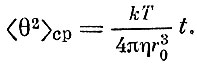
Шарик может служить термометром, причем для измерения отношения температур не надо знать значение к.

Нетрудно получить аналогичную формулу для шарика, который закреплен на невесомой пружинке с коэффициентом упругости а. Приравнивая среднюю потенциальную энергию шарика (как для частицы в газе) обычной величине ?kT

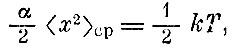
получим для среднего квадрата смещения 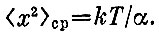Приделайте сбоку от шарика шкалу - и термометр готов!