Флуктуация

Говоря о температуре, энтропии, мы следовали взглядам термодинамиков прошлого века. Предполагалось, что эти величины имеют строго заданное значение в каждой точке и в состоянии теплового равновесия температура и давление строго постоянны по объему. Эти предположения лежали в основе и первого и второго начала термодинамики.

На самом деле, конечно, все величины изменяются со временем и с координатами. Выводя формулу для давления газа на стенку, мы говорили лишь о среднем давлении. Если бы можно было следить за давлением подробнее, измеряя его через каждые τ секунд (где т так мало, что число ударов о стенку за время τ было бы небольшим), то прибор показал бы, что давление все время колеблется, флуктуирует. Так как давление пропорционально плотности энергии в единице объема, то с его изменением изменится также и энергия. Флуктуации энергии (как и других величин) удобно было бы характеризовать отклонением ее величины от средней (ε- ε_cp)_Ср. Но эта величина в среднем равна нулю^*. Поэтому естественно характеризовать флуктуации средним значением квадрата этой величины:

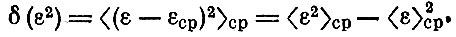
Эта величина называется средней квадратичной флуктуацией. Именно о ней обычно идет речь, когда говорят о флуктуациях. Вычислять флуктуации - дело трудное, и мы приведем только несколько окончательных результатов.

^* (Отклонение в меньшую сторону и отклонение в большую сторону взаимно компенсируются. )

Для флуктуации давления получается формула

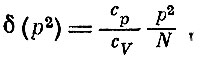
или

где N- число частиц в системе. Это и есть оценка точности самого понятия давления. Так как N обычно очень велико, то флуктуации давления обычно очень малы. Аналогичная формула для флуктуаций температуры одноатомного газа имеет вид

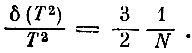
Такие формулы показывают, сколь точны в обычных условиях термодинамические понятия. Обе формулы - для флуктуации давления и для флуктуации температуры - почти совпадают. Обе они утверждают, что точность этих понятий растет, как корень квадратный из числа частиц:

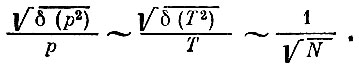
Так, для 1 мм³ газа (при давлении 1020 гектопаскалей) N ∼10¹⁹ и относительные флуктуации составляют примерно 10^-16. Значит, для такого количества газа давление и температура имеют точный смысл.

Но мы начали разговор о флуктуациях не только для обоснования привычных понятий, а для того, чтобы найти способ измерения температуры. Написанные выше формулы ничего нам в этом смысле не добавляют, так как измерять флуктуации термодинамических величин очень трудно. Дело становится несколько проще, если перейти к величинам электрическим.

В электрической цепи, в которой нет э.д.с., ток не идет. По крайней мере, это следует из закона Ома. В действительности это не совсем так. Вернее, это утверждение строго справедливо лишь при абсолютном нуле, когда нет флуктуаций. При других температурах возникает случайный ток, тепловое движение электронов случайно становится упорядоченным.

Величина флуктуаций тока была вычислена Найквистом в 1927 г. Возникающий ток не может быть, естественно, постоянным, а с равной вероятностью возникает ток разной частоты. Вместо тока можно говорить о флуктуационной э.д.с. При частоте ω такой, что ћ ω <<кТ, для полосы частот Δω=1 она определяется формулой

где R(ω) - сопротивление цепи при частоте со. На флуктуационную э.д.с. можно смотреть как на свидетельство тепловых колебаний электромагнитной системы. Полученная формула уже может служить основой для измерения температуры. Однако физики, занимающиеся устройством температурной шкалы, нашли еще лучший метод.

Для того чтобы понять, о чем будет идти речь, надо сначала объяснить, что такое шум, точнее, что такое белый шум.

Вернемся к проводнику, находящемуся при температуре Т. Пусть теперь по нему течет ток, который питает, например, обмотки магнита микрофона; это простейшая схема телефонной линии. Из-за тепловых эффектов на ток, несущий какую-то полезную информацию, наложатся случайные переменные токи, которые будут восприниматься микрофоном и создавать шумовой фон. Такой шум можно представить спектром зависимости интенсивности сигнала от частоты. Если этот спектр отвечает хаотическим помехам, то шум называют белым - белый шум не несет никакой информации, кроме информации о температуре. Шум сопутствует любому электромагнитному явлению. Его не обязательно регистрировать микрофоном и воспринимать как звук. Шумом и, в частности, белым шумом называют флуктуацию любой физической величины. Выбирая разные явления, можно, наконец, найти идеальный (по крайней мере с точки зрения теории) метод измерения температуры.

К сожалению, как всякий современный прецизионный метод, метод измерения шумов имеет сложную теорию, и можно лишь в виде примера сообщить, что, измеряя шумы в так называемом переходе Джозефсона (два сверхпроводника, разделенные тонким слоем изолятора), удалось измерить температуру плавления гелия по термодинамической шкале с точностью до пяти знаков.