Как теряется память?

Мы рассказали о том, как первые представления о столкновениях частиц, превратились в термодинамику и статистическую физику. Но развитие науки не следовало по строго логическому пути. Начало ее основывалось на законах классической механики Ньютона, но вслед за тем в ней появились понятия вероятности и теплового равновесия, которые были для механики чужеродными.

Сыщик из детективного романа восстанавливает траекторию пули, застрявшей в стене. Но никто не может восстановить начальную температуру двух порций газа после того, как установилось тепловое равновесие в их смеси. Системы в классической механике помнят о своей истории; газ, как и любая другая статистическая система, о ней не помнит. Хотя интуитивно оба заключения и кажутся естественными, однако, каким образом они могут сосуществовать в физике, было неясно.

С конца прошлого века математики и физики старались преодолеть логический барьер, стоящий на пути от уравнений движения механики Ньютона к теории Максвелла - Больцмана, оперирующей с вероятностями.

Методы механики позволяют решить с любой точностью задачу о движении частиц, если точно заданы их координаты и скорости в какой-то момент времени t₀. Более того, эту задачу можно решить как для времен t>t₀ ("предсказание"), так и для времен I>t<t₀ ("воспоминание"). Небесная механика умеет как предсказывать движение небесных тел и космических кораблей, так и восстанавливать их движение в прошлом (например, вычислять встречи с кометами или время солнечных затмений, случившихся в древности).

Решить задачу нового типа выпало на долю Максвелла.

Максвелл принял участие в конкурсе, объявленном Лондонским Королевским обществом, на лучшее исследование, посвященное природе колец Сатурна. Необходимо было объяснить стабильность колец, объяснить почему кольца не падают на поверхность планеты или не рассеиваются в космическом пространстве, разваливаясь на куски. Максвелл доказал, что кольца не могут быть сплошными потому, что в сплошном кольце, которое вращается с постоянной скоростью, скорость в каждой его точке должна быть равна первой космической скорости

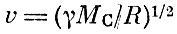
(М_с - масса Сатурна). Скорость обратно пропорциональна корню квадратному из расстояния от центра R, а значит, угловая скорость пропорциональна R^-3/2. Поэтому кольцо не может двигаться с постоянной угловой скоростью, которая не зависит от R, его разорвут центробежные силы.

Но доказав, что кольца не могут быть сплошными, следовало считать, что они состоят из большого числа сравнительно маленьких обломков и для описания их движения естественно использовать вероятностные представления, рассматривая не движение отдельных осколков, а изменения функции распределения.

Когда Максвелл начал изучать поведение газа, он уже был готов с самого начала к тому, что теория должна иметь дело не с поведением отдельных частиц, описываемых уравнениями механики, а их статистическими средними, полученными усреднением физических величин по большому числу частиц или по большому числу столкновений. Для описания поведения систем такого рода Максвелл использовал функцию распределения. Получить эту функцию строго Максвелл не мог; каждый раз приходилось явно или не явно постулировать хаотичный характер движения частиц. Но если не требовать большой строгости, можно написать уравнение, которое описывает, как зависит функция распределения от времени. В простейшей форме такое уравнение называют кинетическим уравнением Больцмана. Уравнения Больцмана заменили в статистической физике уравнения Ньютона. Вместе с ними исчезли и координаты, и скорости отдельных частиц. Если они и появляются (например, в броуновском движении), то они выступают как некоторые средние значения, флуктуирующие под действием теплового движения молекул.

При решении задачи механики обычно задают начальные данные - значения всех координат и скоростей в какой-либо начальный момент времени, тогда решение уравнения Ньютона определяет, как изменяются эти величины со временем. Начальные значения определяют все поведение системы при условии, конечно, что мы точно знаем, какие силы действуют все это время на частицы, как и с чем они взаимодействуют.

Изменение начальных условий изменяет судьбу системы. Начальные данные сохраняются в свойствах системы и могут быть из нее извлечены в любой другой момент времени. Это свойство и называют памятью системы, система запоминает свою начальную историю.

Более того, система содержит и все, что нужно для предсказания ее поведения в будущем, она "знает" свое будущее.

Система, описываемая статистической механикой - такую систему называют стохастической,- памяти лишена. Свойства газа в сосуде не зависят ни от каких начальных условий, ни от формы сосуда, ни от его размеров.

Если не происходит потерь и если газ вращается, то газ сохраняет свою энергию и угловой момент. Однако если у системы есть потери, то даже "память" о его энергии теряется. Так, скорость парашютиста при приземлении никак не связана с его начальной скоростью, сопротивление воздуха поглотило большую часть его кинетической энергии, превратив ее в тепло.

Предположение о стохастичности системы оказывается |(и мы это демонстрировали) полезным при вычислениях.

Принцип хаоса позволяет вывести распределение Больцмана, формулы броуновского движения, потому что в полном хаосе динамику газа можно описывать, как последовательность никак друг с другом не связанных столкновений.

С другой стороны, в модели, в которой газ рассматривается, как набор упруго сталкивающихся шаров, казалось бы, ничто не может стереть память, так как каждое столкновение определяется столкновением предыдущим. Особенно хорошо это видно, если газ находится в сосуде, имеющем форму куба, и его молекулы сталкиваются только со стенками, а угол падения всегда равен углу отражения. Траектории молекул легко могут быть построены, и никакого сходства с хаотическим движением газа возникнуть в такой модели не может.

Ответить на вопрос, в каких условиях возникает стохастичность (хаос), оказалось весьма трудным. Обычная точка зрения связывала хаос с очень большим - в пределе бесконечно большим - числом частиц, которые поело большого числа столкновений заполняют все пространство и принимают все допустимые значения скоростей. Законы вероятностей появлялись, как следствие законов больших систем и достаточно большого времени их развития. Однако реальные физические системы слишком быстро приходят в состояние теплового равновесия, так быстро, как механизм медленной механической эволюции мог обеспечить. Время релаксации - так называют "время забывания" - требовало другого объяснения, другого, хотя бы дополнительного, механизма. Постепенно становилось ясным, что быстрая потеря памяти должна реализоваться и, как оказалось, действительно реализуется в системе с небольшим числом частиц.