Расчётливая поспешность

Мы знаем, что в однородной среде свет распространяется прямолинейно, т. е. скорейшим путём. Но свет движется по кратчайшему пути также и в том случае, когда не идёт от одной точки непосредственно к другой, а достигает её, предварительно отразившись от зеркала.

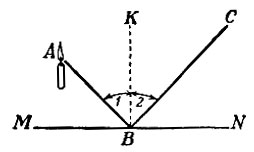
Рис. 108. Угол отражения 2 равен углу падения 1

Проследим за его путём. Пусть буква А на рис. 108 обозначает источник света, линия MN - зеркало, а линия ABC - путь луча от свечи до глаза С. Прямая KB перпендикулярна к MN.

По законам оптики, угол отражения 2 равен углу падения 1. Зная это, легко доказать, что из всех возможных путей от А к С, с попутным достижением зеркала MN, путь ABC - самый скорый. Для этого сравним путь луча ABC с каким-нибудь другим, например, с ADC (рис. 109). Опустим перпендикуляр АЕ из точки А на MN и продолжим его далее до пересечения с продолжением луча ВС в точке F. Соединим также точки F и D. Убедимся прежде всего в равенстве треугольников ABE и ЕВЕ. Они прямоугольные, и у них общий катет ЕВ; кроме того, углы EFB и ЕАВ равны между собой, так как соответственно равны углам 2 и 1. Следовательно, АЕ = EF. Отсюда вытекает равенство прямоугольных треугольников AED и EDF по двум катетам и, следовательно, равенство AD и DF.

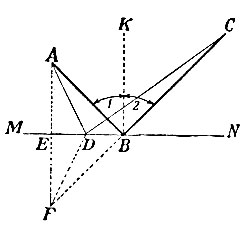
Рис. 109. Свет, отражаясь, движется по кратчайшему пути

Ввиду этого мы можем путь ABC заменить равным 3 ему путём CBF (так как АВ = FB), а путь ADC - путем CDF. Сравнивая же между собой длины CBF и CDF, видим, что прямая линия CBF короче ломаной CDF. Отсюда путь ABC короче ADC,- что и требовалось доказать!

Где бы ни находилась точка D,- путь ABC всегда будет короче пути ADC, если только угол отражения равен углу падения. Значит, свет действительно избирает самый короткий и самый скорый путь из всех возможных между источником, зеркалом и глазом^*.

^* (На это обстоятельство впервые указал ещё Герои Александрийский, греческий механик и математик II века.)