§ 13. Уравнение состояния идеального газа

В предыдущих параграфах мы рассмотрели газовые процессы, в которых один из параметров, характеризующих состояние газа, не менялся. Однако в природе и в технике газовые процессы чаще протекают так, что одновременно меняются все параметры (V, р, t°). Например, при работе газа в цилиндре двигателя внутреннего сгорания одновременно изменяются и температура, и давление, и объем. Выясним, какая существует зависимость между всеми параметрами газа в случае, когда все они одновременно изменяются.

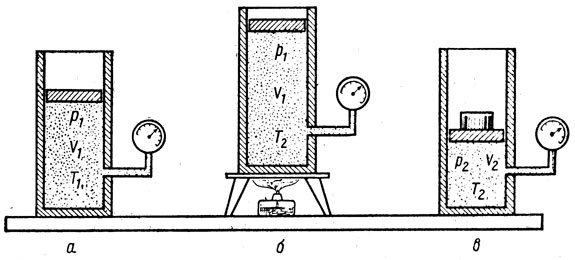
Рис. 14. К выводу формулы объединенного газового закона

Допустим, что в начальном состоянии (рис. 14, а) некоторая масса газа m имеет давление р₁, объем V₁ и температуру Т₁. Оставив давление постоянным (рис. 14, б), нагреем газ до температуры Т₂. Его объем увеличится и станет V' (промежуточное состояние). Переход газа из начального состояния в промежуточное произошел по закону Гей-Люссака:

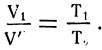
Оставив температуру газа без изменения, уменьшим его объем до V₂ (рис. 14, в), при котором давление стало р₂ (конечное состояние). Переход газа из промежуточного состояния в конечное произошел по закону Бойля-Мариотта:

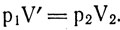
Выразив значения V' из первого и второго равенств:

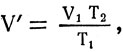
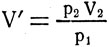
и приравняв их:

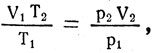
получим

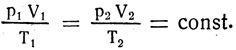
Это уравнение состояния идеального газа, когда все его параметры меняются. Для данной массы газа произведение давления на объем, деленное на абсолютную температуру, есть величина постоянная, как бы параметры состояния газа ни изменялись. В уравнении состояния идеального газа отношение 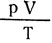для различных масс газа имеет разное численное значение.

Получим данное уравнение для случая, когда масса будет выражена в киломолях. Если брать газа 1 кмоль, тогда при нормальных условиях р, V, Т будут величинами постоянными для любого газа, а именно: р = 1 атм, t° = 0°C или Т = 273°К, объем 1 кмоля V₀ = 22,4 м³. При таком условии и отношение 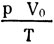будет всегда равно одной и той же величине

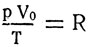
или

R - универсальная газовая постоянная, она одинакова для всех газов. Выясним ее физический смысл:

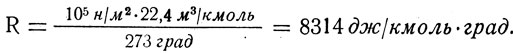
Из наименования видно, что универсальная газовая постоянная равна работе, которую может совершить 1 кмоль идеального газа при его изобарическом нагревании на 1°.

Если при нормальных условиях масса газа будет n кмолей, то ее объем V = V₀n.

Тогда

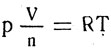
или

Если массу газа m разделить на молекулярную массу μ, получим число кмолей газа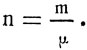

Заменив n, получим уравнение газового состояния:

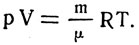
Произведение объема любой массы газа на его давление прямо пропорционально абсолютной температуре. Уравнение состояния идеального газа в таком виде называется уравнением Менделеева - Клапейрона?

Уравнение состояния идеального газа используется, например, при расчете силы тяги, мощности реактивных двигателей, двигателей внутреннего сгорания, паровых двигателей, работающих на перегретом паре.

Задача 3. Сжатый воздух, при помощи которого вытесняется вода из балластных цистерн подводной лодки, находится в баллонах при давлении 1,47*10^7н/_м² и температуре 15°С. Емкость каждого баллона 100 л. Какой объем воды можно вытеснить из цистерн воздухом одного баллона, если вытеснение производится на глубине 30 м при температуре 5° С? Плотность морской воды 1030 ^кг/_м³; атмосферное давление 750 мм рт. ст. Воздухом, оставшимся в баллоне после вытеснения, пренебречь.

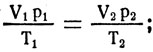
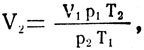
где T₁ = 288° К; Т₂ = 278° К;

р = 750 мм рт. ст.*133 ^н*м-2/_{мм рт. ст.} = 99750 н*м^-2;

p₂ = p + p_в = p + ρgh;

р₂ = 99750 ^н/_м² + 1030 ^кг/_м³*9,8 ^м/_сек²*30 м = 397500 ^н/_м²

Тогда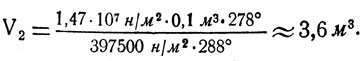

Отв.: V₂ ≈ 3,6 м³.

Задача 4. При атмосферном давлении 760 мм рт. ст. температура воздуха в комнате повысилась с 10 до 25° С. Определить массу вышедшего из комнаты воздуха, если объем комнаты 50 м³. Изменением плотности воздуха пренебречь.

Клапейрона для воздуха до его нагревания и после нагревания:

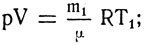
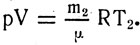
Так как по условию pV остается постоянным, то m₁T₁ = m₂T₂. Отсюда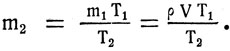

Тогда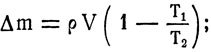

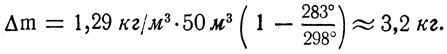
Отв.: Δm ≈ 3,2 кг.