§ 14. Температура - мера средней кинетической энергии поступательного движения молекул

В § 8 указывалось, что температура является мерой средней кинетической энергии поступательного движения молекулы. Используя основное уравнение кинетической теории газа и уравнение состояния идеального газа, докажем математически, что это действительно так.

Помножив и разделив на два правую часть основного уравнения кинетической теории газа

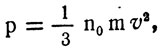
получим

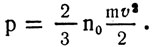
Возьмем киломоль газа Правую и левую части этой формулы помножим на объем 1 кмоля V₀ газа:

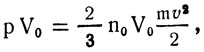
где n₀V₀ = N_A;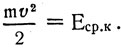 Здесь Е_ср.к - средняя кинетическая энергия поступательного движения одной молекулы газа.

Тогда

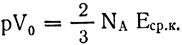
Для одного киломоля уравнение состояния идеального газа:

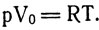
Приравниваем правые части последних двух уравнений:

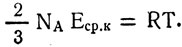
Отсюда

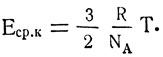
Здесь отношение двух постоянных величин 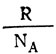есть тоже величина постоянная, она называется постоянной Больцмана (обозначается буквой k):

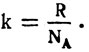
Тогда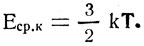

Это формула средней кинетической энергии поступательного движения одной молекулы. Из формулы видно: чем больше кинетическая энергия поступательного движения молекул, тем больше температура тела. Значит, температура характеризует интенсивность теплового движения молекул тела и является мерой средней кинетической энергии поступательного движения его молекул.

Левая часть последней формулы выражает энергию в джоулях, а правая - в градусах температуры. При вычислениях по этой формуле надо, чтобы обе ее части измерялись в одних единицах. Постоянная Больцмана и является переводным коэффициентом, определяющим соотношение между джоулем и градусом.

Вычислим постоянную Больцмана:

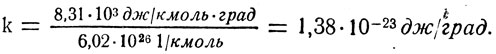
Постоянная Больцмана показывает, насколько изменяется энергия поступательного движения каждой молекулы газа при изменении температуры на 1°.

Задача 5. Определить среднюю скорость движения молекулы азота при 27° С. Молекулярная масса азота 28.

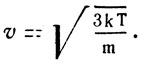
Отсюда искомая скорость

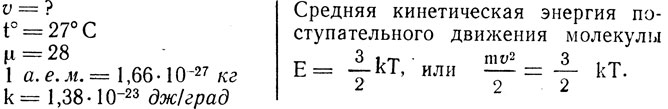
Масса молекулы любого вещества равна атомной единице массы, умноженной на молекулярную массу данного вещества:

Тогда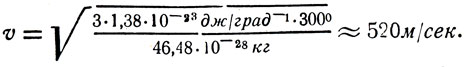

Отв.: v ≈ 520 ^м/_сек.