Физические знания греков

В период нерасчлененной науки физической науки еще не существовало. "Физика" Аристотеля была своеобразной философией природы, собранием некоторых общих идей и понятий "о сущем". Учитель Аристотеля Платон (427-347 гг. до н. э.) считал, что истинная сущность - это сами идеи, а вещи - только несовершенные копии идей. Платоновская "физика" сводилась, таким образом, к некоторым отвлеченным формам и отношениям, постигаемым даже не столько логикой, сколько внутренним созерцанием.

В эллинистический период характер античной науки изменился. Нерасчлененная античная наука стала дифференцироваться, из нее выделились астрономия, механика, математика, медицина. В философии господствовали эпигоны Аристотеля, усиливались идеалистические течения, преобладали этические проблемы. Наука теряла свой общедоступный характер, становилась замкнутой, кастовой, открытой лишь для немногих посвященных. Центром новой науки сделалась Александрия с ее музеем. Здесь была богатая библиотека, велись астрономические наблюдения. Ученых поддерживали египетские цари из династии Птолемеев, основателем которой был полководец Александр Македонский. В эту эпоху большое значение получила математика, а именно геометрия, превратившаяся из прикладной науки об измерении земли в логически строгую дисциплину.

Законченную форму геометрия приобрела у знаменитого александрийского ученого Эвклида (III в. до н. э.). Эвклид положил начало и геометрической оптике, которой посвящены два его трактата: "Оптика" и "Катоптрика". В "Оптике" излагаются основы учения о перспективе, в "Катоптрике" изучаются законы отражения света. Исходным пунктом геометрических построений Эвклида является закон прямолинейного распространения света и закон отражения. При этом Эвклид чертит лучи выходящими из глаза, становясь чисто формально на субъективную точку зрения существования зрительных лучей. Теорию зрительных лучей, с помощью которых глаз как бы ощупывает видимые им предметы, принимали пифагорейцы и Платон. Для формальных построений безразлично, как чертить луч (принцип обратимости луча), поэтому выводы Эвклида сохраняют свое значение, несмотря на неправильность исходной предпосылки. Эвклиду известно фокусирующее действие вогнутых зеркал, однако точного положения фокуса сферического зеркала он не знает. Вогнутые зеркала дают как сходящиеся, так и расходящиеся пучки, выпуклые - только расходящиеся. Фокусирующее действие стеклянных шаров было известно до Эвклида. Эвклид описывает опыт с преломлением света: на дно кубка положено кольцо, глаз помещен так, что кольцо скрыто краями кубка. Не меняя положения глаза, в кубок подливают воду и кольцо становится видимым.

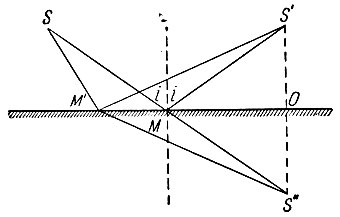
Рис. 1-32. Отражение света, по Герону

Отступая от хронологического порядка изложения, опишем дальнейшие результаты, достигнутые древними в изучении оптических явлений. Герон Александрийский (120 г. до н. э.) показал, что свет, распространяясь от исходной точки до некоторой другой точки, претерпевая отражение от зеркала, проходит путь, требующий наименьшего времени, так что путь SMS', удовлетворяющий закону отражения, меньше другого любого пути SM'S' (рис. 1-32). Клеомед (50 г. н. э.) описывает опыты с преломлением света, в том числе и опыт Эвклида с кольцом, и указывает, что луч света при переходе из менее плотной среды в более плотную приближается к перпендикуляру к границе раздела, восстановленному в точке падения. При обратном переходе луч удаляется от перпендикуляра. Клеомед высказывает мысль, что Солнце при заходе остается видимым вследствие преломления лучей в атмосфере (рефракция).

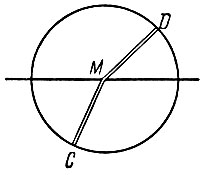
Рис. 1-33. Преломление света, по Птолемею

Замечательный опыт, свидетельствующий, что и в эпоху неразвитого эксперимента древние умели производить точные наблюдения, осуществил знаменитый астроном Клавдий Птолемей (70-147 гг. н. э.). Прибор Птолемея представлял собой диск, в центре которого были укреплены две могущие вращаться линейки DM и СМ. Диск наполовину погружался вводу. Установив линейку DM по определенному направлению, вслед за этим линейку СМ вращали так, чтобы она казалась продолжением DM (рис. 1-33). Измерения углов падения и преломления дали достаточно точные результаты.

Однако Птолемей не нашел точного закона преломления и утверждал, что угол преломления пропорционален углу падения.

Основной кинематической задачей, которую пришлось решать древним, была задача описания видимого движения планет. Эвдокс Книдский (405-355 гг. до н. э.) разработал кинематическую конструкцию из 26 сфер, сочетанием движений которых объяснялось видимое движение планет. Аристотель увеличил число сфер до 56.

Только у Аристарха Самосского (ок. 310-230 гг. до н. э.) мы находим гениальную идею: принять за точку отсчета Солнце. "Он принимает,- писал об Аристархе Архимед,- что Солнце и неподвижные звезды находятся в покое, а Земля движется по кругу около Солнца, помещенного в центре этого круга". Однако учение Аристарха не было поддержано, а сам Аристарх был обвинен в безбожии. Греческие астрономы продолжали разрабатывать геоцентрическую систему. Математик Аполлоний Пергский (ок. 200 г. до н. э.) предложил систему эпициклов для описания движения планет. Планета движется по кругу, называемому эпициклом, центр которого движется по другому кругу - деференту - вокруг Земли, причем для отдельных планет допускалась эксцентричность деферента по отношению к Земле. Знаменитый астроном Гиппарх (160-125 гг. до н. э.), открывший прецессию полярной оси (предварение равноденствий) и составивший звездный каталог из 1022 звезд, также разрабатывал теорию эпициклов. Наконец, Клавдий Птолемей в своем сочинении "Великое построение", получившем большую известность в середине века под арабским названием "Альмагест", детально разработал геоцентрическую систему, с большой точностью согласовывавшуюся с тогдашними наблюдениями. Эта Птолемеева система мира безраздельно господствовала в течение всего средневекового периода.

Развитие астрономии и геометрии шло параллельно. Наконец, математический метод был введен и в механику. Заслуга в этом отношении принадлежала гениальному математику и инженеру древности Архимеду (287-212 гг. до н. э). Архимед происходил из знатной семьи, отец его - Фидий был родственником Сиракузского правителя Гиерона. Сам незаурядный астроном и математик, он дал сыну хорошее воспитание. Архимед изучал Эвклида, был в Александрии и поддерживал постоянную связь с александрийскими астрономами и математиками. Архимед был не только гениальным математиком, но и талантливым конструктором машин и приборов. В частности, он сконструировал автоматическую модель движения небесных светил (планетарий) с водяным двигателем.

Птолемей

Сохранились восторженные рассказы древних историков (Плутарха, Полибия), в которых описывалось, как с помощью своих машин Архимед оборонял Сиракузы во время их осады римлянами. При взятии Сиракуз Архимед был убит, по преданию, во время размышления над геометрическими чертежами, начерченными на песке.

Как математик Архимед прославился тем, что решал труднейшие задачи на вычисление площадей и объемов криволинейных фигур. Эти задачи ныне решаются с помощью интегрального исчисления. Встречающееся в выражении длины и площади круга трансцендентное число я Архимед оценил, указав, что оно заключается между 3 ¹/₇ и 3 ¹⁰/₇₁. Он нашел, что объем конуса, шара, цилиндра одинаковой высоты и одинаковых радиусов оснований относятся, как 1:2:3. Оперируя при решении этих задач с бесконечно малыми элементами, Архимед подходит к идее сосчитать число песчинок, могущих заполнить ограниченную по тогдашним представлениям Вселенную, и находит для этого числа порядок 10⁶³. В вычислениях Архимеда мы находим применение идей атомизма к математике. Начало этому применению было положено Демокритом, с успехом использовавшим математическую атомистику для борьбы с парадоксами Зенона Элейского. Математический атомизм Демокрита и Архимеда был тем зерном, из которого впоследствии развилось исчисление бесконечно малых.

Архимед

В механике заслуга Архимеда состоит в математической обработке начал статики. Многовековой опыт по поднятию и уравновешиванию грузов, по обращению с рычагами привел к эмпирическому выводу закона рычага и представлению о центре тяжести как такой точке, относительно которой уравновешиваются веса всех частей тела. Архимед в своем сочинении "О равновесии плоскостей" решает задачу математического определения центров тяжести плоских фигур. Он доказывает, что центр тяжести треугольника лежит на пересечении его медиан, отсюда он находит центр тяжести четырехугольника, разбивая его на два треугольника, и далее многоугольников и пирамиды. Кроме фигур, ограниченных прямыми линиями, он рассматривает ряд задач о нахождении центров тяжестей криволинейных фигур.

С исследованиями равновесия плоскостей теснейшим образом связана проблема равновесия рычага.

Обоснование закона рычага Архимед дал, исходя из следующих допущений:

1. Равные грузы, действуя на равных расстояниях от точки опоры невесомого стержня, взаимно уравновешиваются.
2. При неравенстве грузов, расположенных на равных расстояниях от точки опоры, перевешивает больший груз.
3. При равных грузах, расположенных на неравных расстояниях от точки опоры перевешивает отдаленный.
4. Действие одного груза может быть заменено действием нескольких равномерно распределенных так, что центр тяжести занимает неизменное положение. Обратно, несколько равномерно распределенных грузов можно заменить одним, подвешенным в их центре тяжести и имеющим вес, равный сумме весов этих грузов.
5. У неравных и подобных фигур центр тяжести расположен подобным образом.

Исходя из этих постулатов, Архимед доказывает закон рычага следующим образом. Пусть грузы А и В соизмеримы между собой и относятся, как целые числа (рис. 1-34):

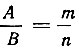
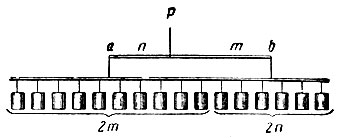
Рис. 1-34. К доказательству закона рычага

Пусть, например, m = 5, n = 3. Делим груз А на 2m = 10 равных частей, груз В на 2n = 6 равных частей и распределим их равномерно вдоль невесомого стержня длиной 2 (m + n) единиц с точкой опоры Р посредине. По постулату 1 грузы будут в равновесии. Равновесие не нарушится, если 2m грузов соединить в один A, приложенный в их центре тяжести а. Но а отстоит от Р на расстоянии Ра = n единиц, а b отстоит от Р на расстоянии Pb = m единиц. Таким образом, уравновешенные грузы А я В удовлетворяют условию:

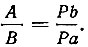
Это и есть закон рычага. Архимед в дальнейшем распространяет его и на случай несоизмеримых грузов.

Логическое обоснование закона рычага нужно было Архимеду прежде всего для чисто математических целей. С помощью принципа рычага он решал сложнейшие задачи геометрии, ныне решаемые методом интегрального исчисления. Методом рычага^* он нашел выражение для объема шара и площадь параболического сегмента.

^* (Ясное изложение метода Архимеда можно найти в книге Д. Пойа "Математика и правоподобные рассуждения" (Изд. иностранной литературы, М., 1957, стр. 183-187.))

Так уже в древности проявляется стимулирующее влияние техники на развитие, казалось бы, такой абстрактной области науки, как математика.

Обратимся теперь к другому результату Архимеда, к его знаменитому закону. Хорошо известен рассказ Витрувия об обстоятельствах открытия этого закона.

Восклицание Архимеда, открывшего закон: "Эврика!" (Нашел!), стало крылатым выражением. Витрувий рассказывает, что Архимед опытом проверил свое открытие. Конечно, не подлежит сомнению, что опыт натолкнул Архимеда на идею и опыт дал ему возможность ее проверить. Более того, Архимед, несомненно, умел на опыте определять удельные веса; упоминают даже о поплавке, с помощью которого сравнивают удельные веса жидкостей (ареометр). Но, верный своему методу, Архимед стремится доказать закон математически, исходя из некоторых постулатов. В основу Архимед кладет следующую гипотезу о природе жидкости:

"Предполагается, что жидкость по природе своей такова, что при равномерном и непрерывном расположении ее частиц менее сдавленная частица вытесняется более сдавленной, и что отдельные частицы этой жидкости испытывают давление отвесно расположенной над ними жидкости, поскольку эта жидкость не замкнута в чем-либо или не испытывает давление со стороны какого-либо другого предмета".

Исходя из этой гипотезы, Архимед доказывает, что поверхность покоящейся жидкости должна быть сферой, центр которой совпадает с центром Земли. В самом деле, если бы этого не было, то не могло бы быть равновесия: одни части жидкости были бы сдавлены больше, чем другие,, что, согласно постулату, привело бы к перемещению менее сдавленных частиц.

Эта теорема у Архимеда играет основную роль. Отсюда он последовательным рассуждением получает свой закон, сформулированный им в следующих предложениях:

"Предложение VI. Твердые тела, которые легче жидкости, будучи погружены в жидкость, стремятся кверху с силой, равной превышению веса жидкости, взятой в объеме этих тел, над весом самих тел.

Предложение VII. Тела, которые тяжелее жидкости, будучи опущены в жидкость, погружаются все глубже пока не достигают дна, и, пребывая в жидкости, теряют в своем весе столько, сколько весит жидкость, взятая в объеме этих тел".

В лице Архимеда механика древних достигла кульминационного пункта. К его результатам последующие авторы не прибавили нового, а в средние века они были утрачены, и Архимедово учение о плавании тел было заменено учением схоластов о том, что плавание тел обусловлено их формой.

В дальнейшем Галилею пришлось восстанавливать в правах Архимеда в спорах со схоластами.

Практика Архимеда, сочетавшего строгую математическую теорию с механическими приложениями, указала путь последующим математикам и инженерам древности, в частности Герону. В связи с этим следует отметить эволюцию во взглядах на механику и изобретения в конце Александрийской эпохи, обусловленную прогрессом техники и процессом разложения рабовладельческого общества. Математик Папп Александрийский, живший в конце III в. или начале IV в. нашей эры. писал:

"Благодаря тому, что механическая наука применяется в жизни и в очень серьезных вещах, она очень высоко ценится философами, а математики занимаются ею с особенным усердием, потому что она раньше всего знакомит нас с учением о природе, материи и элементах мира".

При этом Папп различает теоретическую, или рациональную, механику, которая заключает в себе "геометрию, арифметику, астрономию и физические демонстрации", и практическую, которая "должна обучать искусству бронзовщика, рабочего по железу, строительному и столярному искусству, а также живописи и всему тому, что касается ручного труда".

Папп говорит, что "последователи Герона" указывают, что изучивший хорошо теорию и овладевший ремеслом "будет впоследствии лучшим изобретателем (и конструктором) в области механики".

Таким образом, жизнь ломала рабовладельческие предрассудки, требовала все более конкретных знаний, и математика с философских высот Платона спускалась в обсерваторию астронома и мастерскую конструктора. Жизнь взломала и самый рабовладельческий строй.