Механика

Механика в эпоху научной революции не только продвинулась далее других отраслей естествознания, но и дала научно-методологическую основу всей физике. Идея механического объяснения природы принадлежит Декарту. В своем сочинении "Начала философии", вышедшем в 1644 г., он писал: "Все видоизменения в материи зависят от движения ее частей... во всем мире существует только одна материя... Все свойства, отчетливо различимые в материи, сводятся единственно к тому, что она дробима и подвижна в своих частях и, стало быть, способна к различным расположениям, которые... могут вытекать из движения ее частей"^*. О движении Декарт говорит совершенно определенно, "что оно есть перемещение одной части материи, или одного тела, из соседства тех тел, которые непосредственно его касались и которые мы рассматриваем, как находящиеся в покое, в соседство других тел"^**. Таким образом, это - механическое движение.

^* (Р. Декарт, Избранные произведения, Госполитиздат, 1950, стр. 476.)

^** (Р. Декарт, Избранные произведения, Госполитиздат, 1950, стр. 477.)

В 1687 г. Ньютон в предисловии к своему знаменитому сочинению "Математические начала натуральной философии" писал: "Было бы желательно вывести из начал механики и остальные явления природы... ибо многое заставляет меня предполагать, что все эти явления обусловливаются некоторыми силами, с которыми частицы тел, вследствие причин, покуда неизвестных, или стремятся друг к другу и сцепляются в правильные фигуры, или же взаимно отталкиваются и удаляются друг от друга".

Если сравнить эти два отрывка, то, кроме общего механического подхода к явлениям природы, у обоих авторов нетрудно заметить и различие. Декарт ни слова не говорит о силах, а только о движении. Он не говорит также о частицах или атомах, а говорит только о частях единой материи, которая всегда соприкасается с другими частями той же материи. Другими словами, Декарт мыслит материю как непрерывную сущность, континуум. Все взаимодействия частей материи осуществляются непосредственным контактом этих частей. У Ньютона материя состоит из частичек, которые могут взаимодействовать друге другом на расстоянии посредством дальнодействующих сил. Эти два подхода к механическому объяснению природы получили в дальнейшем название картезианского и ньютонианского. Более подробно о них будет сказано ниже.

Рис. 3-3. Рисунок Леонардо да Винчи, поясняющий направление силы

Понятие силы было выработано в механике не сразу. Древность и средневековье, конечно, имели первичное представление об усилиях, о грузах. Действие рычага состояло в том, что меньшим грузом преодолевалось сопротивление большего груза. Было известно деформирующее действие грузов и мышечного усилия. Леонардо да Винчи чертил расположение натянутых веревок в механизмах, подходя близко к идее графического представления силы. Он правильно понял, что в равноплечем рычаге равные грузы, помещенные на равных расстояниях от оси вращения, не дадут равновесия, если направления, по которым они действуют, наклонены к реальным плечам рычага под разными углами. В связи с этим он вводит понятие потенциального плеча, определяемого перпендикуляром, опущенным из точки опоры на направление силы, и дает правильный ответ на вопрос о равновесии коленчатого рычага. Уяснив значение направления действия силы (рис. 3-3), Леонардо понял, что точку приложения силы, действующей на твердое тело, можно перемещать вдоль линии ее действия без изменения действия. "Где бы ни была привязана веревка nc на протяжении части ас, разницы не будет, ибо она всегда создает линию, которая падает перпендикулярно из центра весов на линию веревки, т. е. линию fm; n - рычаг такой же силы, как а"^*. Леонардо понимал, что ускоренно падающий груз производит иное давление или натяжение, чем покоящийся груз. "Тяжелое тело, опускающееся свободно, не отдает никакой части своей тяжести никакой поддержке". Это положение Леонардо иллюстрирует опытом с равноплечим рычагом, на одном конце которого подвешен груз в 2 единицы, на другом - невесомый блок с перекинутой через него веревкой, несущей грузы 1 и 2. Леонардо ошибочно полагает, что на ось блока будет действовать сила в 2 единицы, на самом деле она будет 2 ²/₃. В другом месте Леонардо рисует блок с перекинутыми через него грузами 1 и 8. "Спрашивается: при опускании 8, поднимающих кверху 1, какую тяжесть ощущает маленький блок cad или ось этого блока?" Он дает ответ, что "ось весов ощущает от обоих грузов тяжесть, равную удвоенному весу меньшего", ибо, по мнению Леонардо, перегрузок падает свободно и не давит. Задача на самом деле решается более сложно, но важно, что Леонардо ее ставит и знает, что ускоренный груз натягивает нить с силой, отличной от силы покоящегося груза. Заметим, что Леонардо уже близко подходит к динамическому определению силы, высказывая ряд правильных утверждений о связи "величины тела" и величины скорости, приобретенной телом за данное время, с действующей силой.

^* (Леонардо да Винчи, Избранные естественнонаучные произведения Изд. АН СССР, 1955, стр. 154.)

Задачу о равновесии коленчатого рычага в общем виде решил Гвидо Убальди (1545-1607). Он сформулировал закон равновесия рычага в виде равенства моментов сил относительно точки опоры. Нахождение закона равновесия рычага имело и то принципиальное значение, что оно позволяло измерять движущую силу в весовых единицах: вес стал эталоном силы.

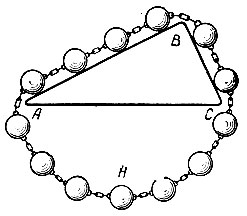
Рис. 3-4. Наклонная плоскость Стевина

Дальнейший шаг в развитии статики был сделан голландским ученым Симоном Стевином (1548-1620). Он рассмотрел равновесие тела на наклонной плоскости (рис. 3-4). Цепь, обвивающая треугольник ABC, не может прийти в движение, иначе получилось бы вечное движение, что Стевин считает невозможным. Поэтому вес длинной части цепи должен действовать так же, как вес ее короткой части, откуда и получается условие равновесия на наклонной плоскости. Вместе с тем Стевин установил, что три силы, направления которых параллельны трем сторонам треугольника, а величина пропорциональна этим сторонам,- уравновешиваются. Так был найден закон сложения сил. Стевину принадлежит также указание, что в блоковых механизмах выигрыш в силе сопровождается проигрышем в пути.

Задачи статики рассматривал также Галилей. Он дал простое и изящное доказательство закона рычага, вывел закон равновесия на наклонной плоскости, опираясь, по существу, на принцип, получивший в дальнейшем название принципа возможных перемещений. Наклонная плоскость играла в исследованиях Галилея по механике очень важную роль, ею он пользовался для проверки открытых им законов падения и для разработки теории маятника. Галилеем было установлено, что скорости, приобретаемые телом при скатывании с наклонной плоскости, не зависят от длины, а только от ее высоты. Опытом с маятником, получившим название маятника Галилея, он доказал, что тело, упавшее с некоторой высоты, поднимается (если не считаться с трением) на ту же высоту, независимо от пути подъема. Таким образом, задача о наклонной плоскости и у Стевина и у Галилея явилась первым примером применения закона сохранения энергии, хотя, конечно, самого закона они еще не знали, а только смутно его предчувствовали. Точно так же у Галилея еще не было ясно осознанной связи между статическим и динамическим понятием силы. При решении задач о движении он пользовался терминами "импето", "момент", включающими в себя и условия действия силы (момент силы в современном смысле), и начальный запас энергии, и иногда силу в современном понимании. Для того чтобы подойти к современному понятию силы, надо было прежде всего освободиться от аристотелевских представлений о движении. Это Галилеем и было сделано.

В своем сочинении "Беседы о двух новых науках", вышедшем в 1638 г., Галилей дает новую, отличную от аристотелевской, классификацию движений, а именно он рассматривает равномерное и неравномерное движения, причем он подробно разбирает равноускоренное движение. Галилей дает следующее определение равномерного движения:

"Движением равномерным, или единообразным, я называю такое, при котором расстояния, проходимые движущимся телом в любые равные промежутки, равны между собою".

При этом Галилей делает очень важное пояснение: "К осуществляемому до сего времени определению (которое назвало движение равномерным просто при равных расстояниях, проходимых в равные промежутки времени) мы прибавили слово "любые", обозначая тем какие угодно равные промежутки времени, так как возможно, что в некоторые определенные промежутки времени будут пройдены равные расстояния, в то время как в равные же, но меньшие части этих промежутков пройденные расстояния не будут равны"^*.

^* (Г. Галилей, Сочинения, т. 1, ГТТИ, 1934, стр. 282-283.)

Так Галилей подготовляет читателя к новому понятию скорости в данный момент. Понимая, что в количественной характеристике движений речь пойдет о переменных величинах, могущих принимать любое значение, он с самого начала представляет прошедшее время и пройденное расстояние отрезками. При переходе к переменному движению встречаются трудности, которые тут же разбираются Галилеем после того, как он дает определение равноускоренного движения: "равномерно, или единообразно, ускоренным движением называется такое, при котором в равные промежутки времени прибавляются и равные моменты скорости"^*. Здесь Галилей употребляет слово "момент" в смысле приращения. Динамическое слово "момент" указывает, что Галилей мыслит некоторый импульс, сообщающий такое приращение.

^* (Г. Галилей, Сочинения, т. 1, ГТТИ, 1934, стр. 293-294.)

Трудность, о которой сейчас же, после проведенного определения, говорит один из участников "Бесед", Сагредо, заключается в усвоении понятия преходящей, переменной скорости. Сагредо так говорит об этой трудности: "...надлежит признать, что для промежутков времени, все более и более близких к моменту выхода тела из состояния покоя, мы придем к столь медленному движению, что при сохранении постоянства скорости тело не пройдет мили ни в час, ни в день, ни в год, ни даже в тысячу лет; даже в большее время оно не продвинется и на толщину пальца - явление, которое весьма трудно себе представить, особенно, когда наши чувства показывают, что тяжелое падающее тело сразу же приобретает большую скорость"^*.

^* (Г. Галилей, Сочинения, т. 1, ГТТИ, 1934, стр. 295.)

Другой собеседник, Сальвиати, представляющий взгляды самого Галилея, разъясняет, что брошенный вверх камень проходит в обратном порядке до остановки все те же ступени медленности, через которые он проходил, падая из состояния покоя. Третий собеседник, Симпличио, представитель официальных аристотелевских взглядов, возражает:

"Но если степени все большей и большей медленности бесчисленны, то они никогда не могут быть все исчерпаны. Таким образом, поднимающийся камень никогда не пришел бы в состояние покоя, но пребывал бы в бесконечном постоянно замедляющемся движении, чего, однако, в действительности никогда не бывает". "Сальвиати: Это случилось бы, синьор Симпличио, если бы тело двигалось с каждою степенью скорости некоторое определенное время; но оно только проходит через эти степени, не задерживаясь более чем на мгновение; а так как в каждом, даже самом малом, промежутке времени содержится бесконечное множество мгновений, то их число является достаточным для соответствия бесконечному множеству уменьшающихся степеней скорости"^*.

^* (Г. Галилей, Сочинения, т. 1, ГТТИ, 1934, стр. 298.)

Эти тонкие рассуждения Галилея показывают, что он ощущал диалектику переменной величины, противоречивый характер движения. Галилей ясно представляет взаимно однозначное соответствие двух бесконечных множеств: "мгновений" и ступеней скорости. В этом же сочинении Галилей устанавливает взаимно однозначное соответствие всех натуральных чисел и их квадратов. Природа бесконечного, бесконечно малых в частности, стала одной из насущнейших проблем математического естествознания.

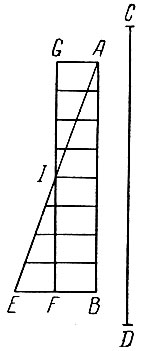
Рис. 3-5. К выводу закона равноускоренного движения Галилея

Пользуясь графическим представлением времен и скоростей (рис. 3-5), Галилей находит закон пути равноускоренного движения 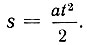Вывод этот хорошо известен из элементарных учебников и является, по существу, одним из первых примеров геометрического интегрирования. Путь s геометрически представляет площадь, ограниченную графиком скорости, осью времени и ординатой, представляющей конечную скорость. Эту площадь Галилей рассматривает как "сумму параллельных линий" - ординат, представляющих графически скорость в данный момент, т. е. мыслит ее вполне в образах интегрального исчисления. Вообще в рассуждениях Галилея о переменном движении ясно чувствуется, как потребность физики заставляла искать новые математические средства, создавать новые математические понятия. Как уже говорилось выше, такие средства были созданы в XVII в. Была создана математика переменных величин и анализ бесконечно малых. Весьма показательно, что Галилей, работая над своими "Беседами", совершенно независимо от Декарта уже, по существу, пользовался методом аналитической геометрии для представления текущих величин. Этой означает, что, когда появляется потребность в научном открытии или изобретении, такие открытия созревают нередко одновременно в нескольких местах, как принято говорить в таких случаях, "идеи носятся в воздухе".

Мы уже говорили, что приращение скорости Галилей назвал "моментом". Закон нарастания скорости в равноускоренном движении таков, что эти "моменты" в любое мгновение одинаковы и не зависят от того, какой скоростью обладает тело в этом мгновение. Здесь скрывается идея независимости действия сил, которая еще раньше со всей отчетливостью была высказана Галилеем в "Диалоге". Но прежде чем перейти к изложению мыслей Галилея о законе независимости действия сил, остановимся на формулировке Галилеем закона инерции. Окончательная формулировка этого закона Галилеем находится в его "Беседах", в беседе четвертого дня.

"Когда тело движется по горизонтальной плоскости, не встречая никакого сопротивления движению, то .. движение его является равномерным и продолжалось бы бесконечно, если бы плоскость простиралась в пространстве без конца"^*. Эта формулировка неудовлетворительна. Во-первых, тело мыслится не свободным, а подверженным действию некоторой связи (движется по плоскости). Во-вторых, ничего не говорится о сохранении направления движения, что может дать повод думать, что Галилей и равномерное круговое движение считает инерционным. Действительно, в "Диалоге" Галилей недвусмысленно говорит, что такой плоскостью без начала и конца, по которой тело будет двигаться равномерно неограниченно долго, будет гладкая сферическая поверхность с центром в центре Земли. Инерционный, лучше сказать, консервативный, характер кругового движения, по мнению Галилея, подтверждается устойчивостью солнечной системы. Галилей также постулирует устойчивость планетных орбит, как в XX в. Бор вынужден был постулировать устойчивость определенных атомных орбит. Для Галилея, как и позднее для Бора, эта устойчивость орбитального движения была основным фактом, носящим характер закона. С другой стороны, несомненно, что Галилей,как и Коперник, находился еще во власти древней традиции, считавшей круг за нечто чудесное и совершенное, и, по-видимому, этим объясняется непринятие Галилеем Кеплеровых эллиптических орбит с их неравномерностью, которую надо было как-то объяснить. До открытия закона тяготения постулат устойчивых круговых орбит явился естественным выходом и ответом на вопрос: что "держит" планеты, в частности Землю.

^* (Г. Галилей, Сочинения, т. 1, ГТТИ, 1934, стр. 417-418.)

Но в "Беседах" чувствуется, что Галилей уже отходит от этой позиции и приближается к правильному взгляду на характер инерционного движения. "Земная" механика,, которой он занимается в "Беседах", подводит его к правильному выводу о движении тела, брошенного горизонтально.

"Если же плоскость конечна и расположена высоко, то тело, имеющее вес, достигнув конца плоскости, продолжает двигаться далее таким образом, что к его равномерному беспрепятственному движению присоединяется другое, вызываемое силою тяжести, благодаря чему возникает сложное движение, слагающееся из равномерного горизонтального и естественно ускоренного движений"^*. Здесь уже ясно видно, что инерционное движение - это равномерное прямолинейное движение (в данном случае горизонтальное). Галилей правильно, применяя принцип независимости действия силы, решает вопрос о форме траектории этого сложного движения:

^* (Г. Галилей, Сочинения, т. 1, ГТТИ, 1934, стр. 418.)

"При сложном движении, слагающемся из равномерного горизонтального и естественно ускоренного движений, бросаемое тело описывает полупараболу"^* (т. е. половину ветви параболы).

^* (Г. Галилей, Сочинения, т. 1, ГТТИ, 1934, стр. 418.)

Одного этого вывода достаточно, чтобы считать Галилея автором закона инерции, хотя он и не дал его полной формулировки. Очень существенно, что, решив в этом предложении задачу внешней баллистики,- определить форму траектории вылетевшего из орудия снаряда,- Галилей ясно указывает, что задача идеализирована, что действительное движение осложняется рядом обстоятельств, и прежде всего сопротивлением воздуха, которое "настолько разнообразно в отдельных случаях, что подвести его под одно твердое правило или научный закон почти невозможно"^*. Поэтому "для научного трактования этого предмета необходимо сперва сделать отвлеченные выводы, а сделав их, проверить и подтвердить найденное на практике в тех пределах, которые допускаются опытом. Польза от этого будет немалая"^**. Это очень важное методологическое указание Галилея, которым и по сей день руководствуется теоретическая физика.

^* (Г. Галилей, Сочинения, т. 1, ГТТИ, 1934, стр. 430.)

^** (Г. Галилей, Сочинения, т. 1, ГТТИ, 1934, стр. 431.)

Сложение движений Галилей рассматривает геометрически.

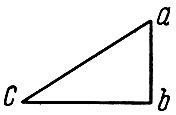
Рис. 3-6. Сложение движений, по Галилею

"Пусть какое-либо тело движется равномерно двойственным образом, и пусть движению его в вертикальном направлении соответствует отрезок ab, движению же в горизонтальном направлении за то же время соответствует отрезок bс. Так как за одно и то же время равномерно движущимся телом проходятся пространства аb и bc, то моменты движения относятся между собой, как ab к bс. Поэтому под действием обоих движений тело пройдет диагональ ас и момент скорости его будет равен ас"^*.

^* (Г. Галилей, Сочинения, т. 1, ГТТИ, 1934, стр. 438-439.)

Приведем еще высказывания Галилея по поводу суперпозиции движений. В "Диалоге" Сагредо говорит:

"... если бы на вершине башни находилась пушка, поставленная горизонтально, и из нее производились выстрелы параллельно горизонту, то в зависимости от большего или меньшего заряда ядро до своего падения пролетело бы тысячу локтей, или четыре тысячи, или шесть тысяч, или, наконец, десять тысяч и т. д., и все же полеты совершались бы в промежутки времени, равные друг другу, и каждый из них равнялся бы тому времени, которое ядро потратило бы на прохождение от жерла пушки до земли, если бы оно упало оттуда без всякого другого импульса вниз по перпендикуляру"^*. Правда, в "Диалоге" Галилей еще неточно считает траекторию снаряда круговой, но в "Беседах" эта ошибка им исправлена.

^* (Галилео Галилей, Диалог о двух системах мира, Гостехиздат, 1948, стр. 124-125.)

Из других результатов, полученных Галилеем в механике, укажем на его подробный разбор движения тела по наклонной плоскости, в частности определение времени скатывания в*зависимости от наклона и длины. Галилей, рассматривая линии скатывания между двумя горизонталями, находит, что время падения по хорде будет больше, чем время падения по ломаной, вписанной в дугу окружности, а время скатывания по этой дуге будет еще меньше. Галилей, правда, не нашел вида линии кратчайшего скатывания (брахистохроны), но совершенно правильно установил, что время скатывания по дуге окружности меньше времени скатывания по хорде и любой ломаной, вписанной в эту хорду. С этим утверждением Галилея связано и другое, что дуга окружности является таутохроной, т. е. время падения тяжелой точки по дуге окружности к ее низшей точке одинаково для различных отрезков этой дуги. Это утверждение выведено из наблюдений изохронности качаний кругового маятника. На самом деле оно правильно только для малых дуг. Время качания маятника Галилей нашел пропорциональным корню квадратному из его длины.

Итак, Галилей получил в области механики следующие результаты:

1. открыл закон инерции, хотя и не дал его полной и точной формулировки;
2. открыл принцип суперпозиции движений, установил правило параллелограмма скоростей, нашел траекторию тела, брошенного горизонтально;
3. открыл закон равноускоренного движения;
4. установил принцип относительности для механических процессов;
5. дал основы теории движения кругового маятника и разобрал теорию движения по наклонной плоскости.

Эти, а также ряд других частных результатов, полученных Галилеем, дают полное основание считать его основателем механики. Вместе с тем следует отметить, что такие фундаментальные понятия механики, как масса I и сила, Галилеем еще не определены.

Ученик Галилея, Торричелли, в 1641-1644 гг. рассмотрел задачу о движении тела, брошенного под углом к горизонту, дал метод построения касательной к траектории движения, определил условие наибольшей дальности полета, показал, что огибающей всех траекторий полета, имеющих одинаковую величину, но разные направления скорости, будет парабола.

В 1644 г. Декарт дает полную формулировку закона инерции:

"...тело, раз начав двигаться, продолжает это движение и никогда само собою не остановится"^*.

^* (Р. Декарт, Избранные произведения, Госполитиздат, 1950, стр. 486.)

"Второй закон, замеченный мною в природе, таков: каждая частица материи в отдельности стремится продолжать дальнейшее движение не по кривой, а исключительно по прямой, хотя некоторые из этих частиц часто бывают вынуждены от нее отклоняться, встречаясь на своем пути с иными частицами..."^*.

^* (Р. Декарт, Избранные произведения, Госполитиздат, 1950, стр. 487.)

Обратим внимание, что в этих законах ни слова не говорится о каких-либо причинах или силах, речь идет только о взаимодействии частей материи. Такая постановка вопроса вытекает из общей физической концепции Декарта, который мыслит всю Вселенную как однородную материю, тождественную с пространством. Основным свойством материи Декарт считает протяженность, поэтому количество материи у него тождественно с объемом, ею занимаемым.

Следует заметить, что основные законы движения Декарта изложены им ранее более ясно и четко в сочинении "Трактат о свете", или "Мир", которое он отказался издавать, узнав об осуждении Галилея, и оно было издано только после его смерти в 1664 г. Приведем формулировку принципов, или "правил", Декарта из этого трактата.

"Первое правило заключается в следующем: каждая частица материи в отдельности продолжает находиться в одном и том же состоянии до тех пор, пока столкновение с другими частицами не вынуждает ее изменить это состояние". В частности, величина и форма частицы остаются неизменными, пока удары о другие частицы не деформируют или не раздробят ее; "если, она остановилась на каком-нибудь месте, она никогда не двинется отсюда, пока другие ее не вытолкнут; и раз уж она начала двигаться, то будет продолжать это движение постоянно с равной силой до тех пор, пока другие ее не остановят или не замедлят ее движения"^*.

^* (Р. Декарт, Избранные произведения, Госполитиздат, 1950, стр. 198.)

"В качестве второго правила я предполагаю следующее: если одно тело сталкивается с другим, оно не может сообщить ему никакого другого движения, кроме того, которое потеряет во время этого столкновения, как не может и отнять у него больше, чем одновременно приобрести себе"^*.

^* (Р. Декарт, Избранные произведения, Госполитиздат, 1950, стр. 200.)

Здесь мы встречаемся с первой в новой физике формулировкой закона сохранения движения. Декарт, апеллируя к неизменности бога и его действий, считает, что содержанием двух правил является сохранение богом вложенного им во Вселенную определенного количества движения. Эта апелляция к богу является характерной маскировкой для Декарта, она особенно часто встречается в "Началах философии", но уже современникам Декарта было ясно, что бог здесь является ненужным привеском.

"В виде третьего правила я прибавлю, что хотя при движении тела путь чаще всего представляется в форме кривой линии и что хотя невозможно произвести, как это было сказано, ни одного движения, которое не было бы в каком-либо виде круговым, тем не менее каждая из частиц тела по отдельности всегда стремится продолжать его по прямой линии"^*.

^* (Р. Декарт, Избранные произведения, Госполитиздат, 1950, стр. 202.)

Таким образом, в принципах Декарта закон инерции является частным случаем общего закона сохранения движения. С этими законами связана и мера движения: изолированное тело стремится сохранить свою величину и скорость, следовательно, мера движения, или, как выражался Декарт, сила продолжать свое движение определяется величиной тела, скоростью движения и, кроме того, формой поверхности и способом воздействия различных тел. Чтобы определить эту меру, Декарт рассматривает удар тел. Два равновеликих тела, движущихся по одной прямой с равными и противоположными скоростями, обмениваются скоростями, они ничего не теряют и не приобретают в величине движения. Из этого первого закона удара, установленного Декартом, следует, что в качестве меры движения он принимает величину, названную впоследствии количеством движения, т. е. произведение массы на скорость. Масса у Декарта - это количество материи, равное объему тела при неизменной плотности. Что же касается способности тела сохранять свое движение, т. е. того, что мы называем инертностью, то она определяется не только количеством материи, но и формой тела и его скоростью. Декарт считает, что чем больше скорость тела, тем труднее оно изменяет свое состояние, тем больше его инертность.

Механическая физика Декарта содержала много интересных идей о происхождении солнечных систем (Декарт принимал, что, кроме нашей системы, существуют и другие аналогичные ей миры), о движении планет, о природе тяготения и т. д. В этих построениях Декарта большую роль играли вихревые движения частиц, к которым он пытался свести в конечном счете и силу тяготения. Построения Декарта нередко носили фантастический характер и подвергались резкой критике со стороны Ньютона и его последователей, но они имели то историческое значение, что представляли собой попытку дать последовательную механическую картину мира, основанную на двух основных понятиях: материи и движении - и принципе сохранения материи и движения. Самое картезианское представление о мире, как вечно движущемся материальном континууме, было глубоко прогрессивным и продолжает жить в измененной форме в научных теориях вплоть до наших дней.

Не следует думать, что в своей механике Декарт занимался только общими проблемами и чуждался конкретных задач. Он вновь подтверждает закон параллелограмма скоростей, занимается проблемой удара (хотя и не вполне удачно, ибо Декарт не считал количество движения векторной величиной, к тому же ряд "правил", установленных им, явно противоречит опыту) и проблемой маятника. Декарт первым показал, что задача определения периода колебания физического маятника сводится к определению длины соответствующего математического маятника и, следовательно, к нахождению особой точки: центра качания. Он определил положение центра качания для некоторых плоских фигур. Однако решение задачи о физическом маятнике удалось довести до конца выдающемуся ученому второй половины XVII в. Христиану Гюйгенсу.

Христиан Гюйгенс

Христиан Гюйгенс (1629-1695) был продолжателем Галилея в механике и последователем Декарта в своих физических воззрениях. Его знаменитое сочинение "Маятниковые часы" вышло в 1673 г. В первой части этого сочинения описаны изобретенные Гюйгенсом часы с маятником. Вторая часть посвящена теоретическим вопросам. Здесь, как пишет Гюйгенс, "потребовалось укрепить и, где нужно, дополнить учение великого Галилея о падении тел"^*. Этой части предпосланы ""гипотезы", представляющие собой не что иное, как закон инерции и принцип суперпозиции.

^* (X. Гюйгенс, Три мемуара по механике, Изд. АН СССР, 1951, стр. 10.)

"I. Если бы веса не было и воздух не сопротивлялся движению тел, то каждое из них продолжало бы достигнутое движение прямолинейно и с постоянной скоростью.

II. Однако благодаря действию веса, причину которого мы не рассматриваем, случается, что тела производят сложное движение, составленное из равномерного движения в том или ином направлении и из движения, вызванного весом и направленного по вертикали вниз.

III. Эти два движения можно рассматривать отдельно, и каждое из них не влияет на первое"^*.

^* (X. Гюйгенс, Три мемуара по механике, Изд. АН СССР, 1951, стр. 34.)

Заметим, что формулировка закона инерции опять-таки отличается от современной упоминанием о весе. Мы теперь привыкли отвлекаться от силы тяжести и продолжаем упоминать только о сопротивлении, демонстрируя инерцию. Основатели механики хорошо сознавали, что они живут на Земле, в условиях действия земного поля тяготения, производящего "естественные" движения. Надо было привыкнуть и к мысли о необходимости переноса системы отсчета с Земли на Солнце при решении астрономических задач и к необходимости отвлечься от поля тяготения при решении задач механики в лабораторной системе отсчета. Это было не так-то легко, и об этом надо было напоминать.

За этими гипотезами идут предложения, касающиеся законов падения и движения по наклонной плоскости. Здесь Гюйгенс дает геометрические доказательства выводов Галилея. Через всю цепь доказательств различных случаев красной чертой проходит одна важная мысль: по какому бы пути ни падало тело в поле тяжести, его скорость всегда определяется высотой падения и тело не может подняться на высоту большую той, с которой оно упало, или той, которая соответствует начальной скорости бросания. Другими словами, Гюйгенс доказывает консервативный характер силы тяжести. Все его доказательства, если перевести их на современный язык, представляют собой закон сохранения энергии в механике: сумма кинетической и потенциальной энергии есть величина постоянная.

В итоге своих доказательств Гюйгенс приходит к важному для его'теории часов выводу, что таутохроной является не дуга окружности (как думал Галилей), а дуга циклоиды. Полупериод колебания по циклоиде определяется формулой:

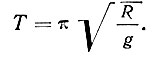
Гюйгенс применяет в своих часах циклоидальный маятник. Для изготовления такого маятника ему понадобилось создать теорию развертки кривых, которой и посвящена третья часть его сочинения.

Четвертая часть книги Гюйгенса посвящена проблеме физического маятника. Этой проблемой Гюйгенс начал заниматься с 1646 г., "когда я был еще почти мальчиком", как он сам пишет, в связи с задачей о центре качания, предложенной ученым монахом Мерсенном.

Книга начинается с определений, из которых мы приведем определения физического и математического маятника и центра качаний.

"Под маятником мы будем понимать любую обладающую весом фигуру (линию, плоскость или тело), так подвешенную, что она может совершать колебательное движение вокруг некоторой точки или, вернее, вокруг горизонтальной оси".

"Под простым маятником мы будем понимать нить или линию, не гнущуюся и невесомую и несущую на нижнем конце прикрепленный груз. Вес этого груза как бы сосредоточен в одной точке".

"Под сложным маятником мы будем понимать тело, состоящее из нескольких грузов, сохраняющих неизменное расстояние как друг от друга, так и от оси колебаний. Таким образом, всякое подвешенное тяжелое тело может быть названо сложным маятником, так как оно может быть мысленно разделено на любое число частей".

"Центром качаний любой фигуры назовем ту точку оси фигуры, расстояние от которой до оси колебаний равно длине простого маятника, изохронного с подвешенной фигурой"^*.

^* (X. Гюйгенс, Три мемуара по механике, Изд. АН СССР, 1951, стр. 120-122.)

Эти точные и ясные определения показывают, как далеко со времени Галилея и Декарта продвинулось искусство формулировки проблемы, умение создавать научные обобщения. Сложную задачу - изучение физического маятника - Гюйгенс сводит к изучению системы математических маятников, впервые тем самым переходя от механики точки к механике неизменяемой системы. Руководящим принципом при решении этой сложной задачи у Гюйгенса служит следующая "гипотеза":

"Если любое число весомых тел приходит в движение благодаря их тяжести, то общий центр тяжести этих тел не может подняться выше, чем он был в начале движения"^*.

^* (X. Гюйгенс, Три мемуара по механике, Изд. АН СССР, 1951, стр. 122.)

Другими словами, Гюйгенс опирается на принцип сохранения энергии в механике. Исследование Гюйгенса является важной вехой на пути установления закона сохранения и превращения энергии. Из этого принципа следует, что в отсутствии сопротивления "центр тяжести колеблющегося маятника при спуске и подъеме пробегает одинаковые дуги"^*. Применяя этот принцип к маятнику, Гюйгенс сначала доказывает следующее предложение:

^* (X. Гюйгенс, Три мемуара по механике, Изд. АН СССР, 1951, стр. 125.)

"Маятник, состоящий из нескольких частей, выводят из положения равновесия и затем опускают. Маятник приходит в колебание, начинающееся с состояния покоя. Представим себе, что у маятника, после того как он совершит некоторую часть колебания, исчезнет связь частей между собой и каждая часть направляется вверх с приобретенной ею скоростью и поднимается насколько может; тогда общий центр тяжести всех частей достигнет опять той высоты, на которой был до начала колебания"^*.

^* (X. Гюйгенс, Три мемуара по механике, Изд. АН СССР, 1951, стр. 128.)

После этого задача решается в виде следующего предложения:

"Дан маятник, состоящий из произвольного числа частей; множат вес каждой части на квадрат ее расстояния от оси колебаний. Если сумму этих произведений разделить на произведение, получающееся от умножения общего веса всех частей на расстояние общего центра тяжести от той же оси колебаний, то получается длина простого маятника, изохронного с данным сложным маятником, или расстояние между осью колебаний и центром качаний сложного маятника"^*.

^* (X. Гюйгенс, Три мемуара по механике, Изд. АН СССР, 1951, стр. 130)

Выразим это фундаментальное предложение формулой. Пусть m₁, m₂, m₃ ... будут массы отдельных точек маятника, r₁, r₂, r₃ ... - их расстояния от оси колебаний, а - расстояние центра тяжести от той же оси, P = g∑m_i - общий вес маятника. Тогда приведенная длина выразится формулой:

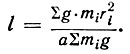
Несколько ранее Гюйгенсом было показано, что

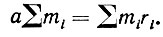
Так что

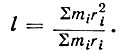
Здесь впервые в истории физики появляется важная величина - момент инерции I_i = ∑mr²_i. Если ввести эту величину и общую массу маятника М = ∑m₃, то формула приведенной длины принимает хорошо известный из учебников вид:

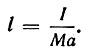
Гюйгенс доказывает в дальнейшем принцип оборотного маятника: "Центр качаний и подвес (ось колебаний) можно поменять местами"^*. Он вычисляет приведенные длины для маятников различных геометрических форм и приходит к выводу, что такой длиной можно воспользоваться в качестве основной линейной меры, приняв в качестве меры длины длину секундного маятника. Хотя Гюйгенс и построил свои часы с циклоидальным маятником, он совершенно справедливо указывает, что для таких измерений можно пользоваться и круговым маятником с малым размахом колебаний, "так как при малых колебаниях, в 5-6 градусов, период колебаний еще достаточно постоянен"^**.

^* (X. Гюйгенс, Три мемуара по механике, Изд. АН СССР, 1951, стр. 163)

^** (X. Гюйгенс, Три мемуара по механике, Изд. АН СССР, 1951, стр. 198)

В заключительной части своего сочинения Гюйгенс приводит без доказательства теоремы о центробежной силе. В этих теоремах содержится известный закон центробежной силы:

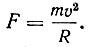
Закон дается без доказательства. Без доказательства даются теоремы, относящиеся к движению конического маятника, и дополнительная теорема, утверждающая, что натяжение нити математического маятника, отклоненного на 90°, в момент прохождения низшей точки равно утроенному весу. Доказательства этих теорем и прежде всего основной формулы для центробежной силы даны Гюйгенсом в мемуаре "О центробежной силе", опубликованном уже после его смерти в 1703 г. В этом же году был напечатан и мемуар Гюйгенса "О движении тел под влиянием удара". Задачу об упругом ударе Гюйгенс решил в 1669 г., однако его результаты не были опубликованы Лондонским королевским обществом, куда он их направил. При решении задачи об ударе Гюйгенс пользуется понятием количества движения. Его он определяет совершенно в духе Декарта: "Количество движения оценивается таким образом, что у неодинаковых тел, движущихся с одинаковой скоростью, количество движения тем больше, чем больше тело. У одинаковых тел, движущихся с разными скоростями, количество движения тем больше, чем больше скорость"^*. Как видим, у Гюйгенса вместо массы фигурирует "величина тела". Для однородной материи она пропорциональна объему, или же, как писал Гюйгенс в 1669 г., "величина тел определяется их весом"^**. Существенно, что Гюйгенс в своих выводах широко опирается на принцип относительности, который он в мемуаре об ударе тел формулирует следующим образом:

^* (X. Гюйгенс, Три мемуара по механике, Изд. АН СССР, 1951, стр. 223.)

^** (X. Гюйгенс, Три мемуара по механике, Изд. АН СССР, 1951, стр. 367.)

"Движение тел, а также их одинаковые или разные скорости надо рассматривать как относительные по отношению к другим телам, которые мы считаем покоящимися, не учитывая того, что как те, так и другие тела могут участвовать в другом, общем движении. Поэтому два тела, соударяясь, даже в случае, если оба вместе участвуют еще в другом равномерном движении, для лица, также участвующего в общем движении, действуют друг на друга так, как будто бы этого общего движения не существовало"^*.

^* (X. Гюйгенс, Три мемуара по механике, Изд. АН СССР, 1951, стр. 213-214.)

Можно констатировать, что в основе механических исследований Гюйгенса лежат два фундаментальных принципа: принцип сохранения энергии и принцип относительности. В этом отношении дух трактатов Гюйгенса напоминает современные работы по теоретической физике. Следует, однако, отметить, что математический аппарат, используемый Гюйгенсом, не соответствует новым идеям. Методами анализа и аналитической геометрии Гюйгенс не пользуется. Примеру Гюйгенса следует и Ньютон, утяжеливший свои "Математические начала натуральной философии" геометрическими доказательствами.

Исаак Ньютон

Исаак Ньютон (1643-1727) завершил дело создания классической механики. Знаменитое его сочинение "Математические начала натуральной философии" вышло в 1687 г., 2-е издание - в 1703 г. Во вступительной части этой книги Ньютон анализирует основные понятия механики: массу, количество движения, силу и, наконец, пространство и время. Сочинение открывается рядом определений этих основных понятий.

"Определение I: Количество материи есть ее мера, возникающая совместно из ее плотности и объема".^*

^* (Перевод В. Г. Фридмана, Успехи физических наук, Гостехиздат, 1957, т. LXI, вып. 3, стр. 452.)

В пояснении к определению Ньютон указывает: "Это же количество я обычно подразумеваю в дальнейшем под названиями тело или масса". Наряду с этими терминами Ньютон употреблял термины: материя, сфера, запас материи, величина, сила инерции. Все это указывает на трудности физического определения такого понятия, как "количество вещества". Для однородной материи оно пропорционально объему, для разнородных веществ необходимо указывать критерий, по которому сравниваются "количества материи". Ньютон в пояснении к этому определению в качестве такого критерия указывает вес, считая количество материи пропорциональным весу, "что мною найдено опытами над маятниками, произведенными точнейшим образом". Следовательно, в этом своем первом определении Ньютон недалеко уходит от Гюйгенса. Фактически он, как и его предшественники, опирается на многовековой опыт человечества в количественном сравнении различных веществ по весу.

В определении II Ньютон определяет количество движения как величину, устанавливаемую пропорционально количеству материи и скорости, и добавляет, что "количество движения целого есть сумма количеств движения его частей".

Понятие количества вещества имеет метафизический оттенок, пока не указаны способы его измерения. Вес - это внешнее действие на материю, переменное по своему характеру, и потому не может быть отождествлен с тем неизменным атрибутом тела, каким, по Ньютону, является масса. В чем же проявляется масса тела? Ответом на этот вопрос является следующее определение:

"Определение III. Врожденная сила материи есть присущая ей способность сопротивления, по которой всякое отдельно взятое тело, поскольку оно предоставлено самому себе, удерживает свое состояние покоя или равномерного прямолинейного движения". "Эта сила,- добавляет Ньютон,- всегда пропорциональна массе, и если отличается от инерции массы, то разве только воззрением на нее".

Вот здесь-то и вводится обычное определение массы как меры инерции. Инерция тела проявляется двояко - как сопротивление и как напор. "Как сопротивление - поскольку тело противится действующей на него силе, стремясь сохранить свое состояние; как напор - поскольку то же тело, с трудом уступая силе сопротивляющегося ему препятствия, стремится изменить состояние этого препятствия". Инерция является изначальным неизменным атрибутом материи, ее "врожденной силой", поэтому ее вполне можно отождествить количеством вещества. Пропорциональность ее весу является случайным, необъяснимым обстоятельством.

Так обстоит дело у Ньютона с понятием массы. Последующие определения посвящены уточнению понятия силы.

Определив силу - определение IV - как "действие, производимое над телом, чтобы изменить его состояние покоя или равномерного прямолинейного движения", Ньютон указывает на внешний по отношению к телу характер этого действия. Сила может быть произведена ударом, давлением и, наконец, некоторым силовым центром. Это последнее действие Ньютон считает необходимым определить полнее и точнее.

"Определение V. Центростремительная сила есть та, с которой тела к некоторой точке, как к центру, отовсюду притягиваются, гонятся или как бы то ни было стремятся".

Таким полем центростремительных сил является пространство вокруг Земли, пространство вокруг магнита, пространство вокруг Солнца. Центростремительная сила в каждой точке такого пространства определяется мощностью самого силового центра, положением точки воздействия и, наконец, массой тела, помещенного в эту точку. В связи с этим Ньютон различает в центростремительной силе три фактора ее: абсолютную, ускорительную и движущую величину.

"Определение VI. Абсолютная величина центростремительной силы есть мера большей или меньшей мощности самого источника ее распространения из центра в окружающее его пространство".

"Определение VII. Ускорительная величина центростремительной силы есть ее мера, пропорциональная той скорости, которую она производит в течение данного времени".

"Определение VIII. Движущая величина центростремительной силы есть ее мера, пропорциональная количеству движения, которое ею производится в течение данного времени".

То, что Ньютон называет "ускорительной силой", есть не что иное, как напряженность силового поля - фундаментальное понятие теории силового поля. Движущая сила пропорциональна как напряженности поля, так и массе тела. Ее можно измерить статическим методом, прилагая к телу силу, препятствующую его перемещению под действием силового поля. Ньютон подчеркивает, что вводимые им понятия являются математическими характеристиками поля. "Эти понятия должно рассматривать как математические,- заявляет он,- ибо я еще не обсуждаю физических причин и места нахождения сил". И несколько ниже он еще раз указывает: "Название же "притяжение" (центром), натиск, или стремление (к центру), я употребляю безразлично одно вместо другого, рассматривая эти силы не физически, а математически, поэтому читатель должен позаботиться, чтобы ввиду таких названий не думать, что я ими хочу определить самый характер действия или физические причины происхождения этих сил или же приписывать центрам (которые суть математические точки) действительно и физические силы, хотя я и буду говорить о силах центров и о притяжении центрами".

Следовательно, Ньютон не склонен объективизировать силу, как это делали ньютонианцы. Он рассматривал ее как математическую категорию, которая позволяет описать то взаимодействие тел, результатом которого являются их ускорения.

Раздел "Определения" заключается знаменитым "Поучением", в котором Ньютон излагает свои взгляды на пространство и время, относительное и абсолютное движение. Ньютон хорошо знает, что наблюдаемые в природе движения имеют относительный характер: "Движение и покой, при обычном их рассмотрении, различаются лишь в отношении одного к другому, ибо не всегда находится в покое то, что таковым простому взгляду представляется",- говорит он в пояснении к "Определению III", и описание их требует задания системы отсчета. Но Ньютон полагал, что можно говорить об абсолютном движении тел, вводя понятие абсолютного пространства и времени. Вот как определяет он эти фундаментальные в его механике понятия:

"I. Абсолютное, истинное математическое время само по себе и по самой своей сущности, без всякого отношения к чему-либо внешнему, протекает равномерно и иначе называется длительностью.

Относительное, кажущееся, или обыденное время есть или точная, или изменчивая, постигаемая чувствами, внешняя, совершаемая при посредстве какого-либо движения, мера продолжительности, употребляемая в обыденной жизни вместо истинного математического времени, как-то: час, день, месяц, год.

II. Абсолютное пространство по самой своей сущности безотносительно к чему бы то ни было внешнему и остается всегда одинаковым и неподвижным.

Относительное есть его мера или какая-либо ограниченная подвижная часть, которая определяется нашими чувствами по положению его относительно некоторых тел и которое в обыденной жизни принимается за пространство неподвижное: так, например, протяжение пространств подземного воздуха или надземного, определяемых по их положению относительно Земли. По виду и величине абсолютное и относительное пространства одинаковы, но численно не всегда остаются одинаковыми. Так, например, если рассматривать Землю подвижною, то пространство нашего воздуха, которое по отношению к Земле остается всегда одним и тем же, будет составлять то одну часть пространства абсолютного, то другую, смотря по тому, куда воздух перешел, и, следовательно, абсолютно сказанное пространство беспрерывно меняется.

III. Место есть часть пространства, занимаемая телом, и по отношению к пространству бывает или абсолютным, или относительным. Я говорю "часть пространства", а не положение тела и не объемлющая его поверхность. Для равнообъемных тел места равны, поверхности же от несходства формы тел могут быть и неравными. Положение, правильно выражаясь, не имеет величины, и оно само по себе не есть место, а принадлежащее месту свойство. Движение целого то же самое, что совокупность движений частей его, т. е. перемещение целого из его места то же самое, что совокупность перемещений его частей из их мест, поэтому место целого то же самое, что совокупность мест его частей, и, следовательно, оно целиком внутри всего тела.

IV. Абсолютное движение есть перемещение тела из одного абсолютного его места в другое, относительное - из относительного в относительное же".

Признавая объективное существование пространства и времени, Ньютон становится на материалистическую точку зрения. Но, отрывая абсолютное пространство и время от реальных вещей и процессов, Ньютон придает этим категориям метафизический характер. Абсолютное время характеризуется, по Ньютону, равномерностью течения; для относительного времени, постигаемого в процессах, например движениях светил, такой равномерности может и не быть. "Возможно, что не существует (в природе) такого равномерного движения, которым время могло бы измеряться с совершенной точностью". Абсолютное пространство Ньютона - это абсолютно неподвижное пространство. "Как неизменен порядок времени, так неизменен и порядок частей пространства. Если бы они переместились из мест своих, то они продвинулись бы (так сказать) в самих себя, ибо время и пространство составляют как бы вместилища самих себя и всего существующего. Во времени все располагается в смысле порядка последовательности, в пространстве - в смысле порядка положения. По самой своей сущности они суть места, приписывать же первичным местам движения нелепо. Вот эти-то места и суть места абсолютные, и только перемещения из этих мест составляют абсолютные движения".

На практике же мы имеем дело с относительными движениями, связывая системы отсчета с теми или иными телами. "Может оказаться, что в действительности не существует покоящегося тела, к которому можно было бы относить места и движения прочих". Абсолютное же время и пространство непостижимы чувствами и теряют свой физический характер, превращаясь в чистые абстракции. Можно было бы обойтись при физических исследованиях и без этих абстракций, оперируя с теми пространственно-временными представлениями, к которым приводит изучение реальных процессов.

Однако Ньютон полагает, что существуют физические способы обнаружения абсолютных движений, т. е. перемещений тел в абсолютном пространстве. Обнаружить равномерное прямолинейное движение системы отсчета невозможно по классическому принципу относительности Галилея, принимаемому и Ньютоном. Но можно обнаружить проявления абсолютного движения системы. Абсолютное движение отличается от относительного тем, что приложенные силы действительно изменяют абсолютное движение тела, в то время как относительное движение может изменяться и без действия сил на тело - достаточно только, чтобы силы действовали на окружающие тела. Если подвесить на веревке сосуд с водой и, закрутив веревку, предоставить ей возможность раскручиваться, то будут наблюдаться следующие явления: сосуд приходит в движение, вода же неподвижна, и ее поверхность плоская. По мере раскручивания веревки вода также начинает вращаться, и это скажется в повышении ее уровня у стенок и понижении в центре - части воды удаляются от оси вращения. Таким образом, в начальный момент относительное движение сосуда и воды было наибольшим, однако никаких проявлений этого относительного движения воды не наблюдалось. Затем относительное движение сосуда и воды уменьшилось, вода пришла во вращение так же, как и сосуд, и это проявилось в удалении частиц воды от оси вращения. Вот это-то стремление вращающихся тел удалиться от оси вращения и дает возможность распознать абсолютное вращение. "Таким способом,- говорит Ньютон,- могло бы быть определено количество и направление кругового движения внутри огромного пустого пространства, где не существовало бы никаких внешних доступных чувствам признаков, к которым можно было бы относить положения шаров^*. Если бы в этом пространстве, кроме того, находились еще некоторые весьма удаленные тела, сохраняющие относительное друг к другу положение, подобно тому, как наши неподвижные звезды, то по перемещению шаров относительно этих тел мы не могли бы определить, чему принадлежит это перемещение - телам или шарам. Но если бы мы, определив натяжение нити, нашли, что это натяжение как раз соответствует движению шаров, то мы заключили бы, что движение принадлежит шарам, а не внешним телам и что эти тела находятся в покое".

^* (Речь идет у Ньютона о воображаемом опыте исследования вращательного движения шаров, связанных нитью, ось вращения которых проходит через центр тяжести шаров. По натяжению нити можно констатировать, вращаются шары или нет.)

Ньютон и полагает, что задачей механики является "нахождение... истинных движений по причинам, их производящим, по их проявлениям и по разностям кажущихся движений и, наоборот, нахождение по истинным или кажущимся движениями их причин и проявлений". Так вошла в физику ньютонианская концепция абсолютного пространства и времени.

Установив систему отсчета, покоящуюся в абсолютном пространстве, Ньютон переходит к формулировке законов механики в этой системе. Эти знаменитые законы Ньютона формулируются им следующим образом.

"Закон I. Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние".

"Закон II. Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует".

"Закон III. Действию всегда есть равное и противоположное противодействие, иначе - взаимодействия двух тел друг на друга равны и направлены в противоположные стороны".

Стержнем ньютоновской динамики является второй закон, который математически можно записать так:

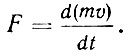
Сила, как указывает третий закон, всегда является взаимодействием между телами. Она определяется конфигурацией взаимодействующих тел, т. е. их массами и взаимными расстояниями. Она не будет зависеть от состояния тела и от наличия других сил. Отсюда вытекает в качестве следствия принцип суперпозиции сил, формулируемый Ньютоном в виде правила параллелограмма сил. Это следствие дает возможность Ньютону перекинуть мост от динамики к статике; он трактует действие простых машин, разлагая и складывая действующие силы по правилу параллелограмма. Таким путем он выводит закон равновесия косого рычага и действие наклонной плоскости. А это дает возможность вывести "соотношения между усилиями в машинах, составленных из колес, барабанов, воротов, рычагов, блоков, натянутых канатов и других механизмов, и весами грузов, поднимаемых или прямо, или наклонно, а также силы связок, приводящих в движение кости животных".

Из третьего и второго законов Ньютон выводит закон сохранения количества движения для замкнутой системы, т. е. системы, не подверженной действиям внешних сил, а только взаимодействиям тел, входящих, в эту систему (следствие III). В следствии IV утверждается: "Центр тяжести системы двух или нескольких тел от взаимодействия тел друг на друга не изменяет ни своего состояния покоя, ни движения, поэтому центр тяжести системы всех действующих друг на друга тел (при отсутствии внешних действий и препятствий) или находится в покое, или движется равномерно и прямолинейно".

"Следовательно,- заключает Ньютон,- по отношению к центру тяжести системы нескольких тел имеет место тот же самый закон сохранения состояния покоя или равномерного и прямолинейного движения, как и для одного тела. Таким образом, поступательное количество движения отдельного ли тела, или системы тел надо всегда рассчитывать по движению центра тяжести их". Так Ньютон устанавливает это весьма важное для динамики системы предложение.

Наконец, из принципа независимости действия сил и из того, что силы взаимодействия определяются только расстоянием между телами, вытекает классический принцип относительности Галилея - Ньютона.

"Следствие V. Относительные движения друг по отношению к другу тел, заключенных в каком-либо пространстве, одинаковы, покоится ли это пространство или движется равномерно и прямолинейно без вращения".

Точно так же относительное движение тел не изменяется, если приложить одновременно ко всем телам равные и одинаково направленные силы.

Раздел "Начал", посвященный изложению аксиом движения и ближайших следствий из них, заключается "Поучением", в котором идет речь об опытной проверке законов движения. Первые два закона и вытекающий из них принцип независимости действия сил подтверждены опытами Галилея над падающими телами. Отправляясь от тех же законов, можно вывести формулу качания маятника, которая подтверждена уже практикой с часами. Третий закон динамики был подтвержден опытами Рена и Мариотта над ударами шаров. Сам Ньютон повторил эти опыты с большей точностью, введя поправку на сопротивление воздуха. Он нашел, что "третий закон по отношению к удару и отражению подтверждается теорией, вполне согласующейся с опытом".

Подтверждается третий закон и для взаимодействий на расстоянии. Если бы эти взаимодействия не были равны, то, поместив между взаимно притягивающимися телами препятствие, мешающее их сближению, можно было бы обнаружить, как это препятствие уступает действию большей силы. "Я производил подобный опыт с магнитом и железом; если их поместить каждый в отдельный сосуд и пустить плавать на спокойной воде так, чтобы сосуды взаимно касались, то ни тот, ни другой не приходит в движение, но вследствие равенства взаимного притяжения сосуды испытывают равные давления и остаются в равновесии". Точно так же, если бы взаимные притяжения частей Земли не уравновешивались, то Земля ушла бы ускоренным движением в бесконечность.

Ньютон считал особенно необходимым подтвердить экспериментально третий закон, как новый и впервые в отчетливой форме высказанный им. Этим объясняется и то, что сам он проделал опыты, подтверждающие этот закон, и то, что он указывает далее на большой опытный материал, доставляемый статическими машинами. "Подобно тому, как при ударе и отражении тела, коих скорости обратно пропорциональны массам, равнозначащи, так и при движении механических приборов действующие силы, коих скорости, взятые по направлению самих сил (проекции скорости точки приложения каждой силы на направление этой силы), обратно пропорциональны этим силам, равнозначащи между собой, и при стремлении в противоположные стороны взаимно уравновешиваются. Так обстоит дело в рычаге, блоке, наклонной плоскости, винте, часах и во всякого рода машинах... Действительность и назначение машин в том только и состоит, чтобы, уменьшая скорость, увеличивать силу, и наоборот, ибо во всех подобного рода приборах в сущности решается такая задача: заданный груз двигать заданною силой или же заданное сопротивление преодолеть заданным усилием". И Ньютон заключает поучение многозначащим выводом:

"Дальнейшее изложение учения о машинах сюда не относится, я хотел лишь показать, сколь далеко простирается и сколь благонадежен третий закон движения. Если действие движущей силы оценивать пропорционально произведению этой силы и скорости и подобно этому противодействие сопротивлений оценивать для каждой части в отдельности пропорционально произведению ее скорости и встречаемого ею сопротивления, происходящего от трений, сцепления, веса и ускорения, то во всякой машине действие и противодействие будут постоянно равны, и поскольку действие передается машиной и в конце прилагается к сопротивляющемуся телу, то это последнее его значение будет обратно значению противодействия".

"В этих заключительных словах поучения,- комментирует академик Крылов,- можно видеть не только начало возможных перемещений в его всеобъемлющем приложении к учению о равновесии машин, т. е. вообще систем тел с полной связью или одною степенью свободы, но и сущность принципа Д'Аламбера, лишь высказанную в столь сжатой форме, что нужен был гений Лагранжа, чтобы это общее начало выразить одною математическою формулой, включающей в себя всю статику и динамику".

Так Ньютон привлекал для обоснования механики весь современный ему механический опыт. Законы Ньютона подтвердились дальнейшим развитием механики с исключительной точностью. Только в области больших скоростей, с одной стороны, и для весьма малых частиц, с другой, выявились отступления от ньютоновских законов. В земной и небесной механике ньютоновы законы сохраняют полностью свою силу. Ближайшая задача состояла в том, чтобы развить со всей полнотой следствия из этих законов. Этой задаче и посвящено содержание "Начал".