Тяготение

Основная тема "Начал" - это изучение движений тел под действием центральных сил и в особенности динамическое обоснование системы Коперника. Это обоснование было найдено Ньютоном в его знаменитом законе всемирного тяготения. Рассмотрим коротко историю открытия этого закона.

Как мы знаем, Аристотель считал тяжесть естественным стремлением тел к центру мира, который он полагал в центре Земли. Коперник должен был отвергнуть эту точку зрения, как противоречащую его системе. Он отчетливо высказывает мысль, что тяжесть присуща всем небесным телам. "По моему мнению,- пишет Коперник,- тяжесть есть не что иное, как естественное устремление, которым божественное провидение творца миров одарило части для сочетания и соединения их в единое целое в форме сферы. Такое стремление свойственно, вероятно, Солнцу, Луне и прочим блуждающим светилам, и благодаря его действию они сохраняют свою очевидную шарообразность, несмотря на многообразие совершаемых ими обращений"^*.

^* (Николай Коперник, Изд. АН СССР, 1947, стр. 208.)

К этой точке зрения присоединяется Галилей в своем "Диалоге".

Более полно ее развивает Кеплер, уподобляя силу тяжести магнитному притяжению: "Тяжесть есть взаимная склонность между родственными телами, стремящимися слиться, соединиться воедино; магнитная способность есть свойство того же порядка; скорее Земля притягивает камень, чем камень стремится к Земле... Если бы в каком-нибудь месте мира находились два камня на близком расстоянии друг от друга и вне сферы действия какого бы то ни было родственного им тела, то эти камни стремились бы соединиться друг с другом, подобно двум магнитам, где-нибудь посредине этого расстояния, и пути, которые им пришлось бы пройти, были бы обратно пропорциональны их массам"^*.

^* (Цитировано по Дюгему, Физическая теория, 1910, стр. 277.)

Эта точка зрения оживленно обсуждалась в работах ученых XVII в. Учение Аристотеля было оставлено, но новый взгляд вырабатывался с трудом. Метафизическим спорам противостояли реальные факты: спутники Юпитера, законы Кеплера,- и надо было решить вопрос, какие же силы удерживают спутников вокруг планет, а сами эти планеты - около Солнца. Закон тяготения был скрыт в этих фактах, он содержался в законах Кеплера, и сам Кеплер предчувствует это. Во вступлении к своей "Новой астрономии", содержащей два его первых закона, мы читаем: "Всякая телесная субстанция способна оставаться в покое во всяком месте, если она находится здесь одна и устранена от сферы влияния всякого другого тела... Естественное движение - не круговое, как утверждали древние, а прямолинейное... Если сила Луны простирается до Земли, то тем по большей причине сила Земли простирается до Луны и даже дальше. Ничто из того, что аналогично по свойствам с Землею, не может избежать этой влекущей силы..."^*.

^* (Цитировано по книге: Е. А. Предтеченский, Иоганн Кеплер, Спб, 1891, стр. 53.)

Разбирая вопрос о причине движения планет вокруг Солнца, Кеплер решает его в том смысле, что в Солнце есть сила, увлекающая планеты, действующая в плоскости планетных орбит. "Я утверждаю, что тело Солнца - магнитно; что Солнце вращается вокруг себя в ту же сторону, как и планеты, но вращение это гораздо быстрее, чем обращение всякой планеты"^*.

^* (Цитировано по книге: Е. А. Предтеченский, Иоганн Кеплер, Спб, 1891, стр. 56.)

В 1619 г. Кеплер выпустил "Мировую гармонию", содержащую третий закон: "Отношение между периодами обращения любых планет в точности равно полуторному отношению их средних расстояний или радиусов орбит". Здесь он описывает причины, влекущие планеты вокруг Солнца, в следующих выражениях: "... или движущие их (планеты.- П. К.) духи становятся слабее по мере удаления своего от Солнца, или что существует один движущий дух, заключенный в центре всех орбит, именно в Солнце, и действующий на планету сильнее, когда он находится от нее ближе, и слабее - на более далеких расстояниях, вследствие этой отдаленности"^*.

^* (Цитировано по книге: Е. А. Предтеченский, Иоганн Кеплер, Спб, 1891, стр. 77.)

Слово "дух" (spiritus) в те времена понималось как некоторое тонкое истечение и было весьма употребительно в естественнонаучных сочинениях. Мы встречаем этот термин и у Бэкона, и у Ньютона, и у их современников. Он нередко отождествлялся с эфиром. Во всяком случае найти материальную причину тяготения, действующего на громадные расстояния без посредства видимой осязаемой материи, было нелегко; и термин "сила", заменивший кеплеровский "дух", был ничуть не более "вещественным". Декарт пытался наметить более наглядную картину тяготения в виде вихревых движений опять-таки неощущаемой материи. Эта концепция имела тот недостаток, что не давала возможности количественного объяснения и, в частности, как справедливо указывал Коте в предисловии к ньютоновским "Началам", не согласовалась с законами Кеплера. Накопление динамических знаний давало возможность все более и более точно описывать процесс движения планет. В 1666 г. флорентийский академик Борелли уже почти правильно рисует механику движения планет: "Предположим, что планета стремится к Солнцу и в то же время своим круговым движением удаляется от этого центрального тела, лежащего в середине круга. Если обе эти противоположные силы равны между собой, то они должны уравновеситься - планета не будет в состоянии ни приблизиться к Солнцу, ни отойти от него дальше известных пределов - и в таком равновесии будет продолжать свое обращение около Солнца".

В 1673 г. Гюйгенс своей теорией центробежных сил дал динамику кругового движения. В 1674 г. английский ученый Роберт Гук (1635-1703) дает общую динамическую картину солнечной системы, основанную на трех идеях:

1. существовании взаимного тяготения всех небесных тел;
2. "все тела, раз приведенные в прямолинейное и простое движение, будут двигаться по прямой линии, если не будет какой-либо другой действующей силы, отклоняющей их и принуждающей двигаться по кругу, эллипсу или другим более сложным кривым линиям";
3. эти силы увеличиваются с уменьшением расстояния.

Однако закона зависимости силы тяготения от расстояния Гук не нашел. Открытие закона составило заслугу Ньютона.

Первое печатное упоминание о размышлениях Ньютона над проблемой тяготения мы находим в его оптическом мемуаре 1675 г. "Одна гипотеза, объясняющая свойства света". Речь идет о гипотезе эфирных истечений "духов". Ньютон, указывая, что электрическая пляска бумажек под стеклом может быть объяснена движениями некоторой тонкой материи, пишет:

"Гравитационное притяжение Земли может также причиняться непрерывной конденсацией некоторого иного, схожего эфирного газа".

"Если это так,- продолжает Ньютон,- то обширное тело Земли, каковое всюду может быть действительным центром вечной работы, способно непрерывно сгущать такое количество этого газа, чтобы вызывать нисхождение его сверху с большой скоростью для использования. При таком нисхождении этот газ может увлекать с собою тела, через которые он проходит, с силою пропорцональной поверхностям всех частиц тел, на которые действует"^*.

^* (И. Ньютон. Одна гипотеза, объясняющая свойства света, перевод С. И. Вавилова, Успехи физических наук, Гостехиздат, 1927, т. VII, вып. 2, стр. 138. Вавилов переводит здесь слово spiritus - "дух" - словом "газ".)

Это место напоминает высказывания Кеплера о "духе", исходящем из Солнца и увлекающем планеты. Однако у Кеплера эти гравитационные истечения действовали в определенной плоскости, у Ньютона они действуют в пространстве, сила этих истечений определяется площадью действия и, таким образом, убывает обратно пропорционально квадрату расстояния, наподобие освещенности от данного источника света. Эта оптическая аналогия соответствует другой оптической аналогии: прямолинейность светового луча в однородной среде соответствует прямолинейному равномерному инерционному движению. В свою очередь, прямолинейность луча определила геометрию пространства, в котором распространяются свет и тяготение,- это эвклидово пространство. Абсолютное пространство Ньютона подчиняется законам эвклидовой геометрии; прямолинейность инерционного движения и закон обратной пропорциональности квадратов для гравитационного притяжения точкой теснейшим образом связаны с геометрическими свойствами ньютоновского пространства.

Известная легенда (имеющая, по-видимому, некоторые основания) о яблоке, упавшем в саду и заставившем Ньютона задуматься над вопросом о расстоянии, на котором действует сила тяжести, свидетельствует, что ко времени написания мемуара закон квадратов был уже выношен Ньютоном. Он распространил этот закон на движение Луны. Результаты его исследований в окончательном виде сформулированы в "Началах" в виде следующего предложения: "Луна тяготеет к Земле и силою тяготения постоянно отклоняется от прямолинейного движения и удерживается на своей орбите". Ньютон доказывает это предложение следующим расчетом. Примем среднее расстояние Луны от Земли равным 60 радиусам Земли. Время одного оборота Луны вокруг Земли 27 суток 7 часов 43 мин. Окружность Земли по измерениям, предпринятым во времена Ньютона, 123 249 600 парижских фута. Если из этих данных вычислить центростремительное ускорение Луны, то оказывается, что Луна падает на Землю ускоренно так, что при отсутствии начальной скорости она прошла бы за первую минуту путь в 15 ¹/₁₂ парижского фута. "Так как,- пишет Ньютон,- при приближении к Земле сила эта возрастает в обратном отношении квадратов расстояний, то у поверхности Земли она будет в 60*60 раз более, нежели на орбите Луны; тело, падающее под действием такой силы в наших местах, стало бы описывать в первую минуту 60*60*15 ¹/₁₂ пар. фут., в первую же секунду 15 ¹/₁₂, или, точнее, 15 фут 1 дюйм 1 ⁴/₉ линий. Действительно, тяжелые тела и падают на Землю под влиянием такой силы, ибо длина маятника, делающего на широте Парижа свои размахи в одну секунду, равна 3 футам 8 ¹/₂ линии пар., как это наблюдал Гюйгенс. Отношение же высоты, проходимой телом при падении в первую секунду, к длине такого маятника равно квадрату отношения окружности к диаметру (как показано также Гюйгенсом), следовательно, эта высота равна 15 фут. 1 дюйму 1 ⁷/₉ линии пар. Итак, сила, которою Луна удерживается на своей орбите, если ее опустить до поверхности Земли, становится равной силе тяжести у нас, поэтому ... она и есть та самая сила, которую мы называем тяжестью, или тяготением"^*.

^* (И. Ньютон, Математические начала натуральной философии, "Известия Николаевской Морской академии", вып. V, 1916, стр. 458-459.)

Этот расчет сыграл важную роль в утверждении закона тяготения. Но отсюда видно, как сильно зависит научный прогресс от коллективной работы ученых. Для того чтобы открыть закон тяготения, недостаточно было единичных усилий даже такого гения, как Ньютон. Он опирался на точные многовековые наблюдения движения Луны и астрономические определения ее расстояния от центра Земли, на градусные измерения, проведенные Пикаром в Париже в 1675 г., и, наконец, на замечательные исследования Гюйгенса.

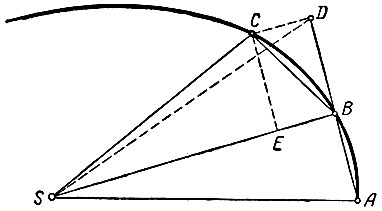
Рис. 3-7. К выводу закона тяготения

Но особенно важную роль в открытии закона тяготения сыграли законы Кеплера. Из этих законов чисто математически (это и было сделано Ньютоном в "Началах") вытекает, что на планеты действует сила, направленная к Солнцу, обратно пропорциональная квадрату расстояния от Солнца. Элементарный расчет второго утверждения на основе III закона Кеплера приводится в школьных учебниках. Менее известен элементарный вывод первого утверждения из второго закона. Приведем здесь этот вывод (рис. 3-7). Пусть планета из некоторого положения А, когда она находилась от Солнца на расстоянии SA в течение такого малого промежутка времени Δt, что ее путь за это время можно считать прямолинейным, перешла в положение Б. В следующий такой же промежуток времени она пройдет отрезок ВС, причем по второму закону Кеплера площадь треугольника ASB равна площади треугольника BSC. Если бы в точке В не действовала сила притяжения, то за второй промежуток времени планета переместилась бы в направлении А В на расстояние BD = AB. Нетрудно доказать равенство площадей треугольников ASB и BSD, а следовательно, и равенство площадей BSD и BSC. Но эти треугольники имеют общее основание BS, а следовательно, и общую высоту, это означает, что фигура CDBE является параллелограммом и геометрическое приращение скорости, пропорциональное отрезку CD, направлено по BE, т. е. к Солнцу.

Ньютон, установив, что Кеплеровы законы определяются силой тяготения планеты к Солнцу, что Луна тяготеет к Земле, спутники Юпитера - к Юпитеру, приходит к следующему важному выводу:

"Все тела тяготеют к каждой отдельной планете и веса тел на всякой планете при одинаковых расстояниях от ее центра пропорциональны массам этих планет".

Это важное предложение в современной науке называется законом пропорциональности инертной и гравитационной масс.

В законах Ньютона были указаны два способа сравнения масс: по весу и по ускорению, получаемому ими от одинаковых сил. Независимость ускорения тяжести от массы указывала на совпадение этих мер. Сформулированное выше предложение Ньютон доказывал опытом с маятниками, к которым в качестве грузов подвешивались кадочки, заполненные деревом, золотом, свинцом, стеклом, песком, солью, водой, пшеницей. Оказывалось, что при одинаковой длине маятников они качались одинаково, независимо от характера вещества, составляющего груз маятника. Распространяя результаты этого опыта на все планеты, Ньютон в конце концов приходит к знаменитому обобщению:

"Тяготение существует ко всем телам вообще и пропорционально массе каждого из них"^*.

^* (И. Ньютон, Математические начала натуральной философии, "Известия Николаевской Морской академии", вып. V, 1916, стр. 464.)

Так был открыт закон всемирного тяготения. Ньютон не исключал возможности объяснения тяготения с помощью определенных физических агентов, в частности с помощью тех же эфирных истечений, о которых он думал вначале. Но он считал, что для такого объяснения нет достаточных данных, "гипотез же я не измышляю", добавлял он. Реакционные последователи Ньютона (их стали называть ньютонианцами), опираясь на это изречение Ньютона, стали требовать изгнания из физики всяких гипотез, ограничивая задачу физики формальным описанием явлений. Передовые деятели науки справедливо усматривали в этом опасность для развития науки и на протяжении всей истории физики боролись со сторонниками "чистого описания".