Гидростатика и аэростатика

Существенные результаты были получены и в механике сплошных сред. Трактаты Стевина, Галилея и Паскаля заложили основы гидростатики, восстановив в правах Архимеда и дав новое обоснование его знаменитому закону. Стевин в своих "Принципах равновесия" (1586 г.) доказывает закон Архимеда, опираясь на принцип отвердевания. Представим себе жидкость в сосуде, находящуюся в равновесии. Очевидно, что равновесие не будет нарушено, если часть жидких частиц утратит свою подвижность и некоторый объем внутри жидкости приобретет свойства твердого тела. Так как этот объем находится в равновесии, то очевидно, что вес его уравновешивается равнодействующей сил давлений со стороны, окружающей выделенный объем жидкости. Таким образом, на тело, погруженное в жидкость, действует сила, направленная вертикально снизу вверх и равная весу жидкости в объеме тела.

В том же сочинении Стевин доказывает экспериментально и теоретически парадокс - независимость весового давления от формы сосуда - и вычисляет давление на боковую стенку. Все эти расчеты нужны ему для выяснения условий плавания тел, в первую очередь кораблей. Стевин писал свои работы на голландском языке, поэтому вполне понятно, что они остались неизвестными Галилею и Паскалю. Галилей в своем "Рассуждении о телах, пребывающих в воде", опровергая мнение перипатетиков о зависимости плавания от формы тел, восстанавливает закон Архимеда. Возражение перипатетиков, что всякая плоская пластина должна плавать, Галилей опровергает опытом, согласно которому плоская пластина большего удельного веса, чем вода, не всплывает. В погружении или плавании тел играет роль плотность. Так, восковой шарик тонет в воде, но если к ней подбавить соли, то при надлежащей концентрации он всплывает. Интересно отметить, что, признавая факт плавания плоских тяжелых пластин, Галилей указал, что такие пластины плавают в углублении поверхностной пленки. Галилею известен факт образования капель воды на капустных листьях и растекания их при смачивании листа красным вином. От испытующего взора великого ученого не ускользнули, таким образом, и явления, связанные с поверхностным натяжением жидкостей. Его ученики в Флорентийской академии (в особенности Борелли) вплотную приступили к изучению явлений капиллярности. Но время для объяснения этих явлений еще не настало.

Блэз Паскаль (1623-1662) в своем трактате о равновесии жидкостей разбирает вопрос наиболее исчерпывающим образом: закон всесторонней передачи давления в жидкости (закон Паскаля), вычисление весового давления и гидростатический парадокс, закон сообщающихся сосудов и принцип гидростатического пресса - все это он выводит, широко применяя принцип возможных перемещений. Классические исследования Паскаля о равновесии жидкостей перешли почти без изменения в школьные учебники вместе с его результатами в изучении атмосферного давления, о которых было сказано выше.

Блэз Паскаль

Открытие давления воздуха имело огромное значение. Особенно важен факт открытия способа изменять упругость газов по определенному закону. Открытие это произошло при следующих обстоятельствах.

Люттихский профессор иезуит Линус высказал мысль, что никакого давления атмосферы не существует, а столб ртути в барометре удерживается особыми невидимыми нитями. Возражая Линусу, знаменитый английский химик Роберт Бойль (1627-1691) решил показать, как можно упругостью воздуха уравновесить вес столба ртути, и, взяв изогнутую трубку с запаянным коротким концом, подливал в открытый конец длинного колена ртуть. Чем меньше становился объем воздуха в закрытом колене, тем большей длины столб ртути уравновешивал его упругость. Помощник Бойля Ричард Тоунли заметил из таблиц Бойля, что упругость воздуха изменялась обратно пропорционально его объему. Бойль признал справедливость этого вывода и доказал его для давлений ниже атмосферного. Описание опытов Бойля и формулировка его закона содержится в его сочинении "Защита доктрины, касающейся упругости веса воздуха" (1662 г.). В 1676 г. французский священник Эдм Мариотт (1620-1684) в сочинении "Опыты о природе воздуха" описывает многочисленные опыты по сжатию и разрежению воздуха, из которых он выводит основной закон независимо от Бойля. Здесь же он дает приближенную барометрическую формулу.

Теоретический анализ законов гидростатики и аэростатики был дан Ньютоном. В "Началах" Ньютон определяет жидкость как тело, "коего части уступают всякой как бы то ни было приложенной силе и, уступая, свободно движутся друг относительно друга". Это определение Ньютона охватывает как собственно жидкости, так и газы. В дальнейшем Ньютон рассматривает как несжимаемую, так и сжимаемую жидкости, принимая для последней, что плотность ее пропорциональна давлению, т. е. жидкость подчиняется закону Бойля-Мариотта. Ньютон доказывает, что если такая сжимаемая жидкость будет находиться в поле центральных сил, то плотность ее будет изменяться с расстоянием от центра по закону, зависящему от закона силы. В частности, в однородном поле тяжести плотность, а следовательно, и давление меняются с высотой по барометрической формуле, "как это нашел знаменитейший Эдмунд Галлей",- прибавляет Ньютон. Галлей дал вывод барометрической формулы в 1686 г. В заключении пятого отдела второй книги "Начал", в котором излагаются эти теоремы, Ньютон показывает, что закон Бойля-Мариотта может быть выведен математически, если предположить, что жидкость состоит из частиц, взаимно отталкивающихся с силами, обратно пропорциональными расстоянию между их центрами. "Состоит ли жидкость на самом деле из взаимно отталкивающихся частиц, есть вопрос физический",- пишет Ньютон. "Мы доказали математически свойства жидкостей, состоящих из таких частиц, и предоставляем физикам повод исследовать этот вопрос". Физически обоснованный вывод закона Бойля-Мариотта был дан Д. Бернулли и М. В. Ломоносовым позднее, на основе атомно-кинетических представлений.

Роберт Бойль

Ньютон рассматривает и вопросы кинематики и динамики жидкостей. До него первый существенный результат был получен Торричелли, который в 1646 г. нашел известную формулу для скорости истечения жидкости из отверстия. Гидродинамика Ньютона особенно замечательна в том отношении, что он впервые в науке начал теоретически исследовать движение тела в вязкой жидкости. Седьмой отдел второй книги его "Начал" открывается знаменитой теоремой о подобии. Эта теорема определяет условия, при которых две подобные механические системы совершают подобные движения, т. е. движение второй системы во всем (кроме масштаба) копирует движение первой системы. Ньютон называет системы подобными, если они состоят из одинакового числа частиц, расположенных подобным образом.

Сформулировав условия динамического подобия, Ньютон вывел из них закон для силы сопротивления тела, движущегося в вязкой жидкости. Этот закон выражается формулой:

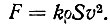
Весьма важен восьмой отдел второй книги "Начал", в котором Ньютон рассматривает передачу движения жидкостью. Здесь Ньютон рассматривает закон распространения волн в упругой среде. Он показывает, что волны при встрече с препятствием уклоняются (дифрагируют) от прямолинейного распространения, и находит, что скорость распространения волн в упругих жидкостях прямо пропорциональна корням квадратным из их упругости и обратно пропорциональна корням квадратным из плотностей, причем предполагается Бойлева зависимость между упругостью и плотностью газа.

Формула Ньютона 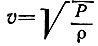не согласуется с опытом, так как упругость меняется со сжатием не по закону Бойля-Мариотта, а по адиабатическому закону (уравнению Пуассона). Она была исправлена Лапласом. Сам Ньютон объяснял расхождение вычисленной по его формуле величины скорости звука с результатами опытных измерений тем, что в воздухе имеются твердые частицы и водяные пары, изменяющие величину его упругости.

Замечательно, что свою теорию распространения волн Ньютон считал неприложимой к свету. "Так как свет распространяется по прямым линиям, то он не может состоять из одного только давления", т. е. не передается через упругую среду, подобно давлению. Звук же распространяется волнами. Поэтому Ньютон, хотя и считал свет механическим процессом, отличал распространение света от распространения звука. Его современник Гюйгенс, напротив, усматривал полную аналогию в распространении звука и света. Осветим теперь более подробно вопрос о состоянии оптики в XVII в.