Механика

Наиболее продвинулась в период завершения научной революции механика. Уточнились ее основные понятия, были введены новые важные понятия, развились ее принципы и методы. Рассмотрим кратко основные моменты развития механики после Ньютона.

Готфрид Вильгельм Лейбниц

В ньютоновской механике сила измеряется изменением количества движения за единицу времени, причем количество движения определяется произведением массы тела на его скорость (mv). Эта мера движения была известна в XVII в. как мера Декарта. Лейбниц (1646-1716) в 1686 г. выступил с критикой этой меры, утверждая, что в природе сохраняется величина mv2, которой и определяется мера "живой силы". Этим утверждением Лейбница в науку было введено понятие кинетической энергии, которое долгое время (еще ив XX веке) встречалось также под названием "живой силы". Вместе с тем выступление Лейбница положило начало ожесточенному спору о двух мерах движения. Д'Аламбер (1717-1783) в своей "Динамике" (1743 г.) указал, что с одинаковым успехом можно применять и ту и другую меру. Если измерять "силу" движущегося тела величиной препятствий, преодолеваемых им, т. е., говоря современным языком, работой, совершаемой телом за счет энергии движения, то надо применять меру Лейбница, если же ее измерять "суммой сопротивлений препятствию", т. е. величиной импульса сил ∑F*Δt, то справедлива мера Декарта. В дальнейшем Энгельс в "Диалектике природы" раскрыл философское значение этого спора о мерах движения. Следует отметить, что принцип "живых сил", которым уже пользовались Галилей и Гюйгенс в XVII в., с успехом использовался при решении ряда задач механики. Так, Иоганн Вернулли (1667-1748) применил его для решения задачи об упругом ударе, задачи о физическом маятнике, о колебаниях струны. Его племянник Даниил Бернулли (1700-1782) (бывший одно время членом Петербургской Академии наук) показал, что для случая системы точек, взаимодействующих с центральными силами, изменение "живой силы" системы определится только начальной и конечной конфигурацией системы. Д. Бернулли применил закон "живых сил" к рассмотрению движения идеальной жидкости и получил известное в гидродинамике уравнение Бернулли.

Жан Лерон Д'Аламбер

Наконец, Лагранж (1736-1813) в своей "Аналитической механике" (1788 г.) дал общий вывод уравнения "живых сил" как первого интеграла дифференциальных уравнений механики.

Спор о мерах движения был тесно связан с вопросом об источниках движения. В этом важном вопросе особенно давало себя знать "крепостничество в идеях", т. е. остатки старого, средневекового, церковного мировоззрения. Ньютон не мог решить этого вопроса и предоставил "первый толчок" богу. Более того, поскольку механическое движение в природе постепенно рассеивается, бог, по мнению Ньютона, должен время от времени пополнять запас движения во Вселенной. Против этой концепции выступали передовые ученые, отстаивавшие принцип сохранения движения. К числу этих ученых принадлежали И. Бернулли, Л. Эйлер и особенно М. В. Ломоносов.

Жозеф Луи Лагранж

Ломоносов считал совершенно необходимым при решении любого физического или химического вопроса опираться на закон сохранения материи и движения. По мнению материи и движения, по мнению Ломоносова, любые изменения в природе обязательно связаны с сохранением некоторого инварианта. В 1748 г. он писал в письме Эйлеру: "Но все встречающиеся в природе изменения происходят так, что если к чему-либо нечто прибавилось, то это отнимается от чего-то другого. Так, сколько материи прибавляется к какому-либо телу, столько же теряется у другого, сколько часов я затрачиваю на сон, столько же отнимаю от бодрствования, и т. д. Так как это всеобщий закон природы, то он распространяется и на правила движения: тело, которое своим толчком возбуждает другое к движению, столько же теряет от своего движения, сколько сообщает другому, им двинутому".

На глубину и общность этой формулировки Ломоносова впервые указал в 1949 г. С. И. Вавилов. Ломоносов не определяет ближе природы инварианта ("нечто"), справедливо полагая, что она раскрывается в конкретных изменениях и превращениях; только в качестве примеров он приводит сохранение материи, временного интервала, движения. Весьма замечательно утверждение Ломоносова о сохранении временного интервала, его однородности, "нерастяжимости". Современная физика вообще считает законы сохранения непосредственным следствием свойств однородности пространства и времени Вполне прав был С. И. Вавилов, когда писал о формулировке Ломоносова: "Это начало есть закон всеобщей, объемлющий всю объективную реальность с пространством, временем, веществом и прочими ее свойствами и проявлениями". Такое глубокое понимание значения основных законов науки, законов сохранения давало возможность Ломоносову бороться с метафизическими концепциями "флюидов" и "дальнодействующих сил", господствующими в физике XVIII в.

Концепция дальнодействующих сил критиковалась также Эйлером и Д'Аламбером. Эйлер принимает в качестве общих свойств материи ее протяженность, подвижность, инерцию, непроницаемость. По мнению Эйлера, инерция в соединении с непроницаемостью тел образует "богатейший источник сил, способных непрерывно изменять состояние тел". Сила у Эйлера - это взаимодействие тел, обусловленное их инерцией и непроницаемостью. Вместе с Декартом Эйлер считает, что всякое взаимодействие является контактным, т. е. принимает, что действие на расстоянии, вроде тяготения или магнитных и электрических взаимодействий, является результатом движений скрытой материи - эфира. Аналогичную концепцию развивает и Ломоносов. Д'Аламбер вообще не считает нужным вводить в механику силы, "как понятия неясные и метафизические, способные лишь распространить мрак над ясной самой по себе наукой". Для построения динамики, по Д'Аламберу, достаточно трех принципов: принципа инерции, принципа суперпозиции движений, принципа равновесия. Этот последний принцип вошел в науку под названием "принципа Д'Аламбера". Суть его заключается, как известно, в том, что движение точки (а также системы точек) можно рассматривать как состояние подвижного равновесия трех сил: приложенной к данной точке внешней силы, силы реакции связи (в случае наличия таковой) и "силы инерции", равной произведению массы точки на ее ускорение, взятое с обратным знаком. Сам Д'Аламбер формулирует этот принцип, не прибегая к термину "сила", а употребляя вместо него "движение".

Принцип Д'Аламбера позволяет свести динамическую задачу к статической. Статика к этому времени обогатилась важной "теоремой Вариньона" и принципом возможных скоростей Иоганна Бернулли Оба эти результата содержались в сочинении Вариньона (1664-1722) "Новая механика", вышедшем в 1725 г. Теорема Вариньона заключается в следующем. Если имеются две силы, действующие под углом друг к другу на одну и ту же точку, то их равнодействующая по величине и направлению выражается диагональю параллелограмма, образованного из отрезков, представляющих данные силы. Если, далее, в плоскости этого параллелограмма взять точку и опустить из нее перпендикуляры на направления сил, то произведение силы на длину перпендикуляра будет моментом силы относительно взятой точки. Теорема Вариньона утверждает, что алгебраическая сумма моментов составляющих сил равна моменту равнодействующей. При этом знак момента определяется направлением, в котором данная сила стремится вращать в плоскости выбранную точку.

Принцип возможных скоростей был приложен к сочинению Вариньона в виде письма Бернулли (1717 г.). Фактически этот принцип уже применялся Гвидо Убальди в его теории рычага, Галилеем в его теории наклонной плоскости, Торричелли, указавшем, что два связанных груза находятся в равновесии, когда центр тяжести их занимает наинизшее положение. Принцип Бернулли Лагранж в своей "Аналитической механике" (1788 г.) формулирует следующим образом: "Если какая-либо система любого числа тел или точек, на каждую из которых действуют любые силы, находится в равновесии и если этой системе сообщить любое малое движение, в результате которого каждая точка пройдет бесконечно малый путь, представляющий ее виртуальную скорость, то сумма сил, помноженных каждая соответственно на путь, проходимый по направлению силы точкой, к которой она приложена, будет всегда равна нулю, если малые пути, проходимые в направлении сил, считать положительными, а проходимые в противоположном направлении считать отрицательными". При этом под виртуальной скоростью Лагранж понимает ту скорость, которую получило бы тело, если бы начало двигаться при нарушении равновесия, т. е. его понимание отлично от современного, когда под виртуальным перемещением мы понимаем любое возможное перемещение, совместимое со связями.

Принцип Бернулли дал повод Мопертюи в 1774 г. выступить с формулировкой принципа наименьшего действия. Математическая формулировка принципа Мопертюи была дана Эйлером. Этот принцип сыграл важную роль в истории теоретической физики. Эйлер сформулировал его для случая точки, движущейся в поле центральных сил. Точка будет двигаться из данного начального в данное конечное положение таким образом, что для действительного пути 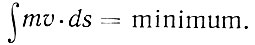Величина mv*ds или mv*dt есть действие. Лагранж обобщил вывод на систему точек.

Таким образом, механика в XVIII в. обогатилась знанием следующих принципов:

1. принцип параллелограмма, или суперпозиции сил (Ньютон, Вариньон, Д'Аламбер);
2. принцип возможных скоростей (И. Бернулли Лагранж);
3. принцип Д'Аламбера (Д'Аламбер, Лагранж);
4. принцип наименьшего действия (Мопертюи, Эйлер, Лагранж). Она уточнила вопрос о мерах движения и их соотношении (Д'Аламбер), выдвинула общий принцип сохранения (Бернулли, Эйлер, Ломоносов).

Особенно важное значение для развития механики имела разработка ее математического аппарата. Ньютон излагал механику громоздким геометрическим методом, не прибегая к созданному им и Лейбницем дифференциальному и интегральному исчислению. Впервые Эйлер в 1736 г. в вышедшей в Петербурге книге "Механика, изложенная аналитически" последовательно применил математический анализ для решения задачи о прямолинейном и криволинейном движении материальной точки. Само понятие материальной точки было введено в науку Эйлером. Уравнение Ньютона для прямолинейного движения Эйлер впервые написал в известной ныне форме

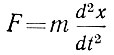
и тем самым свел задачу механики к задаче интегрирования дифференциального уравнения второго порядка. Для криволинейного движения Эйлер ввел разложение ускорения на тангенциальную и нормальную составляющие. В 1742 г. английский математик Маклорен (разложение в ряд функции, носящее его имя, хорошо известно в анализе) в своем курсе математики ("Трактат о флюксиях") ввел разложение движения на три прямоугольных составляющих. Используя прием Маклорена, Эйлер в своей "Теории движения твердых тел" (1765) написал уравнения движения для трех компонентов, которыми и посей день пользуется механика. Особенно важное значение имела разработка Эйлером задачи о движении твердого тела. Им были введены в науку такие понятия, как момент инерции, главные оси инерции, свободные оси вращения. Для характеристики положения тела, вращающегося вокруг неподвижной точки, введены угловые координаты - эйлеровы углы - и написаны уравнения вращения. Основы теории гироскопа, имеющей такое важное научно-практическое значение, были заложены Эйлером. Эйлер написал также уравнения гидродинамики и уравнение гармонической волны, а также уравнение, известное ныне под названием уравнения Лапласа. Таким образом, Эйлер разработал аппарат теоретической физики с такой полнотой, которая заставляет признать его подлинным основателем этой науки.

В 1788 г. вышла "Аналитическая механика" Лагранжа. В этом сочинении Лагранж, продолжая дело Эйлера, разработал математические методы механики с такой общностью, что они в дальнейшем оказались применимыми для решения задач и из других областей физики. Лагранж рассматривает случай системы материальных точек, движения которых подчинены некоторым уравнениям связи. В этом случае движение описывается 3n дифференциальными уравнениями второго порядка для 3n неизвестных функций времени - координат точек. Эти уравнения будут содержать также m неизвестных множителей, определяющих реакции связи, и вместе с присоединенными m уравнениями связи решают задачу. Уравнения, написанные здесь, носят название уравнений Лагранжа первого рода. Следует отметить, что еще ранее, до Лагранжа, они были получены Эйлером.

Но особенно важен второй вид уравнений движения, в которое уравнения связи не входят. Движение характеризуется независимыми обобщенными координатами, число которых равно числу декартовых координат точек системы, за вычетом числа связей. Выражаясь современным языком, число обобщенных координат равно числу степеней свободы системы. Тогда, если число таких координат f и если координаты мы обозначим через q_i, то уравнения движения системы принимают вид

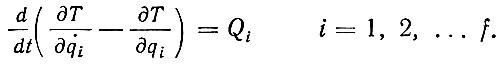
Здесь Т - кинетическая энергия, Q_i - обобщенная сила.

Если силы Q_i имеют потенциал, так что

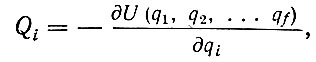
то уравнения Лагранжа принимают вид

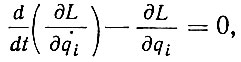
где L = T - U - кинетический потенциал, или функция Лагранжа.

Из сказанного видно, как далеко продвинулась механика в XVIII в. Она сформировалась в мощную, законченную ветвь математической физики и на долгое время отделилась от самой физики, став предметом занятий по преимуществу математиков и специалистов механиков.

Пьер Симон Лаплас

Возникшая из астрономических проблем механика продолжала с успехом заниматься этими проблемами. К достижениям небесной механики этого периода относятся теория движения Луны Эйлера, теория фигуры Земли Клеро (1713-1765), а также блестящее предсказание тем же Клеро появления кометы Галлея. Комета, период которой был предварительно вычислен Галлеем, должна была согласно этому вычислению появиться в 1758 г., однако она в указанный период не появилась. Клеро объяснил это тем, что комета, двигаясь по вытянутому эллипсу, проходила вблизи удаленных больших планет Юпитера и Сатурна, которые возмущали ее движение. По вычислениям Клеро, период должен увеличиться на год и восемь месяцев. Клеро ошибся всего на 22 дня. Это был большой триумф новой науки, триумф теории Коперника - Ньютона. Особенно больших успехов в развитии небесной механики добился Лаплас (1749-1827), первые два тома "Небесной механики" которого вышли в 1799 г. Но Лаплас не только подтвердил и развил теорию Ньютона, он вышел за ее границы. Он отверг гипотезу первого толчка и разработал теорию происхождения солнечной системы. Его предшественником в этом деле был немецкий философ Иммануил Кант (1724-1804). "Всеобщая естественная история и теория неба" И. Канта, носящая подзаголовок "Опыт об устройстве и механическом происхождении всего мироздания на основании ньютониановских законов", появилась в 1755 г. Через 42 года появилось "Изложение системы мира" Лапласа, в седьмом приложении к которому Лаплас изложил гипотезу образования солнечной системы. Основная идея гипотезы Канта - Лапласа - существование первичной туманности, из которой в процессе последовательного вращения в результате взаимодействия гравитационных и отталкивательных сил возникли планеты и спутники. Конечно, одними механическими силами объяснить происхождение солнечной системы невозможно, и гипотеза Канта - Лапласа имеет только историческое значение. Но она, по выражению Энгельса, пробила первую брешь в окаменелом воззрении на природу и открыла путь к решению вопроса об эволюции Вселенной. В этом ее громадное историческое значение.