Оптика

После относительного "затишья" в XVIII в. оптика вновь переживает период бурного развития и напряженной борьбы двух основных оптических теорий: корпускулярной и волновой. Борьба за волновую теорию света была начата в первые же годы нового столетия английским врачом и естествоиспытателем Томасом Юнгом (1773-1829). Юнг выступил в 1800 г. со статьей "Опыты и проблемы по звуку и свету", в которой подвергает критике корпускулярную теорию света и указывает на аналогию звука и света. Рассматривая суперпозицию (наложение) звуковых волн, Юнг указывает, что в результате этой суперпозиции могут происходить как усиления, так и ослабления звука, получаться комбинационные тона и биения. Следовательно, Юнг в отличие от Эйлера принимает во внимание фазовые и частотные соотношения, обусловливающие результат суперпозиции.

В 1801 г. Юнг сформулировал принцип интерференции:

"Везде, где две части одного и того же света попадают в глаз различными путями, либо точно, либо весьма близко по направлению, свет становится более сильным там, где разность путей есть целое кратное некоторой длины, и наименее сильным в промежуточных состояних интерферирующих частей; и эта длина различна для света различных цветов". Эта некоторая длина и есть длина волны, впервые введенная в оптику Юнгом и им же предварительно оцененная из интерференционных опытов. Для получения когерентных пучков ("частей одного и того же света") Юнг воспользовался экраном с двумя малыми близкими отверстиями и получил систему интерференционных полос на приемном экране. С помощью принципа интерференции Юнг объяснил кольца Ньютона, а существование черного пятна в центре колец объяснил изменением фазы ("потерей полуволны") при отражении от оптически более плотной среды. При отражении от менее плотной (в оптическом отношении) среды изменения фазы не происходит, и если показатели преломления линзы, промежуточной среды и подстилающей пластинки в опыте Ньютона расположены в убывающем порядке, то темного пятна в центре не будет. Это заключение Юнг проверил прямым опытом.

Юнг объяснил с помощью своего принципа и дифракционные полосы, наблюдающиеся при получении тени от волоса. Он считал, что дифракционные полосы вне тени образуются в результате интерференции прошедшего света со светом, отраженным от краев волоса, а внутренние полосы интерференцией лучей, дифрагирующих у краев тени. Для экспериментального подтверждения этой идеи он приставил к краю волоса полоску непрозрачной бумаги и показал, что в этом случае внутренние полосы исчезают. Юнг восстановил принцип Гюйгенса для объяснения распространения света в кристалле исландского шпата и обратился к известному английскому физику-экспериментатору Волластону (1766-1828) с просьбой экспериментально проверить значения показателей преломления, даваемые построением Гюйгенса. Опыты Волластона (1802 г.) подтвердили теорию Гюйгенса. Однако именно в вопросе о распространении света в кристаллах волновая теория Юнга встретилась с серьезными трудностями.

В 1808 г. французский военный инженер Малюс (1775-1812) наблюдал через кристалл исландского шпата отражение лучей заходящего солнца в стеклах Люксембургского дворца и заметил исчезновение одного из двух лучей, получающихся при преломлении в исландском шпате. Последующие измерения с отражением света от свечи в воде показали, что это исчезновение наблюдается при определенных углах отражения. Малюс пришел к выводу, что отраженный луч обладает особой ассимметрией вокруг своего направления, и назвал это свойство луча поляризацией.

В последующие годы были открыты: хроматическая поляризация (Араго, Брюстер, 1813 г.), двухосные кристаллы (Био, Брюстер, 1812 г.), вращение плоскости поляризации (Араго, 1811 г., Био, 1815 г.), хроматическая поляризация в двухосных кристаллах (Брюстер, 1813-1818 гг.). Эти сложные явления никак не объяснялись волновой теорией Юнга, принимавшей, что световые волны, подобно акустическим в воздухе, продольные. Эфир рассматривался как сверхтонкий газ, обладавший определенной упругостью и плотностью, и скорость световых волн определялась формулой:

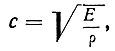
где Е - модуль упругости, ρ - плотность эфира. Для продольных волн никакой асимметрии вокруг луча быть не должно: все плоскости, содержащие луч, равноправны. Лапласу же удалось построить математическую теорию распространения света в кристалле, исходя из корпускулярных представлений о свете. Био обобщил эту теорию на двухосные кристаллы. Теория Юнга была забыта, но ненадолго. Знаменитый французский физик О. Френель (1788-1827) создал классическую волновую оптику.

Огюстен Жан Френель

15 октября 1815 г. Френель представил Парижской Академии наук первый мемуар о дифракции света. В этом и последующих мемуарах Френель описывает свои классические опыты по дифракции на конечных расстояниях от источника и их теоретическое истолкование на языке волновой теории. В основу теории дифракции Френель кладет принцип Гюйгенса, дополняя его гипотезой об интерференции вторичных лучей, исходящих из точек волнового фронта. Для приближенного расчета дифракционной картины Френель предложил метод зон. Чтобы рассчитать действие волнового фронта на данную точку, из этой точки описывается сфера с последовательными радиусами r₁ = d, r₂ = d + ^λ/₂, r₃ = d + λ, r₄ = d + ^3λ/₂ и т. д., где d - наименьшее расстояние волновой поверхности от приемной точки, и затем рассматривается суммарное воздействие полученных зон на эту точку. Несмотря на то что этот метод страдает существенными недостатками (неправильная фаза, трудность с объяснением отсутствия обратной волны), он дал в руках Френеля необычайно ценные результаты. Из способа подсчета Френеля вытекало (на это следствие указал противник волновой теории Пуассон), что в центре тени от малой круглой ширмы всегда должен быть свет. Араго подтвердил этот вывод прямым экспериментом, и возражение Пуассона превратилось в доказательство справедливости принципа Гюйгенса - Френеля. В 1816 г. Френель осуществил классический интерференционный опыт с двумя зеркалами, о котором он сам пишет, "что лишь теория колебаний могла привести к идее постановки таких опытов. Этот опыт настолько труден, что почти невозможно, чтобы чистый случай на него натолкнул". Волновая теория позволила, таким образом, предугадать результаты опытов, которые без их тщательного обоснования, вероятно, никогда бы не были осуществлены. Но перед волновой теорией стояла труднейшая задача - истолковать поляризационные явления. И здесь Френель сделал необычайно смелый шаг. Основываясь на том опытном факте, что луч обыкновенный и необыкновенный, даже если их привести к одной плоскости поляризации, не интерферируют, он ввел гипотезу о поперечности световых колебаний. Это была очень смелая идея, так как в газах и жидкостях (а эфир считался чрезвычайно тонкой жидкостью или газом) поперечные волны невозможны, они возможны только в твердых телах. Таким образом, гипотеза Френеля наделяла эфир противоречивыми механическими свойствами. Тем не менее Френель ввел эту гипотезу и с ее помощью объяснил явления поляризации, дал теорию распространения света в кристаллах, как одноосных, так и двухосных, объяснил вращение плоскости поляризации допущением разложения поляризованного света в оптически активных средах на две составляющие поляризованные по кругу в противоположных направлениях, и распространения света в этих средах с разными скоростями. Свою теорию вращения плоскости поляризации Френель подтвердил опытом с кварцевой призмой, изготовленной из правовращающего и левовращающего кцарца. Френель нашел также законы отражения и преломления, исходя из гипотезы, что упругость эфира в веществе не меняется, а меняется только плотность. Предполагая, что плоскость световых колебаний перпендикулярна плоскости поляризации, и применяя закон непрерывности колебания при переходе через границу и закон сохранения "живых сил", Френель получил свои известные формулы для амплитуд преломленной и отраженной волны. Далее Френель рассмотрел явление полного отражения, смело введя для математического описания этого явления комплексные числа. Полученные им результаты дали ему возможность изготовить прибор, позволяющий преобразовать линейную поляризацию в круговую и обратно с помощью полного отражения (параллелепипеда Френеля). Наконец, Френель рассмотрел вопрос о влиянии движения среды на распространение света и пришел к выводу, что движущиеся тела частично увлекают эфир. Если тело движется со скоростью v, то эфир движется со скоростью v₁ = kv, где k = 1 - ¹/_n² - френелевский коэффициент увлечения. Этот результат Френеля был позже подтвержден экспериментально Физо, Эри, Майкельсоном и сыграл важную роль в истории принципа относительности.

Большим успехом теории двойного преломления Френеля был теоретический вывод из нее ирландским астрономом и механиком Гамильтоном (1832 г.) конического преломления лучей, когда луч, падающий на пластинку двухосного кристалла, вырезанную соответствующим образом, расщепляется на конус лучей. Это тонкое явление было экспериментально найдено Ллойдом через год после расчета Гамильтона.

В те же годы, когда Френель начал разрабатывать волновую теорию света, немецкий оптический мастер Фраунгофер (1787-1826) начал тщательные исследования солнечного спектра. Он нашел и точно зафиксировал в призматическом спектре Солнца черные линии - фраунгоферовы линии. Эти линии наблюдались еще в начале века Волластоном, но последний не стал их подробно описывать, считая это бесполезным. После того как Фраунгофер в 1814-1815 гг. описал темные линии в спектре Солнца, он перешел к получению дифракционных спектров, сначала от щели, а потом с помощью изобретенного им нового спектрального аппарата - дифракционной решетки (1822 г.). С помощью дифракционных спектров Фраунгофер измерил длины волн, соответствующие темным линиям спектра. Эти исследования положили начало спектроскопии. Теория дифракционной решетки Фраунгофера была дана Швердом в 1835г.

Крупным успехом оптики, правда, относящимся уже к середине XIX в., было измерение скорости света земными методами Физо (1849 г.) и Фуко (1850 г.). Последний доказал, что скорость света в воде меньше, чем скорость света в воздухе, что подтверждало выводы Гюйгенса и противоречило выводам Ньютона. Таким образом, к середине XIX в. волновая оптика победила, как казалось, окончательно. Но ее победа принесла и немалые трудности, вызвав целый ряд неудачных попыток построить непротиворечивую механическую теорию эфира.

Вместе с тем волновая теория поляризации света, созданная Френелем, стимулировала развитие теории упругости, в особенности теорию распространения волн в упругой среде. Эту теорию разрабатывали Коши и Пуассон. Коши сделал свое первое сообщение в сентябре 1822 г. Уравнения теории упругости были опубликованы им в 1828 г. В том же году появилась работа Пуассона. Исследования Коши и Пуассона основывались на представлении о молекулярных силах, действующих между частицами упругого тела. В дальнейшем ими, а также Ламе и Клапейроном аналогичный метод был применен к решению задач упругих колебаний и равновесий. Коши применил найденные им уравнения к распространению света как в кристаллических, так и изотропных телах (1830 г.). Теорию Коши Грин применил в 1839 г. к явлениям отражения и преломления на границе двух некристаллических сред. Существенно, что Грин применил здесь новый метод вывода уравнений упругости, основанный на идее сохранения энергии. Функция, введенная Грином, есть не что иное, как взятая с обратным знаком потенциальная энергия единицы объема деформированного тела, выраженная через компоненты деформации. Эти исследования сыграли большую роль в развитии математического аппарата волновой оптики и подготовили почву для электромагнитной теории света Максвелла.