Статистическая физика

Открытие механического эквивалента теплоты приводило к выводу, что теплота является видом механического движения. Этот вывод сделал сам автор опытов по определению механического эквивалента теплоты Джемс Джоуль, доложивший 30 октября 1848 г. Манчестерскому философскому обществу "Некоторые замечания о теплоте и о строении упругих жидкостей". Здесь он, отправляясь от своих опытов, обсуждает идею о том, что упругость газа представляет собою эффект движения частиц, из которых состоит всякий газ. Родоначальником этой гипотезы Джоуль называет Дэви, считавшего, что теплота обусловлена вращательным движением частиц тела. Эту гипотезу Джоуль называет "прекрасной" и прибавляет: "Я лично попытался показать, что вращательное движение, аналогичное описанному сэром Дэви, способно объяснить закон Бойля и Мариотта, а также и другие явления, представляемые другими жидкостями"^*. Как мы знаем, такую гипотезу и ее применение к явлениям теплоты и упругости газов впервые выдвинул М. В. Ломоносов за сто лет до Джоуля. Джоуль об этой гипотезе не упоминает, так же как и не упоминает позже Клаузиус, перечисляющий всех своих предшественников вплоть до древних атомистов. Этот факт забвения достижений русских ученых неоднократно встречается в истории западной науки. В указанной статье Джоуль, однако, рассматривает не гипотезу Дэви, а гипотезу Герапата о поступательном движении частиц и обосновывает этой гипотезой закон Бойля-Мариотта и зависимость скоростей газа от температуры. Он пытается также вычислить удельные теплоемкости газов, но полученные им значения для водорода, кислорода, азота и углекислоты сильно расходились с опытными данными Делароша и Берара. Вопрос о причине этих расхождений он оставляет открытым до опубликования экспериментальных результатов Реньо.

^* ("Основатели кинетической теории материи", сборник под ред. А. К. Тимирязева, ОНТИ, 1937, стр. 36.)

В 1856 г. появляется работа Кренига "Основы теории газов", в которой вычисляется давление газа из гипотезы молекулярного движения. Крениг ошибочно полагает, что молекула отдает стенке сосуда свой импульс, и потому в его формуле давление получается вдвое меньше действительной величины. Однако пропорциональность давления кинетической энергии молекул устанавливается.

В 1857 г. появляется первая статья по кинетической теории газов Клаузиуса "О роде движения, который мы называем теплотой". В переработанном виде статьи Клаузиуса составили третий том его "Механической теории тепла" В работах Клаузиуса ясно выступает идея о статистическом характере газовых законов, состояние газа, его температура и давление определяются средними значениями кинетической энергии молекул. Введя в гипотезу, что для идеальных газов объем, занимаемый молекулами, пренебрежимо мал, время столкновения исчезающе мало по сравнению с промежутком времени между двумя столкновениями и что влиянием молекулярных сил можно пренебречь, Клаузиус вычисляет давление газа и находит известное соотношение

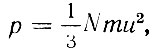
где N - число молекул в единице объема, m - масса одной молекулы, u² - средний квадрат скорости движения молекул. Клаузиус дал кинетическую модель трех агрегатных состояний вещества и нарисовал молекулярный механизм испарения. Им было также положено начало молекулярной теории теплоемкости газов.

В работе "О средней длине пути молекул газа" (1858 г.) Клаузиус показывает, каким образом можно примирить кажущееся противоречие между относительно большими средними скоростями молекул (нередко нескольких сотен метров в секунду при комнатных температурах) с наблюдающимися на опыте малыми скоростями диффузии. Здесь Клаузиус вводит новую важную характеристику молекулярного мира: среднюю длину свободного пробега. При вычислении этой величины Клаузиус исходит из предположения, что средняя квадратичная скорость одинакова у всех молекул данного газа.

21 сентября 1859 г. Д. К. Максвелл сделал доклад на съезде Британской Ассоциации в Абердине под названием "Пояснения к динамической теории газов". В этом докладе содержится дальнейшее развитие кинетической теории газов. Рассматривая модель газа в виде системы огромного количества упругих шариков, Максвелл устанавливает, что в результате взаимных столкновений между этими шариками в конечном счете получается некоторое стационарное распределение скоростей, так что при данной температуре скорость группируется вокруг некоторой наивероятнейшей скорости. Оказывается, "что скорости распределяются между частицами по тому же закону, по которому распределяются ошибки между наблюдениями в теории наименьших квадратов"^*. Это чисто статистический закон: методы теории вероятностей проникли в физику. Максвелл рассматривает далее так называемые "явления переноса", возникающие тогда, когда в дополнение к скоростям теплового движения, равномерно распределенным по всем направлениям, существует и общее движение переноса всей системы частиц. К таким явлениям относится явление внутреннего трения, или вязкости, явление диффузии, явление теплопроводности. Максвелл получил из своей теории результат, что коэффициент трения не зависит от плотности. "Этот вывод из математической теории является крайне поразительным,- писал Максвелл,- и единственный опыт, с которым я встретился в этой области, как будто его не подтверждает"^**. Однако последующие эксперименты Кундта и Варбурга блестяще подтвердили вывод теории, и независимость коэффициента трения газов от давления подтверждается до давлений 0,63 мм рт. ст. В разреженных газах начинаются отступления от этого закона, объясняемые, как показали в 1875 г. Кундт и Варбург, скольжением молекул газа вдоль стенок. Явление скольжения газа при больших разрежениях исследовал экспериментально и теоретически профессор Московского университета А. К. Тимирязев (1880-1955) в 1913-1917 гг. Экспериментальная проверка кинетической теории газов имела очень важное значение для прогресса науки. Против атомно-молекулярной гипотезы выступил ряд ученых (Мах, Оствальд и другие), считавших, что наука не должна иметь дела с "ненаблюдаемыми" величинами. Это было продолжение старой борьбы ньютонианцев против материалистических гипотез.

^* ("Основатели кинетической теории материи", сборник под ред. А. К. Тимирязева, ОНТИ, 1937, стр. 192.)

^** ("Основатели кинетической теории материи", сборник под ред. А. К. Тимирязева, ОНТИ, 1937, стр. 203.)

Однако физики-материалисты продолжали пользоваться молекулярными представлениями, оценивали такие молекулярные величины, как длину свободного пробега, диаметр молекул, число молекул в единице объема и т. д., находили связи между отдельными коэффициентами вещества: коэффициентом теплопроводности, вязкости, диффузии. В 1873 г. Ван-дер-Ваальс сделал попытку учесть силы сцепления между молекулами и их собственный объем и таким путем, применяя молекулярно-кинетические соображения, пришел к уравнению состояния реальных газов, о котором говорилось в предыдущем разделе. В 1865 г. австрийский физик Лошмидт (1821- 1895) сделал первую попытку подсчитать число молекул на основе измерений длины свободного пробега и отношения плотностей жидкости и газа. В честь этого первого определения число молекул в единице объема называют числом Лошмидта.

Кинетическая теория газов привела к физическому истолкованию температуры как меры энергии движения молекул. Перед механической теорией теплоты стояла дальше задача свести к механическим образам второе начало термодинамики. Решением этой задачи занимались многие физики, в том числе Больцман, Клаузиус и Гельмгольц. Исходя из того, что для обратимых процессов можно определить функцию состояния посредством равенства 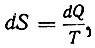они искали такого механического обоснования этого соотношения, которое давало бы автоматически интегрирующий делитель для количества теплоты.

Людвиг Эдуард Больцман

Но суть второго начала - именно в необратимости термодинамических процессов, в констатации определенной направленности природных процессов, в принципе одностороннего изменения энтропии. Заслуга физического истолкования второго начала и энтропии и вместе с тем введения статистического метода в физику принадлежит австрийскому ученому Людвигу Больцману (1844-1906). Метод рассмотрения явлений природы Больцмана, который он сам называл механическим, противопоставляя его термодинамическому (называемому им феноменологическим), заключался в рассмотрении большого количества частиц, движущихся и взаимодействующих между собой по законам механики, но в силу полной нерегулярности начальных условий, находящихся в состоянии "молекулярного хаоса". Можно поставить вопрос о распределении молекул по состояниям, причем состояние характеризуется в механическом смысле координатами и импульсами частицы. Рассматривая так называемый фазовый объем, определенный каким-либо заданным интервалом координат и импульсов, можно поставить вопрос о распределении молекул по фазовым объемам. Больцман показал, что в данных внешних условиях (в данном силовом поле, при данной температуре и в данном объеме газа) в результате взаимных столкновений устанавливается определенное стационарное распределение, характеризующееся функцией вида Ае^-сЕ, где Е - полная энергия молекулы, с - постоянная, зависящая от температуры (обратно пропорциональная абсолютной температуре). Это так называемое распределение Максвелла - Больцмана; оно содержит, в частности, закон максвелловского распределения скоростей. Больцман установил также, что в установившемся состоянии количество молекул, кинетическая энергия их движения распределяются равномерно по степеням свободы так, что на каждую степень свободы молекулы приходится одна и та же кинетическая энергия, пропорциональная абсолютной температуре (¹/₂)kT, где k - новая константа молекулярного мира, называемая "постоянной Больцмана", хотя она была впервые введена и определена Планком). Наконец, в 1877 г. Больцман дал статистическое истолкование второго закона термодинамики и энтропии. Рассматривая данную физическую систему, находящуюся в определенном состоянии, характеризуемом распределением молекул по фазовому объему, он наряду с этой системой рассматривал также все физически возможные копии ее и находил наивероятнейшее состояние системы. Для газа это наивероятнейшее распределение опять-таки оказывалось максвелл-больцмановским распределением. Введя функцию Я, пропорциональную отрицательному значению логарифма функции распределения, Больцман показал, что система всегда будет переходить в такое состояние, при котором Н уменьшается. Он сопоставил этот результат с фактом одностороннего изменения энтропии и отождествил эту последнюю с отрицательным значением Я. Таким образом, тот факт, что в замкнутой системе энтропия возрастает, означает просто, что система стремится к наиболее вероятному состоянию. Связь между энтропией и вероятностью состояния (в форме, позже приданной ей Планком)

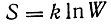
является одним из важнейших результатов теоретической физики. Этот результат неоднократно оспаривался рядом ученых (Пуанкаре, Цермело и др.), но последующее развитие физики полностью подтвердило правоту Больцмана. Метод статистической механики, развитый Больцманом, был в дальнейшем обстоятельно разработан американцем Д. В. Гиббсом, классический труд которого "Основные принципы статистической механики" вышел в 1902 г. Следует отметить, что в статистической механике, так же как позднее в атомной механике, чрезвычайно важное значение получил аппарат аналитической механики, созданной в первой половине XIX в. ирландским математиком и астрономом Вильямом Гамильтоном.

В методе Гиббса, обладающем чрезвычайной абстрактностью и общностью, механическая система рассматривается как совокупность N объектов (например, молекул), каждый из которых обладает f степенями свободы и механическое поведение которого описывается 2f уравнениями Гамильтона. Совокупность 2Nf переменных рассматривают как координаты в некотором 2Nf-мерном фазовом пространстве и состояние системы в данный момент рассматривают как "точку" в этом пространстве. Затем подразделяют фазовое пространство на произвольные элементы и рассматривают распределение фазовых точек по этим элементам. Из законов, найденных Гиббсом, получаются результаты Больцмана о равномерном распределении энергии по степеням свободы, о стационарном и наивероятнейшем распределении Максвелла-Больцмана и т. д.

Анализ принципов статистической механики дали работавшие в Петербурге физики П. С. Эренфест и его жена Т. А. Афанасьева-Эренфест.

Жан Перрен

Из того факта, что состояние термодинамического равновесия является только наивероятнейшим, следует, что мыслимы отступления от этого состояния "флюктуации". Анализом максвелл-больцмановского распределения и флюктуации занимался русский физик, сын известного хирурга и педагога Н. И. Пирогова, Николай Николаевич Пирогов (1843-1891). Им, в частности, была получена формула для оценки колебаний числа молекул в заданном объеме газа, позже найденная польским физиком Марианом Смолуховским (1872-1917). Смолуховскому и Альберту Эйнштейну принадлежит анализ такого классического флюктуационного явления, как броуновское движение. Результаты, полученные Эйнштейном в 1905 г., послужили теоретической основой экспериментальных работ французского физика Жана Перрена (1870-1942), в которых впервые прямым методом была определена важная молекулярная постоянная - число Авогадро - и, следовательно, дан метод непосредственного определения размеров молекул. Аргументация махистов и энергетиков, что атомы и молекулы из-за своей недоступности прямым измерениям являются такими же призраками, как ведьмы, была бита. К сожалению, Больцману не пришлось дожить до своего триумфа, тяжелая борьба надломила его нервную систему, и в 1906 г. он покончил самоубийством. В более поздних работах Смолуховского были воочию продемонстрированы случаи отступления от второго закона и определена вероятность таких случаев. И уже через год после смерти Больцмана, в 1907 г., знаменитый голландский физик Г. А. Лорентц говорил в речи, посвященной памяти Больцмана, в связи с растущим накоплением экспериментального материала, свидетельствующего о правильности атомно-молекулярного учения:

"Какой картине следует отдать предпочтение, с какой можно идти дальше, в этом Больцман никогда не сомневался. Неоднократно он возвращался к той мысли, что без молекулярной, или атомистической, теории многое, как например законы химических соединений, основной закон кристаллографии, а в физике независимость трения в газах от плотности, связь между трением, теплопроводностью и диффузией, остается непонятным. Также сильным аргументом в пользу молекулярной теории для него являлось совпадение значений молекулярных величин, найденных различными путями. К приведенному Больцманом можно еще прибавить многое другое, например открытую Нернстом связь между коэффициентом диффузии электролитов и их электрическими свойствами; многие результаты современной электронной теории и теории излучения; определение Д. Д. Томсоном электрического заряда газовых ионов с помощью его метода тумана; данное Майкельсоном доказательство, что ширина наиболее тонких спектральных линий может быть объяснена, согласно принципу Допплера, из молекулярного движения; обнаруженный Штарком эффект Допплера для каналовых лучей. Учет всех этих результатов может даже, как мне кажется, привести нас к тому, чтобы совсем отбросить осторожные оговорки, которыми Больцман обычно выражался. Реальное существование молекул и атомов, при сопоставлении всего этого, представляется установленным едва ли менее надежно, чем действительное существование железа в солнечной атмосфере".

Нам, живущим в эпоху торжества атомной науки, кажется непостижимым, что было такое время, когда ученые сомневались в существовании атомов и молекул. Трагическая судьба Больцмана напоминает нам, что атомное учение развивалось в жестокой борьбе. Через три года после кончины Больцмана глубокое философское значение этой борьбы раскрыл В. И. Ленин в своем знаменитом произведении "Материализм и эмпириокритицизм". В этом произведении он дал обстоятельный критический анализ взглядов противников атомистики и философского материализма: махистов, энергетиков, позитивистов, эмпириокритиков, всех тех, кто тормозил развитие передовой, материалистической науки. Ленин указал путь преодоления всех и всяческих кризисов науки.