Изменения во взглядах на пространство и время. Теория относительности

Как известно, Ньютон допускал объективное существование однородного и изотропного абсолютного пространства, не связанного с материей и существующего независимо и безотносительно к материальным вещам. Движение тела относительно этого пространства абсолютное, ибо ньютоновское абсолютное пространство неподвижно. Это пространство эвклидово, и свободная материальная точка движется в нем равномерно и прямолинейно. На практике мы имеем дело с относительными движениями и можем принимать в качестве системы отсчета любое тело. Систему отсчета, связанную с центром тяжести солнечной системы и с осями, направленными к неподвижным звездам, Эйнштейн предложил называть галилеевой, так как по отношению к этой системе с достаточной точностью выполняется закон инерции: свободная точка движется равномерно и прямолинейно. Галилеева система поэтому называется также инерциальной. По принципу относительности Галилея-Гюйгенса-Ньютона существует бесчисленное множество равноправных инерциальных систем, находящихся в состоянии равномерного прямолинейного движения друг относительно друга, так что никаким механическим опытом нельзя определить, находится ли инерциальная система в состоянии покоя или движется равномерно и прямолинейно. При этом предполагается, что время является абсолютным, т. е. текущим одинаково для всех систем отсчета. Абсолютное пространство Ньютона приобрело материальную форму с момента утверждения волновой оптики, оно слилось с всепроникающим мировым эфиром. Поэтому появилась возможность установить экспериментально абсолютное движение, производя оптические эксперименты с движущимися телами. Вопрос о влиянии движения системы на распространение света был поставлен еще Юнгом. В 1804 г. Юнг дал объяснение явлений аберрации света с точки зрения волновой теории. Сущность этого объяснения заключается в гипотезе, что эфир не принимает участия в движении Земли. В 1818 г. Френель исследует вопрос о движении эфира в связи с отрицательным результатом опыта Араго, пытавшегося обнаружить влияние движения Земли на показатель преломления. Он ввел гипотезу о частичном увлечении эфира движущимися телами. Найденное Френелем значение коэффициента увлечения k = 1 - ¹/_n² было подтверждено на опыте Физо в 1851 г. Физо сравнивал скорость света в движущейся и неподвижной воде. Его опыт был повторен Майкельсоном в 1878 г., который пришел к тому же результату. В 1871 г. Эри наблюдал аберрацию через телескоп, труба которого была заполнена водой: никакого изменения угла аберрации не происходило. Этот результат может быть истолкован с помощью гипотезы о частичном увлечении эфира.

После утверждения электромагнитной теории света вопрос о влиянии движения на эфир получил более широкое значение, так как эфир является теперь ареной не только оптических, но и электрических процессов. С точки зрения максвелловской электродинамики, полный индукционный процесс в среде характеризуется векторами D и B, а силовое поле в чистом эфире - векторами Е и H. При движении тел возможно участие в этом движении, кроме заряженных частиц этих тел, и эфира, и тогда вместе с телом движется полный поток линий индукции, характеризуемый векторами D и В. Если же эфир неподвижен, то та часть потока, которая обусловлена процессом в чистом эфире и характеризуется векторами Е и Н, не принимает участия в движении, движутся только заряженные или намагниченные частицы вещества. Герц (1890 г.) предположил, что эфир полностью увлекается движущимися телами. В этом случае уравнения Максвелла в движущейся среде имеют такую же форму, как и в неподвижной среде, и, таким образом, удовлетворяют принципу относительности Галилея-Гюйгенса-Ньютона. Электродинамические, а следовательно, и оптические опыты не дают возможности, как и механические опыты, обнаружить движение системы. Правда, Герц оговаривался, что его теория не применима к оптическим явлениям, а только к чисто электромагнитным. Однако и в области электродинамики, как оказалось, теория Герца противоречит опыту.

Гендрик Антон Лорентц

В 1895 г. теорию электродинамических и оптических явлений в медленно движущихся средах разработал Гендрик Антон Лорентц (1853-1928). Критерием "медленности" движения служит отношение β = ^υ/_c. Если оно настолько мало, что квадратом этой величины можно пренебречь по сравнению с единицей, то движение считается медленным. Лорентц предполагает, что эфир неподвижен и что, следовательно, возможно говорить об абсолютном движении относительно эфира. Поэтому различные системы отсчета не будут равноправными относительно друг друга, они различаются скоростью относительно эфира. Но это различие, как показал Лорентц, будет сказываться только в членах второго порядка относительно р. Если точность опытов такова, что можно оценить только члены первого порядка величины Р, то неравноправия движущихся систем обнаружить нельзя - это так называемый принцип относительности первого порядка Лорентца.

В теории Лорентца коэффициент увлечения Френеля k = 1 - ¹/_n² обусловлен тем, что движутся заряженные частицы (френелева "сгущенная" часть эфира), и, следовательно, опыт Физо получает естественное истолкование.

Теории Герца и Лорентца приводят к следствиям, доступным экспериментальной проверке. Если движется заряженный проводник по отношению к стенам лаборатории ("лабораторная система отсчета"), то возникает магнитное поле, пропорциональное заряду проводника и скорости движения. Этот вывод одинаково следует и из теории Герца и из теории Лорентца. Он был проверен экспериментально Г. А. Роуландом (1878 г.), Рентгеном (1895 г.) и наиболее точно русским физиком А. А. Эйхенвальдом (1863-1944).

Если привести в движение диэлектрик, то из теории Герца следует, что такой диэлектрик будет создавать магнитное поле, пропорциональное вектору электрической индукции D и скорости диэлектрика v. Теория Лорентца приводит к другому результату, а именно - магнитное поле будет пропорционально вектору поляризации Р и скорости движения. Таким образом, ток диэлектрика в теории Герца пропорционален D*v, а в теории Лорентца пропорционален P*v

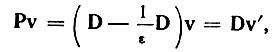
где

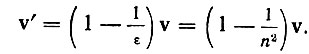
Таким образом, в теории Лорентца так называемое "увлечение" эфира является результатом движения зарядов в неподвижном эфире. Магнитное поле движущегося диэлектрика наблюдали Рентген и А. А. Эйхенвальд. Опыты Эйхенвальда подтвердили теорию Лорентца.

Александр Александрович Эйхенвальд

Теория Герца противоречит также аберрационному опыту и опыту Физо. Теория Лорентца с этими опытами согласуется. Однако теория Лорентца допускает возможность обнаруживания во втором порядке абсолютного движения системы отсчета относительно эфира. На такую возможность указал еще в 1879 г. Максвелл в письме к редактору английского журнала "Природа". Это письмо было опубликовано в журнале уже после смерти Максвелла в январе 1880 г. и было прочитано молодым американским физиком Альбертом Майкельсоном (1852-1931). Уже в следующем году Майкельсон поставил свой знаменитый опыт с интерферометром. Опыт дал отрицательный результат. Свет распространялся в лаборатории в соответствии с теорией Герца и принципом относительности одинаково во всех направлениях. Так как в расчеты Майкельсона вкралась ошибка, на которую ему указал Лорентц в 1884 г., то Майкельсон вместе с Морлеем (Морли) повторил опыт в 1887 г., значительно повысив точность эксперимента. Опыт вновь дал прежний результат, противоречащий теории неподвижного эфира Лорентца.

В 1891 г. английский физик Фицджеральд (1851-1901) и независимо от него Г. А. Лорентц в 1892 г. предложили теорию, объясняющую результат Майкельсона. Твердые тела, согласно этой теории, деформируются вследствие движения, а именно испытывают в направлении движения сокращение в отношении 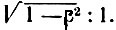Лорентц в дальнейшем обосновал свою гипотезу, исходя из того, что молекулярные силы, определяющие упругие свойства тел, электромагнитного происхождения и в соответствии с его теорией должны зависеть от абсолютного движения через эфир. По Лорентцу, деформируются и электроны, что, в свою очередь, приводит к зависимости их электромагнитной массы от скорости. Впервые понятие электромагнитной массы было установлено Д. Д. Томсоном в 1881 г., и он же нашел, что она зависит от скорости. В 1889 г. понятие электромагнитной массы разбирал О. Хевисайд, затем М. Абрагам (1902) и Лорентц. Электромагнитная масса должна зависеть от скорости, характер этой зависимости определяется гипотезой о структуре электрона. Абрагам считал электрон твердым шариком. Лорентц - деформирующимся. В 1901 г. В. Кауфман начал эксперименты с отклонением β-частиц в магнитном поле и обнаружил зависимость массы этих частиц от скорости. Продолжая свои исследования, он показал, что они говорят в пользу гипотезы Лорентца.

Из теории Лорентца вытекала возможность других опытов второго порядка. Одним из таких опытов был опыт с конденсатором, поставленный Троутоном и Ноблем в 1904 г. Если существует абсолютное движение заряженного конденсатора через эфир, то он должен испытывать вращательный момент, зависящий от угла между направлением силовых линий в конденсаторе и скоростью его движения (N = Wβ²*sin 2α, где W - электростатическая энергия конденсатора, 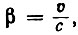α - угол между направлением поля и скоростью движения).

Опыт Троутона-Нобля также дал отрицательный результат. Другим методом определения движения относительно эфира мог бы служить метод, основанный на изменении частоты колебаний при движении источника света или наблюдателя. Акустический эффект Допплера (1842 г.), как известно, зависит не только от относительной скорости источника и наблюдателя, но и от скорости одного из них относительно воздуха. Но существование оптического эффекта Допплера оспаривалось, несмотря на подтверждение этого принципа в акустике. Впервые существование этого эффекта было доказано в астрофизике (Хюггинс, 1868 г.). В. Вин использовал принцип Допплера для обоснования своего закона смещения. В 1900 г. русский астрофизик А. А. Белопольский экспериментально обнаружил спектральное смещение, обусловленное движением, применив остроумный метод многократного отражения луча светод многократного отражения луча света от движущихся зеркал, и подтвердил его совпадение с расчетом по формуле Допплера. В 1899 г. появилась работа В. А. Михельсона, в которой он, указывая на трудности, связанные с применением эффекта Допплера в оптике, показал, в частности, что смещение линий может быть обусловлено и быстрым изменением плотности среды, в которой распространяется свет^*. В 1905 г. Штарк воспользовался эффектом Допплера для измерения скоростей каналовых лучей. В 1907 г. Б. Б. Голицын и Вилип подтвердили методом Белопольского формулу Допплера. Однако точность этих измерений была недостаточна, чтобы можно было сделать вывод о движении относительного эфира. Тем не менее эксперименты подтвердили гипотезу Допплера: независимость скорости распространения света от движения источника. Следовательно, опыт Майкельсона указывает на независимость скорости света от движения системы отсчета, эффект Допплера указывает на ее независимость от движения источника. В 1908 г. В. Ритц пытался объяснить отрицательный результат опыта Майкельсона гипотезой о зависимости скорости света от движения источника, как это имеет место в теории истечения. Но по теории истечения могут быть различные истолкования эффекта Допплера и различные результаты в зависимости от принятых гипотез.

^* (В 1901 г. эта работа Михельсона была опубликована на английском языке.)

Альберт Майкельсон

Опыты Белопольского и Голицына подтверждают выводы волновой теории. Теория Ритца дает результат, отличающийся от теории Допплера в членах второго порядка, и потому не противоречит опытам Белопольского и Голицына. Но Де-Ситтер в 1913 г. показал, что выводы теории Ритца уже в первом порядке противоречат наблюдениям над двойными звездами. Эти наблюдения подтверждают факт независимости скорости света от движения источника. Но это означает, что дифференциальное уравнение распространения световой волны

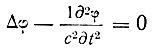
должно сохранять свою форму для всех движущихся равномерно и прямолинейно относительно эфира систем отсчета. В 1887 г. В. Фогт в статье "О принципе Допплера" указал, что для этого необходимо изменить формулы преобразования таким образом, чтобы при переходе от одной системы отсчета к другой преобразовывались не только координаты, но и время. Идею "местного времени", преобразующегося при переходе от одной системы отсчета к другой, развил и Лорентц в своих работах 1892 и 1895 гг. Но у Фогта и Лорентца при преобразованиях масштаб времени не меняется. Впервые формулы преобразования координат и времени с изменением масштаба последнего были даны Д. Лармором в книге "Эфир и материя" в 1900 г. В 1904 г. в классической работе "Электромагнитные явления в системе, движущейся со скоростью меньшей, чем скорость света" Лорентц доказывает, что уравнения Максвелла, а следовательно, и законы распространения света во всех системах отсчета, движущихся равномерно и прямолинейно относительно эфира, остаются инвариантными, если формулы преобразования координат и времени имеют вид:

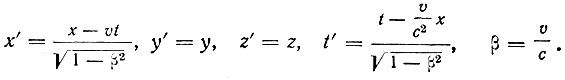
Это знаменитые преобразования Лорентца. При этом Лорентц не говорит о принципе относительности как всеобщем законе природы, преобразование времени является лишь необходимым формальным приемом, сохраняется привилегированная система отсчета (эфир), и сокращение размеров тел при движении относительно эфира рассматривается как результат изменения электромагнитных сил вследствие движения. В следующем, 1905 г. с большой работой "О динамике электрона" выступил французский математик и астроном А. Пуанкаре (1854-1912). Здесь Пуанкаре высказывает в виде общего принципа постулат относительности и рассматривает группу преобразований Лорентца. То, что Пуанкаре рассматривал вопрос о преобразованиях Лорентца с точки зрения теории групп (абстрактной и сложной математической теории), сделало его работу недоступной для большинства физиков. К тому же, разработав полно и широко математический аппарат специальной теории относительности, Пуанкаре остановился на полдороге перед общефизическими выводами из теории, сделав вопрос о пространстве и времени предметом "соглашения", "условия" (конвенционализм).

Альберт Эйнштейн

В том же, 1905 г. молодой физик А. Эйнштейн (1879-1955) выступил со статьей "К электродинамике движущихся тел", в которой с большой ясностью, простотой и глубиной решил запутанную проблему. Основная идея этой работы заключается в том, что надо раз и навсегда отказаться от попыток определения абсолютного движения и отбросить ньютоновские понятия абсолютного пространства и времени, как не имеющие реального физического смысла. Физические понятия о времени и пространстве образуются из реальных процессов и отношений материальных тел. Время - это, так сказать, совокупность "часов", а пространство - совокупность "масштабов". Хотя философская позиция самого Эйнштейна не отличалась четкостью, он сильно склонялся к махизму и нередко делал идеалистические выводы из своих физических идей, однако сами его идеи свидетельствуют о наличии стихийной материалистической диалектики в его физических воззрениях. Напомним, что еще Энгельс в "Диалектике природы", критикуя Негели за неспособность найти правильное соотношение между эмпирическими фактами и научными абстракциями, писал:

"Это старая история. Сперва создают абстракции, отвлекая их от чувственных вещей, а затем желают познавать их чувственно, желают видеть время и обонять пространство. Эмпирик до того втягивается в привычное ему эмпирическое познание, что воображает себя все еще находящимся в области чувственного познания даже тогда, когда он оперирует абстракциями. Мы знаем, что такое час, метр, но не знаем, что такое время и пространство! (Здесь Энгельс повторяет высказывание Негели, снабжая его восклицательным знаком.- П. К.) Как будто время есть что-то иное, нежели совокупность часов, а пространство что-то иное, нежели совокупность кубических метров! Разумеется, обе эти формы существования материи без материи суть ничто, пустые представления, абстракции, существующие только в нашей голове"^*.

^* (Ф. Энгельс, Диалектика природы, Госполитиздат, 1955, стр. 187.)

Через тридцать лет после того, как Энгельсом были написаны эти строки, Эйнштейн показал, что ньютоновское пространство и время, оторванные от материи, это действительно пустые абстракции, с которыми физику делать нечего. Эйнштейн указывает физические способы определения пространства и времени, опираясь на следующие два постулата:

1. скорость света во всех инерциальных системах отсчета одинакова;
2. (принцип относительности): все инерциальные системы одинаково подходят для описания любых физических процессов.

Эти постулаты Эйнштейна представляют, таким образом, обобщение и развитие принципа относительности Галилея-Гюйгенса-Ньютона. Однако сама механика Галилея-Гюйгенса-Ньютона претерпевает при этом существенные изменения. Во-первых, понятие одновременности теряет свой абсолютный смысл: события, одновременные в одной системе отсчета, оказываются разновременными в другой; во-вторых, теряют абсолютный смысл масштабы пространства и времени, пространственный масштаб имеет наибольшую длину в той системе, в которой он покоится, и укорачивается во всех других системах; интервал времени имеет наименьшее значение при его отсчете по часам, покоящимся в данной системе, и растягивается для всех других систем. Формулами преобразования в теории относительности являются преобразования Лорентца. Из этих преобразований вытекает закон сложения скоростей, обеспечивающий правильный результат как опыта Физо, так и опыта Майкельсона. Требование инвариантности фазы световой волны для всех инерциальных систем дает эффект Допплера и аберрацию, причем в отличие от классической теории изменение частоты зависит только от относительной скорости источника и наблюдателя, скорость по отношению к "эфиру" теряет смысл. Кроме того, теория дает так называемый "поперечный" эффект Допплера, представляющий не что иное, как "запаздывание" движущихся часов, в роли которых выступает любой периодический процесс.

Дальнейшими следствиями теории является закон зависимости массы от скорости и тесно связанный с ним знаменитый закон эквивалентности массы и энергии, точнее говоря, закон пропорциональности массы и энергии (Е = mс²).

В 1908 г. учитель Эйнштейна Герман Минковский (1864-1909) сделал доклад "Пространство и время", в котором чисто формальным приемом включения в качестве четвертой координаты величины х₄ = ict дал геометрическую интерпретацию преобразований Лорентца и теории относительности. Согласно этой интерпретации, законы природы должны быть сформулированы на языке четырехмерного векторного и тензорного анализа, что обеспечивает их абсолютный характер, не зависящий от выбора системы отсчета. Геометрическая формулировка Минковского представляла первый шаг в отходе физики от усвоенного ею эвклидова пространства. Геометрия Эйнштейна-Минковского - это четырехмерная "псевдо-эвклидова" геометрия. При дальнейшем обобщении своей теории Эйнштейн перешел к неэвклидовой геометрии, в то время как до этого эвклидова геометрия считалась единственно возможной для формулировки пространственных соотношений в физике. В частности, с эвклидовостью пространства теснейшим образом связан закон инерции. Аксиомы и постулаты эвклидовой геометрии казались настолько "очевидными", что Кант считал их врожденными идеями человеческого сознания. Но среди постулатов Эвклида был один так называемый пятый постулат о параллельных, не обладавший такой очевидностью, и геометры потратили немало труда на его доказательство. Однако эти доказательства или основывались на ошибках, или взамен пятого постулата выдвигали другую гипотезу. С точки зрения физики интересна идея подобия, выдвигаемая Карно и Лапласом. У Лапласа связь эвклидовой геометрии с механикой Ньютона ощущается весьма ясно. Закон тяготения Ньютона представляет собой строго доказанный закон природы. Но из этого закона вытекает в дальнейшем закон подобия: при пропорциональном уменьшении размеров тел, их взаимных расстояний и скоростей тела будут описывать подобные орбиты (см. раздел о Ньютоне). В связи с этим Лаплас пишет: "Попытки геометров доказать постулат Эвклида о параллельных линиях до сих пор оставались безуспешными. Но в то же время никто не подвергает сомнению ни этот постулат, ни теоремы, выводимые из него Эвклидом. Таким образом, восприятие пространства заключает в себе особенное свойство, которое само по себе очевидно и без которого нельзя строго обосновать свойств параллельных линий. Представление об ограниченном протяжении, например о круге, не содержит в себе ничего, что зависело бы от его абсолютной величины. Но если мы мысленно уменьшим его радиус, то непреодолимо должны будем уменьшить в том же отношении его окружность и стороны всех вписанных фигур. Эта пропорциональность представляется мне постулатом, более естественным, нежели эвклидов,и важно то, что с ним мы вновь встречаемся при рассмотрении следствий из всемирного тяготения".

Это, по-видимому, одна из первых попыток апелляции к опыту в обосновании геометрии. Опыт ньютоновской механики явился, таким образом, свидетельством в пользу эвклидовой геометрии, новым доказательством ее "абсолютного" значения. Тем не менее внутренняя неудовлетворенность математиков аксиоматикой Эвклида оставалась. Она привела в первой четверти XIX в. к созданию неэвклидовой геометрии. Первые печатные изложения неэвклидовой геометрии принадлежат гениальному русскому математику профессору Казанского университета Николаю Ивановичу Лобачевскому (1792-1856 гг.).

Николай Иванович Лобачевский

12(24) февраля 1826 г. Лобачевский представляет совету физико-математического факультета Казанского университета "Рассуждение о началах геометрии", в котором излагает принципы геометрии более общего класса, чем эвклидова. В 1829-1830 гг. он напечатал статью "О началах геометрии". В 1835 г. появляются его сочинения "Воображаемая геометрия" и "Новые начала геометрии с полной теорией параллельных". В 1840 г. на немецком языке выходит его сочинение "Геометрические исследования о параллельных прямых", а в 1855 г., за год до смерти,- "Пан-геометрия". Чрезвычайно существенно, что Лобачевский, вопреки кантианским взглядам об априорном происхождении геометрических аксиом, утверждает, что геометрия по своей сущности является опытной наукой. В "Новых началах геометрии" он пишет:

"Всем известно, что в геометрии теория параллельных до сих пор оставалась несовершенной. Напрасное старание со времен Эвклида в продолжение двух тысяч лет заставило меня подозревать, что в самих понятиях еще не заключается той истины, которую хотели доказывать и которую проверить, подобно другим физическим законам, могут лишь опыты, каковы, например, астрономические наблюдения. В справедливости моей догадки будучи, наконец, убежденным и почитая затруднительный вопрос решенным вполне, писал об этом я рассуждение в 1826 году".

Заменив постулат Эвклида постулатом, что через точку вне данной прямой можно провести бесчисленное множество прямых, лежащих внутри некоторого угла параллельности П(а), где а - расстояние точки от данной прямой, не пересекающих эту прямую, Лобачевский строит внутренне непротиворечивую систему геометрии, отличную от эвклидовой. Таким образом, эвклидова геометрия не является единственной логически мыслимой геометрией.

В 1828 г. знаменитый немецкий математик Гаусс разработал аналитический аппарат теории поверхностей. Положение точки на поверхности определяется системой пересекающихся друг с другом двух семейств кривых u и v. На плоскости эти семейства кривых - прямые и определяют декартовы координаты. Каждой точке на поверхности соответствуют два числа u и v, называемые криволинейными координатами. Элемент длины расстояние между двумя соседними точками) выражается формулой:

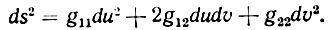
Коэффициенты g_ik Гаусс назвал фундаментальными величинами первого порядка; они характеризуют поверхность независимо от ее положения в пространстве. При изгибании поверхности его элемент длины ("метрика") остается без изменения. Для всех поверхностей, навертывающихся на плоскость без растяжения и сжатия, элемент длины может быть при соответствующем выборе криволинейных координат приведен к виду:

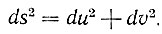
Для всех поверхностей, навертывающихся на шар, элемент длины может быть приведен к виду:

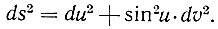
Для так называемой "псевдосферы" и всех поверхностей, навертывающихся на нее,

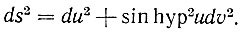
Коэффициенты g_ik и их производные определяют кривизну поверхности. Для плоскости эта кривизна нуль, для сферы ¹/_R, для псевдосферы 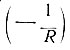. Планиметрия Лобачевского есть планиметрия поверхностей, навертывающихся на псевдосферу. Для плоскости сумма углов треугольника равна двум прямым, для сферы - больше двух прямых, для псевдосферы - меньше двух прямых. Все поверхности, навертывающиеся на одну и ту же поверхность, имеют одну и ту же геометрию. При навертывании их геодезические линии (т. е. линии наименьшей длины) совпадают.

В 1854 г. ученик Гаусса Бернгард Риман (1826-1866) выступил со знаменитой диссертацией "О гипотезах, лежащих в основании геометрии", в которой он обобщил идеи Гаусса и Лобачевского, введя представление о многомерном пространстве. Риман обобщает для этого пространства понятие элемента длины:

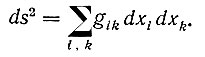
Пространство, для которого этот элемент может быть сведен к сумме квадратов координат (g_ik = 0 для i≠k и 1 для i = k), называется плоским. В противном случае пространство имеет кривизну, определяемую некоторой совокупностью величин, называемых римановым тензором кривизны. Для положительной кривизны получаем риманово беспредельное, но замкнутое пространство n-измерений, которое в частном случае двух измерений сводится к сфере. Для отрицательной кривизны получаем пространство Лобачевского. Следует отметить, что все эти понятия Риман относит к бесконечно малым областям пространства. Кривизна может меняться от точки к точке - составляющие римановы тензора являются функциями точки. Риман ставит вопрос о внутренней причине возникновения метрических свойств пространства. Здесь он делает очень важные и глубокие замечания, что или "то реальное, что создает идею пространства, образует дискретное многообразие, или же нужно пытаться объяснить возникновение метрических отношений чем-то внешним - силами связи, действующими на это реальное".

Еще раньше Лобачевский утверждал, что "силы все производят одно: движение, скорость, время, массу, даже расстояния и углы".

Английский математик Вильям Клиффорд (1845-1879), назвавший Лобачевского Коперником геометрии, спрашивал: "Не окажется ли, что все или некоторые из тех причин, которые мы называем физическими, ведут свое начало от геометрического строения нашего пространства?" Так мало-помалу укреплялась мысль о теснейшей связи пространства и времени с материей, о том, что геометрия является частью физики.

В 1868 г. появилась работа Гельмгольца "О фактах, лежащих в основании геометрии", развивающая идеи Римана. Далее,норвежский математик Софус Л и применил к исследованию пространства созданную им теорию непрерывных групп преобразования. В 1901 г. Риччи создал математический аппарат тензорного исчисления, названный им "абсолютным дифференциальным исчислением", позволяющий формулировать законы природы в форме инвариантной при линейных преобразованиях координат. Эти изменения взглядов на пространство и созданный математиками новый формализм получили применение в общей теории относительности Эйнштейна (1916 г.). В этой теории Эйнштейн, опираясь на известный со времен Галилея факт пропорциональности веса и массы, строит физику поля, справедливую для любых систем отсчета. Геометрия четырехмерного пространства-времени определяется распределением масс. Вместо закона тяготения Ньютона появляются тензорные дифференциальные уравнения. В качестве следствий из общей теории относительности получаются: искривление светового луча в сильном гравитационном поле, движение перигелия Меркурия, смещение спектральных линий в гравитационном поле. По теории Эйнштейна, гравитационное поле неподвижного и вращающегося шара должно быть различным. Этот результат может быть проверен на искусственных спутниках Земли. Что же касается искривления светового луча в гравитационном поле, то наблюдения при полных солнечных затмениях подтвердили теорию в пределах точности эксперимента. Красное смешение спектральных линий в гравитационном поле существует, но полной количественной проверки еще не удалось получить.