Физика возникновения новой науки

Если мы обратимся к рассмотрению конкретных достижений физики эпохи возникновения новой науки (1450-1600), то обнаружим, что основным достижением этой эпохи является освоение античной статики и её завершение. Как было сказано в главе об античной физике, статика древних ещё не решила задачи о наклонной плоскости и равновесии косого рычага (рычага произвольной формы). Эти задачи и были решены в рассматриваемую нами эпоху.

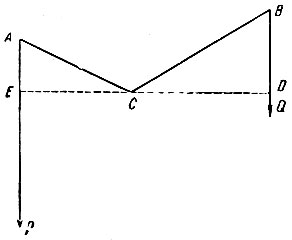
Рис. 52

Леонардо да Винчи сводит задачу косого рычага к прямому. Если на рычаг АСВ (рис. 52) действуют по направлениям АР и BQ грузы Р и Q и рычаг остаётся в равновесии, то в равновесии будет и рычаг ECD, плечи которого перпендикулярны к направлениям действия грузов^*. Закон равновесия прямого рычага известен.

^* (Его Леонардо называет "потенциальным".)

Леонардо не установил закона равновесия тела на наклонной плоскости. Однако, он установил опытным путём, что время ската по наклонной плоскости во столько раз больше времени прямого падения, во сколько раз длина больше высоты. Ему же принадлежит утверждение, что тело скатывается скорее по дуге окружности, чем по стягивающей её хорде.

Освоение античной статики особенно продвинулось со времени Коммандино (1509-1575). Он перевёл трактаты Архимеда, Герона, Паппа, Эвклида, Аполлония и других. По этим переводам учёные средневековья знакомились с наукой древних, осваивали её и развивали дальше. Именно так поступил ученик Коммандино Гвидо-Убальди, маркиз дель-Монте (1545-1607), имя которого встречается в биографии Галилея. Сам Гвидо-Убальди также занимался переводами. Его трактат по механике вышел в 1577 г. В нём он анализирует статику древних и, не зная об исследованиях Леонардо, выводит закон равновесия косого рычага. Лагранж называет дель-Монте основателем принципа возможных перемещений. Во всяком случае, физика ему обязана введением термина "момент" в том виде, в каком он и доныне удержался в статике. Латинское слово "momentum" означает важный, значительный. Чтобы подчеркнуть, что в равновесии рычага важна не только величина сил, но и их перпендикулярные расстояния от оси ("плечо" по современной терминологии), он вводит термин "момент" и формулирует условие равновесия рычага в виде равенства моментов. Исследования Убальди послужили толчком к статическим работам Галилея.

Рис. 53. Титул книги Стевина

Своё завершение статика нашла в работах голландского учёного Стевина (1548-1620), трактат которого "Начала статики" вышел в 1587 г. Правда, его исследования не оказали прямого правда, его исследования не оказали прямого и непосредственного влияния на современную ему науку. Галилей занимался статикой, не зная о работах Стевина. Это объяснялось тем, что Стевин писал свои сочинения на голландском языке. Стевин - уже вполне сложившийся учёный нового типа. К строгости математических рассуждений он прибавляет опытную проверку. Руководящим принципом в его статических работах является принцип невозможности вечного движения. В этом он (хотя и независимо) следует Леонардо, писавшему: "Искатели вечного движения, какое количество пустейших замыслов пустили вы в мир, идите к искателям золота". На титульном листе каждой части трактата Стевина красуется наклонная плоскость, обвитая цепью, с надписью наверху "Чудо и не чудо". Именно таким путём Стевин решил задачу о наклонной плоскости.

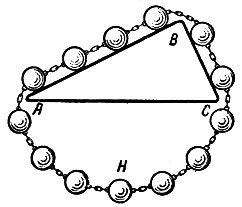
Рис. 54. Наклонная плоскость (по Стевину)

Пусть цепь АВСН обвивает треугольник ABC (рис. 54). Если бы сила, действующая на тело, лежащее на наклонной плоскости, равнялась весу, то обладающая большим весом часть А В скатывалась бы вниз, перетягивая остальные звенья цепи. Но тогда непрерывно поддерживалось бы существующее положение, и цепь, раз начав двигаться, двигалась бы непрерывно, а это, как думает Стевин, невозможно. Отсюда он заключает, что сила, скатывающая тело с наклонной плоскости, не равна весу, а во столько раз его меньше, во сколько высота плоскости меньше её длины. Этот вывод даёт возможность Стевину формулировать закон геометрического сложения сил, и именно отсюда ведёт своё происхождение обозначение сил стрелками. Стевин указывает, что если три силы параллельны и пропорциональны сторонам треугольника, то они уравновешиваются. Вот в каком виде был открыт "параллелограмм сил".

Изучая равновесие полиспастов, Стевин сформулировал, для частного случая, принцип возможных перемещений. Равновесие между грузом, подвешенным на полиспасте, и силой, его поддерживающей, будет достигнуто тогда, когда груз будет во столько раз больше силы, во сколько раз путь, проходимый поднимающей силой при поднятии груза, больше пути, проходимого грузом.

О работах Стевина по гидростатике будет сказано в VII главе в связи с исследованиями Галилея и Паскаля. Укажем только, что Стевин не только восстановил в правах Архимеда, но и развил учение о равновесии жидкостей дальше, открыв всестороннее давление жидкостей и принцип сообщающихся сосудов.

Чтобы довершить характеристику Стевина, упомянем, что им была сконструирована повозка с парусами (буер), движимая ветром, которая, везя 18 человек, пробежала за два часа четыре голландских мили (около семи километров).

Стевин, открыв закон наклонной плоскости и параллелограмм сил, завершил статику. Но, как было уже сказано, его исследования не были известны даже последующим учёным, как например Паскалю. И Галилей например Паскалю. Галилей в полной мере разделяет со Стевиным приоритет в открытии закона равновесия тела на наклонной плоскости. Его доказательство основано на сведении задачи к закону равновесия косого рычага. Мы остановимся здесь только на галилеевом доказательстве закона рычага и его формулировке понятия момента.

Закон рычага Галилей доказывает очень изящно.

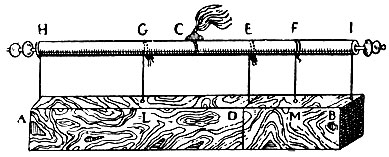
Рис. 55. Рычаг (по Галилею)

Представим, что на невесомой палочке подвешена однородная призма АВ (рис. 55). Призма будет в равновесии, если она закреплена в центре С. Разделим призму на две произвольные части m = AD и n = DB, веса которых Р и Q равны соответственно т и п. Равновесие не нарушается, если каждую из этих частей подвесить соответственно в её середине. Но нетрудно видеть, что G и F - точки приложения весов грузов Р и Q - отстоят от точки опоры С на расстояниях, обратно пропорциональных грузам.

Но уже дель-Монте понимал эквивалентность груза и поднимающей его силы. Механика должна была устранить различие между грузом и усилием и абстрагировать общее понятие "силы". Эта абстракция далась не сразу. Отчётливо понятие силы сформулировано Ньютоном. Галилей, понимая, что для вращательного движения (как в случае рычага) важна не только сила, а и её плечо, и желая дать общее понятие, вводит термин "момент".

"Под именем момента,- говорит он,- в механике разумеется та сила, то усилие, то действие, с которым двигатель двигает и движимое сопротивляется; эта сила зависит не только от простой тяжести, но и от скорости движения и от различного наклона путей, по которым совершается движение, потому что тяжесть производит большее действие при опускании по более наклонному пути, чем по менее наклонному".

В пояснение своего определения, Галилей приводит принцип равновесия не равноплечего рычага, сформулированный им в терминах начала возможных перемещений:

"Неравные по абсолютной величине грузы могут взаимно уравновешиваться и приобретать равные моменты всякий раз, когда их вес будет обратно пропорционален скорости их движения, т. е. когда один груз будет во столько же раз легче другого, во сколько раз скорость его движения будет больше скорости другого".

Мы видим, таким образом, что к концу XVI в. не только была освоена античная статика, но, и более того, она начала превращаться в систематическую отрасль естествознания, стали формулироваться общие определения и принципы, пригодные для решения любой статической задачи.

Таков важнейший итог физики переходного периода.

Но физика этого периода не ограничилась только статикой. Практика уже требовала динамики, и ощупью, неуверенно естествознание делало первые шаги в установлении динамических принципов. Переворот в динамике был совершён Галилеем, но уже его предшественники начали штурм аристотелевской динамики.

Повод к первым механическим изысканиям, несомненно, дала баллистика. Изучение траектории вылетевшего снаряда составило предмет изыскания Тартальи и Кардана.

Николай Тарталья (1501-1559) - один из крупнейших математиков переходной эпохи. Ему принадлежит формула решения кубических уравнений (так наз. "формула Кардана", впервые её опубликовавшего, по сведениям, полученным от Тартальи). Тарталья первым начал распутывать аристотелевское учение о естественных и насильственных движениях. Он смог уже обнаружить несостоятельность воззрений перипатетиков в вопросе о траектории снаряда. Перипатетики учили, что траектория снаряда слагается из насильственного прямолинейного горизонтального пути, смешанного кругового и естественного вертикального. Тарталья нашёл, что вся траектория снаряда криволинейная. Правда, он ещё не решается отрицать полностью учения о естественном и насильственном движении и говорит о непрерывном смешивании обоих движений в процессе полёта снаряда. Любопытно, что эта идея о смешивании естественного и насильственного движений приводит его к правильному выводу о том, что наибольшая дальность полёта будет при угле вылета, равном 45° (равновесие между естественным и насильственным движением).

Современник Тарталья Иероним Кардан (1501-1576) интересен прежде всего своей биографией. Это колоритнейшая фигура эпохи. Он характеризует сам себя в следующих выражениях: "Я обладаю от природы философским и способным к наукам умом. Я остроумен, изящен, приличен, сладострастен, весельчак, благочестив, верен, друг мудрости, мыслящий, предприимчив, любознателен, услужлив, соревнующ, изобретателен, учён своими собственными усилиями, стремлюсь к чудесам, хитёр, ожесточён, сведущ в тайнах науки, трезв, работящ, меланхоличен, коварен, предатель, колдун, маг, несчастный, не любящий своих, склонен к одиночеству, противен, строг, предсказатель, ревнивец, шутник, клеветник, податливый, изменчивый,- вот какие во мне противоречия характера и поведения".

Бурная жизнь этого человека знала нищету и роскошь, путешествия и профессорскую кафедру, тюрьму и дворец. Он перенёс чуму и видел казнь своего сына. Сам отрезал в наказание уши другому своему сыну. Сам предсказал себе смерть на семьдесят пятом году и, как говорят, чтобы исполнить предсказание уморил себя голодом. С именем Кардана в науке связывается, как было уже отмечено, формула Кардана и карданов подвес, имеющий назначением сохранить равновесие тела при любых колебаниях точки опоры.

Кардан производит опыты и критикует физику средневековья: он правильно ставит задачу о равновесии тела на наклонной плоскости, однако не находит верного решения. Короче говоря, в истории науки Кардан характерен, как колоритная фигура эпохи, но существенных результатов в науку он не внёс, хотя и сохранил своё имя в её истории.

Наибольших успехов в деле создания динамики добился Бендетти (1530-1590). Он был первым, учившим, что камень, брошенный горизонтально, движется не насильственно, а в силу сообщённого импульса или, как он говорил, "впечатления". Он утверждал далее, что "тело, вращаемое пращой, по выбрасывании стремится продолжать движение по прямой линии". Наконец, он говорит об одинаковом падении тел в пустоте. Как видим, Бендетти наиболее близко подошёл к открытиям, обессмертившим имя Галилея.

Наряду с механикой развивалась и оптика. Значительный вклад в оптику внёс Леонардо, впервые установивший, что глаз принципиально схож с камер-обскурой. Он же объяснил стереоскопичность зрения видением двумя глазами. Ему же принадлежат первые идеи о волновом движении, и он был первым, наблюдавшим стоячие водяные волны. Попутно укажем, что первое упоминание о капиллярных явлениях принадлежит Леонардо.

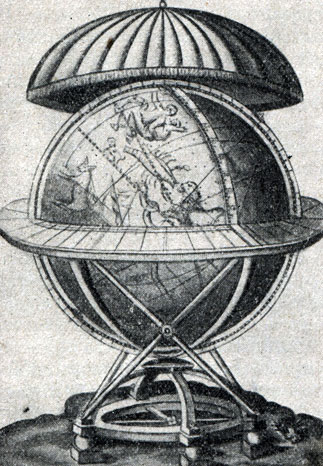
Рис. 56. Небесный глобус 1584 г. (по Тихо Браге.)

Камер-обскура вообще в описываемую эпоху стала распространённым физическим прибором. Принципом камеры Мавролик^* (1494-1575) объяснил круглые пятна на тенистой дорожке. Порта (1538-1615) в своей "Натуральной магии" не только подробно описывает опыты с камер-обскурой, но и указывает, что её действие улучшается применением чечевицы. "Теперь сообщу Вам то, о чём доселе молчал и думал, что должен молчать. Если пометить у отверстия чечевицеобразное стекло, то всё изображение будет отчётливее; увидишь и лица людей проходящих, платья, цвета, движение, всё как будто было вблизи. Зрелище так приятно, что видевшие не могли вдоволь надивиться". Поясним, что камер-обскура Порта была комнатой с окнами, закрытыми ставнями.

^* (Мавролику принадлежит объяснение действия очков, основанное на понимании рэли хрусталика как собирательной линзы. Очки исправляют дефекты фокусирующего действия хрусталика.)

Говоря о Порта, необходимо упомянуть об одном важном обстоятельстве, характерном для периода возникновения новой науки. Порта не удовлетворился собственными изысканиями (правда, часто носившими полусерьёзный характер), а организовал научное общество "Академия тайн природы". Новая наука, выходя из рамок казённой схоластики, ищет новых организационных форм. Университеты - цитадель официальной науки - не могут быть центрами новой науки, организуются научные кружки, общества, так называемые "академии". Таково было общество в Милане, связанное с Леонардо да Винчи, такова была академия Телезия (1508-1588), организованная для борьбы с натурфилософией Аристотеля. Такова была и академия Порта. Церковь преследовала эти ячейки новой мысли в самом зародыше. Академии Телезия и Порта были закрыты. Но уже во второй половине семнадцатого века академии стали прочными научными центрами.

Мы не будем останавливаться на других сторонах развития новой науки. В качестве общего вывода сформулируем:

Новые задачи, вызванные жизнью, породили новое естествознание. В течение полутораста лет (вторая половина пятнадцатого века и шестнадцатый век) происходит процесс формирования новых идей. В напряжённой борьбе с реакционными силами старой идеологии выковывается новое естествознание. Решительное наступление буржуазии, предпринятое в семнадцатом веке, обеспечивает победу новой науки.

Таким образом, семнадцатый век является периодом упрочнения нового мировоззрения и новой науки. Этот период открывается Галилеем и заканчивается Ньютоном.