Теория удара

Проблема удара - это проблема взаимодействия системы тел, и представляется она чрезвычайно сложной. Понятно, что законы удара не могли быть сразу найдены правильно в ту эпоху, когда ещё только формировались понятия динамики точки. Первым занявшимся проблемой удара был Галилей. Его результаты изложены в "Беседах" (Discorsi), в беседе 6-го дня. Галилей не смог решить проблемы, и самая постановка им проблемы отличается от обычной. Его интересует прежде всего вопрос о мере силы удара, об опытных способах измерения этой силы. В этих целях он проделал следующий опыт. На коромысле, вращающемся около неподвижной центральной оси, были уравновешены два груза, один из которых представлял два ведра, подвешенных один над другим на некотором расстоянии друг от друга. В верхнем сосуде имелось в дне отверстие, которое можно было закрывать и открывать, в сосуд наливалась вода. Вся эта система уравновешивалась противовесом. Так как ударяющее тело движется, то оно, по Галилею, должно обладать тем большим моментом, чем больше вес и скорость тела. Ожидалось поэтому, что по открытии задвижки равновесие нарушится, противовес поднимется, и перегрузок, который надо добавить к весу противовеса, может служить мерой удара водяной струи. Однако оказалось, что в начальный момент нарушение равновесия произошло в противоположную сторону (противовес опустился), а затем, когда струя достигла нижнего сосуда, равновесие восстановилось. Этот опыт Галилея является прекрасной иллюстрацией закона сохранения количества движения, но он не дал ему ответа на вопрос о мере удара. В конце концов Галилей приходит к выводу, что сила удара бесконечно велика или во всяком случае неопределённа. Важно отметить, что в своих рассуждениях Галилей весьма четко различает "мёртвую силу", силу давящего груза, и "живую силу"^*, силу движущегося груза. Чтобы произвести такое же действие на сваю, какое производит "баба", падающая с высоты, необходимо значительно превосходящее вес падающей бабы давление "мёртвого" груза. Тем самым Галилей сделал первый шаг в вопросе о законе сохранения энергии и мере движения.

^* (Правда, термина "живая сила" Галилей не употребляет, этот термин введён; позднее Лейбницем.)

Декарт, для которого все взаимодействия тел сводились к давлению и удару, вплотную занялся проблемой удара. Руководящим принципом для него является закон сохранения количества движения. Но Декарт, как уже отмечалось, суммировал количества движения арифметически и нечётко различал упругие тела от неупругих. Поэтому его теория является ошибочной, причём некоторые ошибки настолько грубы, что достаточно элементарного опыта для их опровержения. Вот "правила удара" Декарта, формулированные для твёрдых тел.

1. Два одинаковых тела с равными и противоположными скоростями после удара обмениваются скоростями.
2. Если одно тело В хоть несколько больше другого тела С, то после удара оба тела движутся по направлению В с одинаковыми скоростями.
3. Если В и С равны по величине, по у В большая скорость, то В отдаёт С половину излишка, скорости.
4. Если С>В (хотя бы немного) и покоится, то В отскакивает от него с противоположной скоростью.
5. Если С<В и покоится, то оба тела будут двигаться с одинаковой скоростью, причём В отдаёт соответственно массам часть своей скорости С.
6. Если В и С равны, то С движется в направлении В, а В отскакивает.
7. Седьмым правилом регламентируется распределение скоростей при одинаковом направлении скоростей соударяющихся тел.

Декарт видел несоответствие своих правил с данными опыта, но считал, что поскольку идеально твёрдых тел в природе нет, то и не может быть полного соответствия его теории с опытом.

С большим успехом занимался проблемой удара Иоганн Марци (1595-1667), выпустивший в 1639 г. трактат "De proportione motus seu regula sphymica". Марци разделяет тела на мягкие, хрупкие и твёрдые и для последних (упругих) дал следующие законы:

1. Если движущееся тело соударяется с равным ему покоящимся, то оно останавливается, а покоящееся тело получает скорость движущегося.
2. Два равных тела, соударяющихся с равными и противоположными скоростями, после удара обмениваются скоростями.

Проблема удара, в её крайних случаях (упругий и неупругий центральные удары), была решена в связи с конкурсом, объявленным в 1668 г. Королевским обществом в Лондоне. Правда, Гюйгенс теоретически, а Рен экспериментально занимались этой проблемой и до конкурса. На конкурс были представлены результаты математика Валлиса (1616-1703), давшего теорию неупругого удара, архитектора Рена (1632-1722) и знаменитого физика и математика Гюйгенса. Рен и Гюйгенс разобрали упругий удар. Все исследователи установили закон сохранения количества движения в алгебраической форме (поскольку скорости соударяющихся тел направлены по одной прямой), но Гюйгенс нашёл, кроме того, что при упругом ударе сохраняется сумма произведений масс на квадраты скоростей соударяющихся тел. Доказательства результатов Гюйгенса были опубликованы уже после его смерти в 1703 г. Опытной проверкой законов удара занимались Рен и Мариотт, подтвердившие закон сохранения количества движения. Но только Ньютон связал этот закон с третьим принципом механики и довёл до конца работу по обоснованию механики.

Гюйгенсовская теория упругого удара замечательна её связью с принципом относительности. Основными положениями его теории являются:

1. закон инерции,
2. постулат об обмене скоростями соударяющихся упругих (твёрдых по терминологии Гюйгенса) тел, обладающих равными массами и противоположными скоростями, и
3. постулат, утверждающий, что скорость равномерного и прямолинейного движения системы, в которой рассматривается удар, не влияет на процесс соударения (принцип относительности в применении к явлению удара).

"Так, например,- поясняет Гюйгенс этот постулат,- когда пассажир некоторого корабля, движущегося с постоянной скоростью, приводит к соударению два равных шара с равными по отношению к нему и частям корабля скоростями, то они должны отскочить с равными же, по отношению к нему, скоростями, точно так же, как это имеет место для стоящего на берегу и соударяющего те же шары с равными скоростями".

Гюйгенс, пользуясь принципом Галилея, как эвристическим принципом, находит законы упругого удара. Чтобы дать представление о методе Гюйгенса, приведём доказательство первой теоремы его теории.

Теорема 1.

"Если о покоящееся тело ударяет другое равное тело, то это другое тело будет после удара покоиться, а покоящееся получит ту же самую скорость, какой обладало ударяющее.

Представим себе, что бот увлекается потоком вдоль берега и так близко к берегу, что стоящий на нем пассажир может протянуть руки стоящему на берегу спутнику. Едущий может держать в своих руках А и В два равных, подвешенных на нитях тела Е и F, расстояние EF между ними в точке G делится пополам (рис. 77). Равным встречным движением рук относительно себя и лодки он приводит к соударению шары Е и F также с одинаковыми скоростями, и они должны (постулат 2) отскочить после удара также с одинаковыми скоростями (относительного его и бота).

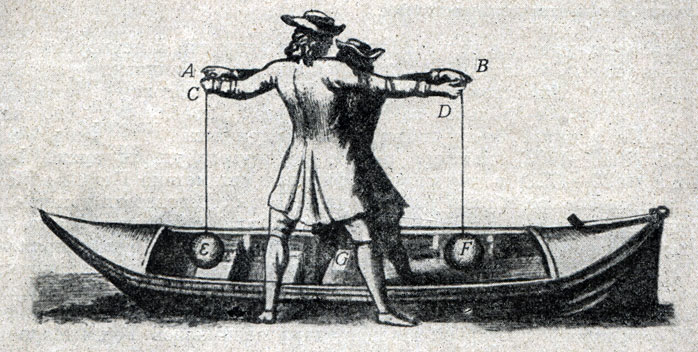
Рис. 77

Однако судно мыслится увлекаемым в левую сторону со скоростью GE, т. е. с такой же скоростью, с какой рука А двигалась вправо. Поэтому очевидно, что рука А для спутника на берегу остаётся неподвижной, а рука В, с точки зрения того же спутника, движется со скоростью FE, равной двойной скорости GE и FG.

Таким образом, если представить себе, что спутник на берегу схватывает своей рукой С руку А едущего и вместе с тем конец нити, несущей шар Е, а другой рукой D руку В едущего, несущую нить, на которой висит шар F, то ясно, что в то время как пассажир сближает шары Е и F с равными скоростями (по отношению к себе и боту), спутник на земле ударяет о покоящийся шар Е шаром F, движущимся со скоростью FE (по отношению к себе и берегу). Естественно, что для едущего, который движет шары свои связанным образом, ничего не значит, что спутник на берегу схватил его руки и концы нитей, так как он только принимает участие в их движении и не делает им никакого возмущения. По тем же основаниям совершенно не препятствует и спутнику на берегу, приводящему шар F к неподвижному шару Е, что пассажир держит с ним руки, поскольку руки А и С по отношению к берегу покоятся, а руки D и В движутся с той же скоростью FE. Но поскольку, как сказано, шары Е и F после взаимного соприкосновения отскакивают с равными скоростями относительно пассажира и бота и именно шар Е со скоростью GE и шар F со скоростью GF и поскольку в то же время бот увлекается налево со скоростью GE или FG, то по отношению к берегу и неподвижному спутнику выйдет, что шар F после удара останется неподвижным, а другой шар, с той же точки зрения, движется налево с двойной скоростью GE, т. е. с той же скоростью FE, с какой шар F ударился о Е. Мы доказали, таким образом, по отношению к стоящему на земле и ударяющему подвижным телом о неподвижное, что это подвижное тело теряет всё своё движение, а то (неподвижное тело) всё получает, что требовалось доказать"^*.

^* (Поясним рассуждения Гюйгенса простым расчётом.

Пусть в подвижной системе отсчёта К' (бот) скорости шаров Е и F равны соответственно: v₁ = - U, v₂ = + U, где U - скорость системы (бота). Тогда в неподвижной системе К (берег) эти скорости будут:

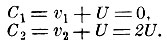
После удара скорости в К' будут (постулат 2):

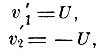
а в К

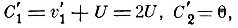
что и доказывает теорему.)

Одним из важнейших результатов гюйгенсовской теории было установление им принципа сохранения живых сил для упругого удара.

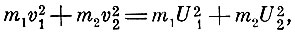
где m₁ и m₂ - массы, а v₁, v₂, U₁ и U₂ - скорости соударяющихся тел.

Это же положение играет фундаментальную роль в его теории физического маятника.

Установлением законов удара завершилась подготовительная стадия работы по обоснованию механики. Все эти принципы были в том или ином виде сформулированы. Оставалось обобщить их в единую систему, что и было сделано Ньютоном.