Гидростатика и гидродинамика

Существенные результаты были получены и в механике сплошных сред. Трактаты Стевина, Галилея и" Паскаля заложили основы гидростатики, восстановив в правах Архимеда и дав новое обоснование его знаменитому закону. Стевин в своих "Принципах равновесия" (1586) доказывает закон Архимеда, опираясь на принцип отвердевания. Представим себе жидкость в сосуде, находящуюся в равновесии. Очевидно, что равновесие не будет нарушено, если часть жидких частиц утратит свою подвижность и некоторый объём внутри жидкости приобретёт свойства твёрдого тела. Так как этот объём находится в равновесии, то очевидно, что вес его уравновешивается равнодействующей сил давлений со стороны, окружающей выделенный объём жидкости. Таким образом, на тело, погружённое в жидкость, действует сила, направленная вертикально снизу вверх и равная весу жидкости в объёме тела.

Паскаль

В том же сочинении Стевин доказывает экспериментально и теоретически гидростатический парадокс - независимость весового давления от формы сосуда - и вычисляет давление на боковую стенку (рис. 83, 84). Все эти расчёты нужны ему для выяснения условий плавания тел, в первую очередь кораблей. Стевин писал свои работы на голландском языке, поэтому вполне понятно, что они остались неизвестными Галилею и Паскалю. Галилей в своём "Рассуждении о телах, пребывающих в воде", опровергая мнение перипатетиков о зависимости плавания от формы тел, восстанавливает закон Архимеда. Чрезвычайно существенно, что своё доказательство Галилей обосновывает принципом виртуальных перемещений. Возражение перипатетиков, что всякая плоская пластина должна плавать, Галилей опровергает опытом, согласно которому плоская пластина большего удельного веса, чем вода, не всплывает. В погружении или плавании тел играет роль плотность. Так, восковой шарик тонет в воде, но если к ней подбавить соли, то при надлежащей концентрации он всплывает. Интересно отметить, что, признавая факт плавания плоских тяжёлых пластин, Галилей указал, что такие пластины плавают в углублении поверхностной плёнки. Точно так же Галилею известен факт образования капель на капустных листьях и растекание их при смачивании красным вином. От испытующего взора великого учёного не ускользнули, таким образом, и явления, связанные с поверхностным натяжением жидкостей. Его ученики в Флорентийской академии (в особенности Борелли) вплотную приступили к изучению явлений капиллярности. Но время для объяснения этих явлений ещё не настало.

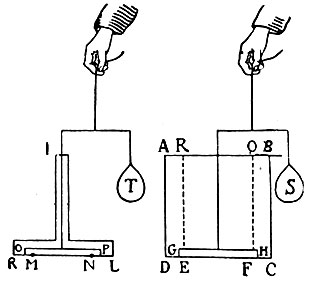
Рис. 83. и 84. К доказательству Стевином гидростатического парадокса

Паскаль в своём трактате о равновесии жидкостей разбирает вопрос наиболее исчерпывающим образом: закон всесторонней передачи давлении в жидкости (закон Паскаля), вычисление весового давления и гидростатический парадокс, закон сообщающихся сосудов и принцип гидростатического пресса - всё это он выводит, широко применяя принцип возможных перемещений. Классические исследования Паскаля о равновесии жидкостей перешли почти без изменения в школьные учебники, вместе с его результатами в изучении атмосферного давления, о которых будет сказано ниже.

Гидродинамика ещё не могла получить столь широкого развития, как гидростатика. Зачатки её мы находим у учеников Галилея - Кастелли и Торичелли. Кастелли в 1628 г., разбирая вопрос о движении жидкости в каналах, установил закон обратной пропорциональности величины скорости движения жидкости площади сечения

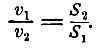
Торичелли, ученик Кастелли, глубоко воспринял идеи Галилея о законах движения и в своём трактате "О движении и о тяжести" (1641) применил динамику Галилея к явлению истечения жидкости из отверстия. Он показал, что скорость вытекания струи равна скорости её падения с высоты уровня в сосуде.

Торичелли

Форма струи, вытекающей из бокового отверстия, должна быть параболической. Трактат Торичелли стал известен Галилею, и Кастелли пред ставил знаменитому учёному молодого Торичелли. Последний год жизни Галилея Торичелли провёл с ним в качестве ученика и преемника.