Маятник

При решении этих важных принципиальных задач большую роль сыграло исследование одной частной проблемы, проблемы маятника. Помимо её исключительного практического значения (часы), она в сильной степени способствовала уяснению принципов динамики и была одной из первых задач динамики системы. Эта задача прошла в XVII в. следующие стадии.

Прежде всего Галилей. Он открывает закон изохронности колебаний маятника при малых амплитудах и устанавливает пропорциональность периода маятника квадрату его длины.

Затем в" 1646 г. "человек-журнал" Мерсенн ставит задачу: найти форму тяжёлого подвешенного тела, которое совершало бы колебания одинаковой продолжительности с математическим маятником заданной длины. Если рассматривать тело, как совокупность маятников различных длин и, следовательно, колеблющихся с разными периодами, то сила связи между ними должна привести к выравниванию этих времён качания. Таким путём Декарт приходит к выводу, что в маятнике должен существовать некоторый центр качания, относительно которого выравниваются периоды качания так, что если бы вся масса тела была сосредоточена в этом центре, то получился бы математический маятник с периодом, равным заданному. Таким образом, все тела, имеющие центры качаний на одинаковых расстояниях от осей, будут качаться с одинаковыми периодами. Тем самым Декарт свёл задачу вычисления периода физического маятника к задаче нахождения центра качаний и решил эту задачу для плоских фигур с осью, лежащей в плоскости фигуры. Роберваль решил задачу для некоторых плоских фигур с осью вращения, перпендикулярной плоскости фигуры. Полное решение задачи было дано Христианом Гюйгенсом в знаменитом сочинении "Horologium oscillatorum", вышедшем в 1673 г. Это небольшое по объёму сочинение, заключавшее теорию кругового движения циклоидального маятника, физического маятника, составило эпоху в развитии механики, подготовив почву для работ Ньютона.

Теоретические изыскания Гюйгенса были тесно увязаны с практической задачей конструкции точных часов. Маятник был надёжным средством, обеспечивающим равномерность их хода. Найденная им конструкция маятниковых часов была запатентована 16 июня 1657 г. и описана в сочинении "Horologium", вышедшем в 1658 г. Продолжая работать над улучшением конструкции часов, он осуществил в 1674 г. проект пружинных часов. Показательно, как свидетельство актуальности проблемы, что вокруг изобретений Гюйгенса разгорелся спор о приоритете. После публикации Гюйгенса ученик Галилея Вивиани опубликовал найденный им в бумагах Галилея проект последнего часов с маятником. В качестве соперника Гюйгенса называли также имя часовщика Поста Бюрги, умершего в 1632 г., а приоритет в изобретении пружинных часов оспаривал неутомимый Гук.

В теоретическом обосновании своих практических изобретений Гюйгенс отправлялся от работ Галилея. Во второй части своих "Маятниковых часов", в предложении восьмом, Гюйгенс доказывает, что движение по кривой линии можно рассматривать как движение по неограниченно большому числу наклонных плоскостей, связывая тем самым задачу криволинейного движения с исследованным Галилеем движением по наклонной плоскости. Следуя Галилею, Гюйгенс доказывает теорему 9: "Падение с равных высот до одного и того же уровня приводит к одинаковым конечным скоростям независимо от формы пути. Справедливо и обратное утверждение, что тело, упавшее с какой-либо высоты, поднимается за счёт полученное скорости до первоначального уровня" (предложение 10). Всё это даёт возможность ввести в динамику новый энергетический принцип, что общий центр тяжести около горизонтальной оси поднимется до первоначальной своей высоты и ни в коем случае не выше. Отправляясь от этого принципа, Гюйгенс строит теорию физического маятника.

Рис. 81. Карманные часы, называемые 'Нюрнбергское яйцо', в начале XVI столетия

Результат, полученный Гюйгенсом для приведённой длины физического маятника, позволяет применить к вычислению его периода закон простого маятника, установленный также Гюйгенсом. В предложении 21 Гюйгенс утверждает, что падение по ряду наклонных плоскостей, содержащихся между одинаковыми горизонталями, совершается тем быстрее, чем больше наклонена плоскость (чем короче её длина).

Обобщая этот результат, известный ещё Галилею, Гюйгенс приходит к основному предложению 25: "Падение и восхождение по циклоиде требует времени, относящегося к времени вертикального падения по её оси, как окружность круга относится к диаметру, и высота начальной точки не изменяет этого времени (таутохронность циклоид)". Построив круг, соприкасающийся с циклоидой в нижней её точке, Гюйгенс доказывает предложение 26: "Время одного малого колебания кругового маятника относится к времени падения по двойной длине маятника, как окружность круга относится к диаметру".

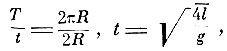
откуда

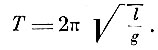
Гюйгенс сейчас же указал на важное приложение полученного результата: измерение длины временем, предложив принять ¹/₃ длины секундного маятника за эталон длины - нормальный фут. Ему же принадлежит идея об измерении ускорения длиной секундного маятника.

Гюйгенс устанавливает далее, что изохронность колебаний кругового маятника является приближённым и что действительно изохронным маятником является циклоидальный. Найдя, что развёртка циклоиды является также циклоидой, Гюйгенс предлагает следующую конструкцию изохронного маятника для часов. Маятник подвешивается на нитке, к обеим сторонам которой прилегают циклоидальные металлические полосы. Тогда его чечевица будет двигаться по циклоиде.

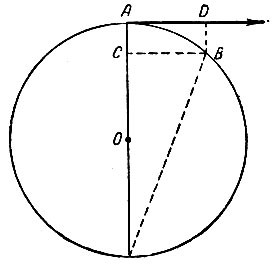
Рис. 82. Вывод величины центростремительного ускорения по Гюйгенсу

Наконец, в том же сочинении Гюйгенс, как было упомянуто выше, даёт закон центростремительного ускорения. Действие центростремительной силы он определяет расстояниями касательной от окружности, характеризующими уклонение движущейся точки от прямолинейного пути по инерции. Нетрудно показать, что уклонение δ = АС (рис. 82) будет пропорционально квадрату скорости и обратно пропорционально радиусу. В самом деле, отрезок касательной AD, проходимый в инерционном движении за малый промежуток времени τ, пропорционален этому промежутку, а уклонение δ = АС = DB, проходимое ускоренным движением, пропорционально τ²:

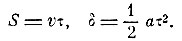
Так как

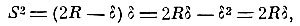
то

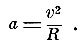
Дадим биографическую справку.

Гюйгенс

Христиан Гюйгенс - сын богатого голландского дворянина, секретаря принца Оранского Константина. Гюйгенс родился 14 апреля 1629 г. Образованный и одарённый отец преподал ему начала математики и механики, но предполагал подготовить сына к юридической деятельности, и в шестнадцатилетнем возрасте Гюйгенс поступает в Лейденский университет изучать право. Однако здесь он предаётся почти целиком математике, механике и астрономии. В нём соединяются блестящие математические дарования с прекрасными практическими навыками. Вместе с братом Константином он шлифует оптические стёкла и с усовершенствованной трубой находит спутника и кольца Сатурна. Мы уже упоминали в тексте о его работе над часами.

В числе разнообразных математических результатов Гюйгенса упомянем о разработке им задач теории вероятностей.

В 1663 г. Гюйгенс был избран членом Лондонского королевского общества, а в 1666 г. членом только что организованной Парижской академии и жил в Париже до 1681 г., когда отмена Нантского эдикта заставила его вернуться на родину. При его деятельном участии Олаф Рёмер производит в Парижской обсерватории наблюдения над спутниками Юпитера, завершившиеся измерением скорости света.

На родине Гюйгенс занимается шлифовкой стёкол, оптическими и космогоническими проблемами. Умер он 8 июня 1695 г.

Итог развития механики в XVII в. до Ньютона таков: были установлены принципы динамики, решены основные задачи теории удара, подготовлена почва для открытия закона тяготения. Все эти спорадические результаты надлежало обобщить и завершить созданием классической механики, что и было выполнено Ньютоном.