Метод флюксий

Сущность этого последнего излагается Ньютоном (в введении к трактату "О квадратуре кривых", изданному в 1704 г.) следующим образом:

"Я рассматриваю здесь математические количества не как состоящие из очень малых постоянных частей, а как производимые непрерывным движением^*. Линии описываются и по мере описания образуются не приложением частей, а непрерывным движением точек, поверхности - движением линий, объёмы - движением поверхностей, углы - вращением сторон, времена - непрерывным течением и т. д.

^* (Курсив всюду мой.- П. К. Непрерывно текущая переменная величина и есть флюента Ньютона. Ньютон отчётливо устанавливает связь своего математического метода с изучением движения.)

Такое происхождение имеет место и на самом деле в природе вещей и наблюдается ежедневно при движении тел. Подобным образом древние объясняли происхождение прямоугольников, ведя подвижные прямые линии по неподвижным.

Замечая, что нарастающие количества, образующиеся по мере нарастания в равные времена, сообразно большей или меньшей скорости их нарастания, оказываются большими или меньшими, я изыскивал способы определения самих количеств по той скорости движения или нарастания, с которой они образуются"^*.

^* (Т. е. нахождения функций по их производным. Это и есть центральная идея метода флюксий, которую Ньютон в письме к Лейбницу дал в зашифрованном виде: 6а, 2с, d, ае, 13е, 2f, 7i, 3l, 9n, 4o, 4q, 1r, 4s, 9t, 12v, х.

Ньютон в первых двух изданиях "Начал" сообщает об этом обмене письмами с Лейбницем: "В письмах, которыми около десяти лет тому назад я обменивался с весьма искусным математиком Лейбницем, я ему сообщал, что я обладаю методом для определения максимумов и минимумов, проведения* касательных и решения тому подобных вопросов, одинаково приложимого как для членов рациональных, так и для иррациональных, причём я её сообщил, переставив буквы следующего предложения: data aequatione quotcumfue fluentes quantiates involventa fluxiones invenire et vice versa (когда задано уравнение, содержащее любое число переменных количеств, найти флюксии, и наоборот). Знаменитейший муж отвечал мне, что он также напал на такую методу, и сообщил мне свою методу, которая оказалась едва отличающейся от моей, и то только терминами и начертанием формул". Отсюда видно, насколько была подготовлена почва для создания новых математических методов.)

"Назвав скорости этих движений или нарастаний флюксиями, образуемые же количества флюентами, я постепенно пришёл около 1665 и 1666 гг. к методу флюксий, который я прилагаю здесь к квадратуре кривых.

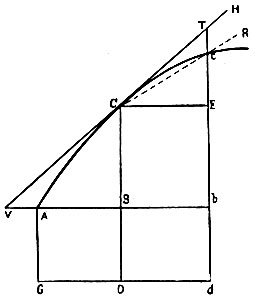
Рис. 108. К методу флюксий

Флюксии приблизительно пропорциональны приращениям флюент, образующимся в равные весьма малые промежутки времени, или, точнее говоря, находятся в предельном отношении зарождающихся приращений и могут быть представлены какими угодно линиями, этим приращениям пропорциональными. Так, если площади ABC, ABDG (рис. 108) описываются ординатами ВС и BD, движущимися равномерно по основанию Аb, то флюксии этих площадей относятся друг к другу, как описывающие ординаты BCnBD, и могут, быть представлены этими ординатами, ибо зарождающиеся приращения площадей пропорциональны этим ординатам.

Пусть ордината ВС из своего положения ВС перешла в какое-нибудь положение bc. Дополнив параллелограмм ВСЕb, проводим прямую VTH, касающуюся кривой в точке С и пересекающую продолжение В А и bc в V и Т; тогда приращения абсциссы АВ, ординаты ВС и длины дуги кривой АС, при этом образовавшиеся, суть Вb, Ес, Сс; стороны треугольника ЕСТ находятся в предельном (первом) отношении этих зарождающихся приращений, следовательно, флюксии самих АВ, ВС и АС пропорциональны сторонам СЕ, ЕТ и ТС треугольника СЕТ, которыми они и могут быть представлены, или, что то же самое,- сторонами треугольника VBC, ему подобного.

То же самое получится, если принять флюксии в предельном (последнем) отношении исчезающих частей. Проведём прямую Сс и продолжим её до R; когда ордината be будет возвращаться к своему первоначальному положению ВС и когда точки с и С сольются, то прямая CR совпадёт с касательной СН, и исчезающий треугольник СЕс в предельном (последнем) своём виде станет подобным треугольнику СЕТ, и его исчезающие стороны будут в пределе относиться друг к другу, как стороны СЕ, ЕТ, ТС треугольника СЕТ, следовательно, в том же отношении находятся и флюксии линий АВ, ВС и АС. Если же точки Сие находятся в каком-нибудь малом удалении друг от друга, то и прямая CR будет находиться в некотором небольшом удалении от касательной. Чтобы прямая CR совпадала с касательной СН и чтобы получились предельные (последние) отношения линий СЕ, Еc и сС, точки С и c должны сойтись и совпасть вполне. В математических вопросах нельзя пренебрегать даже самыми малыми погрешностями.

На основании подобного же рассуждения, если равномерно продвигать круг, описанный из точки В, как центра, радиусом ВС, так, чтобы он оставался перпендикулярным к АВ, то флюксия образуемого объёма ABC будет пропорциональна площади производящего круга, и флюксия образуемой поверхности пропорциональна окружности производящего круга и флюксии длины дуги кривой АС (т. е. их произведению). Ибо в то время как объём образуется, ведя круг по абсциссе АВ, сказанная поверхность образуется, ведя окружность этого круга по длине кривой АС.

Вот ещё три примера этого способа:

I. Прямая РВ вращается около заданного полюса Р и пересекает другую заданную по положению прямую АВ; требуется: найти отношения флюксий прямых АВ и РВ.

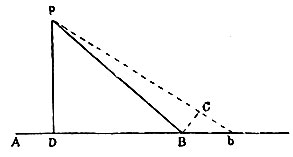
Рис. 109. К методу флюксий

Пусть прямая РВ (рис. 109) перешла из своего положения РВ в новое положение Рb. Отложив по Рb длину, равную РВ, проводим к АВ прямую PD под таким углом bPD, который равен углу bВС. По подобию треугольников bВС и bPD приращение Вb так относится к приращению Сb, как Рb относится к Db. Когда прямая Рb будет возвращена в своё первоначальное положение, чтобы приращения исчезли, то предельное (последнее) отношение приращений, или, что то же, предельное отношение Рb к Db обратится в отношение РВ к BD, причём угол PDB станет прямым, следовательно, и флюксия АВ будет относиться к Флюксии РВ, как РВ к DB.

II. Прямая РВ, вращающаяся около заданного полюса Р, пересекает две другие прямые АВ и АЕ, заданные по положению в точках В и Е; требуется найти отношение флюксий этих прямых.

Когда вращающаяся прямая РВ (рис. 110) переместится из своего положения РВ в положение РЪ, пересекающее заданные прямые АВ и АЕ в точках b и е, то, проведя прямую Вс, параллельную АЕ и пересекающую Рb в с, получим:

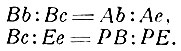
Из этих пропорций следует:

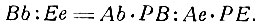
Когда прямая Рb возвратится в первоначальное своё положение РВ, то исчезающее приращение Вb так будет относиться к исчезающему приращению Ее, как АВ*РВ относится к АЕ*РЕ, следовательно, в этом же отношении будет находиться и флюксия прямой АВ к флюксии прямой АЕ.

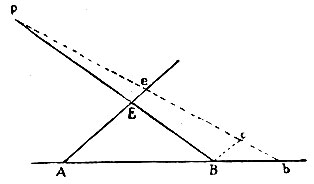
Рис. 110. К методу флюксий

Поэтому, если вращающаяся прямая РВ пересекает какие-либо заданные по положению кривые в точке В и Е и ставшие теперь подвижными прямые АВ и АЕ касаются этих кривых в точках пересечения В и Е, то флюксия длины дуги, кривой, касающейся прямой АВ, будет так относиться к флюксии длины дуги кривой, касающейся прямой АЕ, как АВ РВ относится к АЕРЕ. То же самое получится даже и в том случае, когда прямая РВ будет постоянно касаться до какой-либо заданной по положению кривой в подвижной точке Р.

III. Количество х течёт равномерно, надо найти флюксию количества хⁿ.

В то время как количество х при своём течении обратится в х + h, количество хⁿ обратится в (х + h)ⁿ, т. е. по нашему способу разложения в бесконечные ряды обратится в

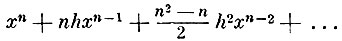
приращения h и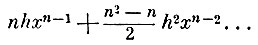

относятся друг к другу, как 1 к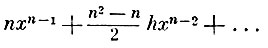

Когда эти приращения исчезнут, то их предельное отношение будет равно отношению 1 к nx^n-1 поэтому флюксия х так относится к флюксии хⁿ, как 1 к nх^n-1.

Рассуждая подобным же образом и пользуясь способом предельных первых и последних отношений, можно составить флюксии прямых или кривых линий в любых случаях, а также и флюксии поверхностей, углов и других количеств. Вместе с тем такое установление этого анализа над количествами конечными и исследование предельных первых и последних отношений, зарождающихся или исчезающих конечных величин, согласно с геометриею древних, и я хотел показать, что в методе флюксий нет надобности вводить в геометрию бесконечно малые фигуры.

Анализ может вестись над какими угодно фигурами, конечными или бесконечно-малыми, которые предполагаются подобными исчезающим фигурам, а также и над фигурами, которые в способе неделимых принимаются за бесконечно-малые; надо лишь поступать с должною осмотрительностью.

Нахождение флюент по их флюксиям - задача более трудная, и первая ступень в её решении равносильна квадратуре кривых, о которой мною уже давно написано следующее сочинение"^*.

^* (Выдержки из Ньютона в тексте приводятся по переводу академика А. Н. Крылова. "Математические начала натуральной философии". Сочинения А. Н. Крылова, т. VII, и академика С. И. Вавилова "Оптика", Гиз, 1927.)

Из приведённого отрывка видно, насколько владели Ньютоном образы непрерывного движения при создании им математического анализа. Равномерно текущая независимая переменная у него, как правило,- время. Флюенты - это переменные величины (например путь), меняющиеся в зависимости от времени. Флюксии - скорости изменения этих величин.

Техника интегрирования у Ньютона основана на развёртывании выражений в бесконечные ряды по аналогии с разложением обыкновенных дробей в десятичные. Последнее стало известным в XVII в., и сам Ньютон называет его "недавно открытым". Поэтому у Ньютона исходной формулой интегрирования и является формула интегрирования степени. Он обобщает эту формулу на случай дробного рационального показателя.

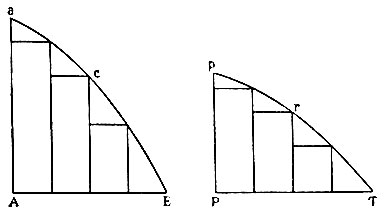
Рис. 111. Площадь криволинейной фигуры

В своём методе флюксий Ньютон создал математический аппарат новой физики. Однако в своём основном труде ("Математические начала натуральной философии") он избегает аналитического метода и прибегает к геометрическим доказательствам, широко используя метод пределов. Вся первая книга "Начал" и посвящена изложению этого метода. Ньютен опирается на лемму, утверждающую равенство пределов двух переменных величин, разность между которыми становится в процессе изменения бесконечно малой. Отсюда он заключает, что пределы сумм площадей, вписанных в криволинейную фигуру АасЕ (рис. 111) прямоугольников и описанных около той же фигуры прямоугольников, совпадают и равны площади этой фигуры. Точно так же из равенства пределов отношений площадей, вписанных в две фигуры прямоугольников, вытекает, что сами площади этих фигур находятся в том же предельном отношении. Отсюда вытекает пропорциональность площадей этих фигур квадратам сторон.

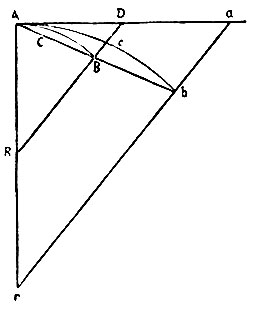
Рис. 112. Предел дуги

Далее Ньютон показывает, что предельное отношение дуги, хорды и касательной к кривой с непрерывно меняющейся кривизной равно единице. Единице равно и предельное отношение площадей треугольников RAB и RAD (рис. 112). Наконец, Ньютон доказывает чрезвычайно существенную для механических приложений лемму IX.

"Если заданные пи положению прямая АЕ и кривая ABC пересекаются под данным углом А и от прямой АЕ проводятся внутри этого угла ординаты BD, СЕ, пересекающие кривую в точках В и С,и точки В и С совместно приближаются к А, то я утверждаю, что площади треугольников ABD и АСЕ будут в пределе относиться друг к другу, как квадраты сторон" (рис. 113).

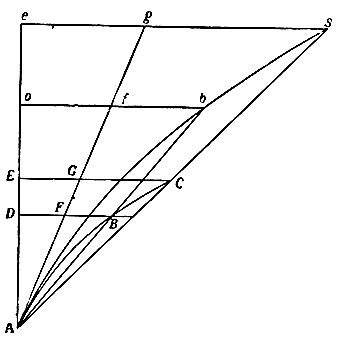
Рис. 113. Лемма IX

Опираясь на эту лемму о девиации, Ньютон доказывает, что пути, проходимые телом под действием силы за бесконечно малые промежутки времени, пропорциональны квадратам времён. Следовательно, и девиации (отклонения), вызванные действием сил за малые промежутки времени, пропорциональны квадратам времён. Последняя лемма, лемма XI этого раздела "Начал", утверждает:

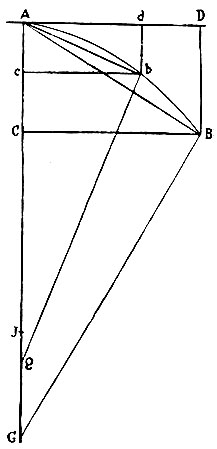
Рис. 114. Лемма XI

Расстояние от конца дуги до касательной, проведённой в её начале, при бесконечном уменьшении дуги для всех кривых, коих кривизна в точке касания конечная, пропорционально в пределе квадрату её хорды" (рис. 114).

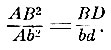
Излагая эти теоремы о пределах, Ньютон стремится избежать громоздкости геометрических доказательств от противного и грубости столе употребительного у его предшественников метода неделимых. Он говорит в "Поучении" к первой книге "Начал" следующее:

"Способом пределов достигается то же, что и способом неделимых, и после того как его основания доказаны, мы можем им пользоваться с ещё большею уверенностью. Поэтому, если во всем последующем изложении я и рассматриваю какие-либо величины как бы состоящими из постоянных частиц или если я принимаю за прямые линии весьма малые части кривых, то следует разуметь, что это не неделимое, а исчезающие делимые величины, что это не суммы и не отношения определённых конечных частей, а пределы сумм и пределы отношений исчезающих величин, и сущность этих доказательств в том и состоит, чтобы всё приводить к предыдущим леммам".

Введение в математику переменных величин посредством операций с их пределами считалось несовместимым с требованиями строгого геометрического доказательства. Ньютон стремится обосновать законность метода пределов апелляцией к механическому опыту:

"Делают возражение, что для исчезающих количеств не существует предельного отношения, ибо то отношение, которое они имеют ранее исчезания, не есть предельное, после же исчезания нет никакого отношения. Но при таком и столь же натянутом рассуждении окажется, что у тела, достигающего какого-либо места, где движение прекращается, не может быть "предельной" скорости, ибо та скорость, которую тело имело ранее, нежели оно достигло этого места, не есть "предельная", когда же достигло, то нет скорости. Ответ простой: под "предельной" скоростью надо разуметь ту, с которой тело движется не перед тем как достигнуть крайнего места, где движение прекращается, и не после того, а когда достигает, т. е. именно ту скорость, обладая которой тело достигает крайнего места, где движение прекращается. Подобно этому под предельным отношением исчезающих количеств должно быть разумеемо отношение количеств не перед тем, как они исчезают, и не после того, но при котором исчезают. Точно так же и предельное отношение зарождающихся количеств есть именно то, с которым они зарождаются. Предельная сумма зарождающихся или исчезающих количеств есть та составленная из них сумма, когда они, увеличиваясь или уменьшаясь, только начинают или прекращают быть. Существует такой предел, которого скорость в конце движения может достигнуть, но не может превзойти, это и есть предельная скорость. Такова же причина существования предела отношения зарождающихся или исчезающих количеств. Когда такой предел существует и величина его вполне определённая, то его нахождение есть задача истинно геометрическая. Всё же геометрическое может быть законным образом применяемо при геометрических изысканиях и доказательствах".

Механическая практика властно требовала внедрения новых математических методов, не считаясь с трудностями их логического обоснования. Компромиссный метод предельных отношений Ньютона оказался трудным и громоздким, и последующие механики стремились всё более и более прибегать к анализу, пока Лагранж не заявил с гордостью, что в его "Аналитической механике" нет ни одного чертежа. Так эволюционировал за сто лет математический аппарат механики. Задача же логического обоснования анализа была отодвинута до Дедекинда и Кантора.