Ньютоновы законы движения

Установив систему отсчёта, покоящуюся в абсолютном пространстве, Ньютон переходит к формулировке законов механики в этой системе. Эти знаменитые законы Ньютона формулируются им следующим образом.

"Всякое тело продолжает удерживаться в своём состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние".

Corpus otne perseverare in statu suo quiescendi vel movendi unifor-miter in directum, nisi quatenus illud a viribus impressis cogitur statum suum mutare.

"Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует".

Mutationem motus proportionalem esse vi motrici impressas, et fieri secundum Lineam rectam, qua vis ilia imprimatur.

"Действию всегда есть равное и противоположное про противодействие, иначе - взаимодействия двух тел друг на друга равны и направлены в противоположные стороны".

Actioni contrariam semper et aequalem esse reactionem: sive corporum duorum actionesin se mutuo semper esse aequales et in partes contrarias dirigi.

Стержнем ньютоновской динамики является второй закон, который математически можно записать так:

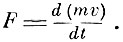
Сила, как указывает третий закон, всегда является взаимодействием между телами. Она определяется конфигурацией взаимодействующих тел, т. е. их массами и взаимными расстояниями. Она не будет зависеть от состояния тела и от наличия других сил. Отсюда вытекает в качестве следствия принцип суперпозиции сил, формулируемый Ньютоном в виде правила параллелограмма сил. Это следствие даёт возможность Ньютону перекинуть мост от динамики к статике; он трактует действие простых машин, разлагая и складывая действующие силы по правилу параллелограмма. Таким путём ой выводит закон равновесия косого рычага и действие наклонной плоскости. А это даёт возможность вывести "соотношения между усилиями в машинах, составленных из колёс, барабанов, воротов, рычагов, блоков, натянутых канатов и других механизмов, и весами грузов, поднимаемых или прямо, или наклонно, а также силы связок, приводящих в движение кости животных".

Из третьего и второго законов Ньютон выводит закон сохранения количества движения для замкнутой системы, т. е. системы, не подверженной действиям внешних сил, а только взаимодействиям тел, входящих в эту систему (следствие III). В следствии IV утверждается: "Центр тяжести системы двух или нескольких тел от взаимодействия тел друг на друга не изменяет ни своего состояния покоя, ни движения: поэтому центр тяжести системы всех действующих друг на друга тел (при отсутствии внешних действий и препятствий) или находится в покое, или движется равномерно и прямолинейно".

"Следовательно,- заключает Ньютон,- по отношению к центру тяжести системы нескольких тел имеет место тот же самый закон сохранения состояния покоя или равномерного и прямолинейного движения, как и для одного тела. Таким образом, поступательное количество движения отдельного ли тела, или системы тел надо всегда рассчитывать по движению центра тяжести". Так Ньютон устанавливает это весьма важное для динамики системы предложение.

Наконец, из принципа независимости действия сил и из того, что силы взаимодействия определяются только расстоянием между телами, вытекает классический принцип относительности Галилея-Ньютона.

Следствие V. "Относительные движения друг по отношению к другу тел, заключённых в каком-либо пространстве, одинаковы, покоится ли это пространство или движется равномерно и прямолинейно без вращения".

Точно так же относительное движение тел не изменяется, если приложить одновременно ко всем телам равные и одинаково направленные силы.

Раздел "Начал", посвященный изложению аксиом движения и ближайших следствий из них, заключается "Поучением", в котором идёт речь об опытной проверке законов движения. Первые два закона и вытекающий из них принцип независимости действия сил подтверждён опытами Галилея над падающими телами. Отправляясь от тех же законов, можно вывести формулу качания маятника, которая подтверждена уже практикой с часами. Третий закон динамики был подтверждён опытами Рена и Мариотта над ударами шаров. Сам Ньютон повторил эти опыты с большей точностью, введя поправку на сопротивление воздуха. Он нашёл, что "третий закон по отношению к удару и отражению подтверждается теорией, вполне согласующейся с опытом".

Подтверждается третий закон и для взаимодействий на расстояние. Если бы эти взаимодействия не были равны, то, поместив между взаимно притягивающимися телами препятствие, мешающее их сближению, можно было бы обнаружить, как это препятствие уступает действию большей силы. "Я производил подобный опыт с магнитом и железом; если их поместить каждый в отдельный сосуд и пустить плавать на спокойной воде так, чтобы сосуды взаимно касались, то ни тот, ни другой не приходят в движение, но вследствие равенства взаимного притяжения сосуды испытывают равные давления и остаются в равновесии". Точно так же, если бы взаимные притяжения частей Земли не уравновешивались, то Земля ушла бы ускоренным движением в бесконечность.

Ньютон считал особенно необходимым подтвердить экспериментально третий закон, как новый и впервые в отчётливой форме высказанный им. Этим объясняется и то, что он сам проделал опыты, подтверждающие этот закон, и то, что он указывает далее на большой опытный материал, доставляемый статическими машинами. "Подобно тому, как при ударе и отражении тела, коих скорости обратно пропорциональны массам, равнозначущи, так и при движении механических приборов действующие силы, коих скорости, взятые по направлению самих сил (проекции - скорости точки приложения каждой силы на направление этой силы), обратно пропорциональные этим силам, равнозначущи между собой, и при стремлении в противоположные стороны взаимно уравновешиваются. Так обстоит дело в рычаге, блоке, наклонной плоскости, винте, часах и во всякого рода машинах... Действительность и назначение машин в том только и состоит, чтобы, уменьшая скорость, увеличивать силу, и наоборот, ибо во всех подобного рода приборах в сущности решается такая задача: заданный груз двигать заданною силой или же заданное сопротивление преодолеть заданным усилием". И Ньютон заключает поучение многозначащим выводом:

"Дальнейшее изложение учения о машинах сюда не относится, я хотел лишь показать, сколь далеко простирается и сколь благонадёжен третий закон движения. Если действие движущей силы оценивать пропорционально произведению этой силы и скорости и подобно этому противодействие сопротивлений оценивать для каждой части в отдельности пропорционально произведению её скорости и встречаемого ею сопротивления, происходящего от трений, сцепления, веса и ускорения, то во всякой машине действие и противодействие будут постоянно равны, и поскольку действие передаётся машиной и в конце концов прилагается к сопротивляющемуся телу, то это последнее его значение будет обратно значению противодействия".

"В этих заключительных словах поучения,- комментирует акад. Крылов,- можно видеть не только начало возможных перемещений в его всеобъемлющем приложении к учению о равновесии машин, т. е. вообще систем тел с полной связью или одною степенью свободы, но и сущность принципа Даламбера, лишь высказанную в столь сжатой форме, что нужен был гений Лагранжа, чтобы это общее начало выразить одною математическою формулой, включающей в себя всю статику и динамику".

Так Ньютон привлекал для обоснования механики весь современный ему механический опыт. Законы Ньютона подтвердились дальнейшим развитием механики с исключительной точностью. Только в области больших скоростей, с одной стороны, и для весьма малых частиц - с другой, выявились отступления от ньютоновских законов. В области же механики земли и неба ньютоновы законы сохраняют полностью свою силу. Ближайшая задача состояла в том, чтобы развить со всей полнотой следствия из этих законов. Этой задаче и посвящено содержание "Начал".