Содержание первых двух книг "Начал"

"Начала" распадаются на три части: первые две части трактуют о движении тел, последняя часть посвящена системе мира. Первая часть книги разделена на четырнадцать отделов, вторая - на девять, третья часть на отделы не подразделяется.

Первый отдел первой книги озаглавлен "О методе первых и последних отношений, при помощи которого последующее доказывается". Отдел посвящен изложению математического аппарата, его содержание было рассмотрено нами выше.

Второй отдел посвящен вопросу нахождения центростремительных сил. В первых предложениях этого раздела устанавливается связь между теоремой площадей и центральным характером силы (теоремы I, II, III). Вывод, к которому приходит Ньютон в результате доказанных предложений, сформулирован в коротком "Поучении": "Так как равномерное описание площадей служит указателем центра, к которому направляется оказывающая наибольшее влияние на движущееся тело сила, которою оно и отклоняется от прямолинейного пути и удерживается на своей орбите, то почему бы не принять в последующем равномерное описание площадей вообще за признак центра, около которого происходит всякое круговое движение в свободном пространстве".

В четвёртом предложении выводится выражение для центростремительной силы, найденное впервые Гюйгенсом, как указывает и Ньютон в "Поучении" к этому предложению. В последующих предложениях даются вспомогательные формулы для расчёта центростремительных сил.

Третий отдел первой книги посвящен выводу закона центростремительной силы из законов Кеплера. Здесь устанавливается, что движение тела по коническому сечению: эллипсу, гиперболе, параболе - поддерживается силой, направленной к фокусу и обратно пропорциональной квадрату расстояния от этого фокуса. Доказывается, что этот же закон силы приводит и к третьему закону Кеплера. В последнем предложении отдела указывается способ определения орбиты тела, находящегося под действием центростремительной силы, обратно пропорциональной квадрату расстояния от центра сил, и выходящего из заданного положения с заданной скоростью. В зависимости от величины скорости орбита тела будет эллипсом, параболой или гиперболой. В следствиях указываются методы учёта действия возмущающих сил.

Четвёртый и пятый отделы посвящены чисто геометрическим вопросам определения орбит по известным данным. Отдел VI озаглавлен "Об определении движения по заданным орбитам" и посвящен вопросу нахождения уравнения движения тела по заданной орбите: параболической и эллиптической.

Седьмой отдел посвящен исследованию прямолинейного движения тела, подверженного действию центральной силы. Здесь Ньютон чисто геометрическим путём решает задачу об определении движения тела, притягиваемого или отталкиваемого силовым центром, если начальная скорость его направлена к центру. Заключительное предложение этого отдела формулировано в виде следующей задачи:

"Предполагая центростремительную силу какою угодно и допуская квадратуру кривых, требуется определить как скорость движущегося прямо к центру или от центра тела в любой точке, так и время, в течение которого оно приходит в какое-либо место и обратно".

Чтобы дать представление о геометрическом методе Ньютона, приведём найденное им решение задачи.

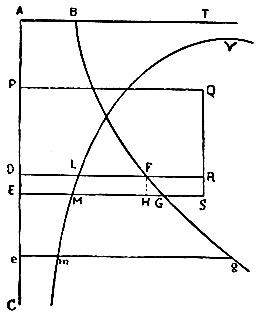
Рис. 121. К предложению XXXIX

"Из какой-либо заданной точки А по прямой ADEC падает тело. Из всякой точки Е его пути (рис. 121) восставляется перпендикуляр EG, по коему откладывается длина EG, пропорциональная величине центростремительной силы, действующей в этой точке Е и направленной к центру С; пусть кривая BFG проходит через места точек G, причём в начале движения EG совпадает с перпендикуляром АВ; тогда скорость в какой угодно точке Е будет пропорциональна стороне квадрата, равномерного с криволинейною площадью АВСЕ.

Беря на прямой EG длину ЕМ, обратно пропорциональную стороне сказанного квадрата, строится кривая, на которой постоянно лежит точка М. Эта кривая будет иметь прямую А В своей асимптотою. Время, в течение которого падающее тело проходит путь АЕ, будет пропорционально площади ABTV ME".

Поясним решение. Пусть начальная скорость тела равна нулю, начальное расстояние от центра АС = х0. Массу тела примем за единицу. Тогда для любого момента времени имеем:

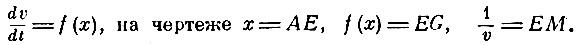
В начальный момент времени

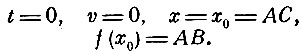
Имеем

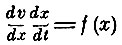
или

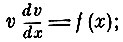
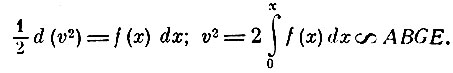
Этим и доказывается первая часть найденного Ньютоном решения. Таким образом, предложение Ньютона представляет собой не что иное, как теорему живых сил для прямолинейного центрального движения. Далее

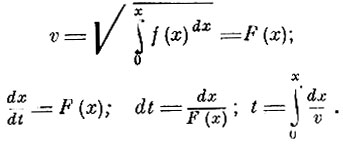
Этим доказывается вторая часть найденного Ньютоном решения. Ньютон, следовательно, впервые находит теорему живых сил и впервые представляет работу площадью. Ему же принадлежит применение этой теоремы к нахождению закона движения (первый интеграл уравнений движения). Этот результат Ньютон обобщает в следующем, восьмом отделе "Начал" на случай любого закона центральных сил и любой начальной скорости. Предложение XL, теорема XIII "Начал" выражает найденную Ньютоном консервативность поля центральных сил:

"Если тело под действием какой угодно центростремительной силы движется как бы то ни было, другое же тело движется прямолинейно, прямо к центру или от центра, и скорости обоих тел в некотором их положении, в котором они равноудалены от центра сил, равны, то эти скорости будут равны и во всяких других положениях обоих тел, равноудалённых от центра".

В самом деле, теорема живых сил даёт:

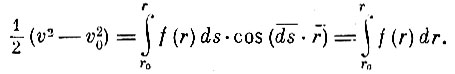
Ньютон проводит доказательство геометрически, разлагая силу, действующую в какой-либо точке траектории тела, на нормальную и касательную составляющие. Нормальная составляющая не меняет скорости тела по величине, а будет лишь уклонять его от прямолинейного пути и заставлять, непрерывно отступая от касательной к орбите, описывать криволинейный путь. Вся эта сила и поглощается на производство этого действия". Отсюда видно, насколько ясно Ньютон представляет здесь понятие работы. Нормальная составляющая сила работы не производит, работа же тангенциальной силы идёт на ускорение тела, причём приращения скорости оказываются зависящими только от расстояния его от центра. В следствии из этого предложения Ньютон указывает, что если центростремительная сила пропорциональна какой-либо степени А^n-1, коей показатель n-1 есть любое число n, уменьшенное на 1, тогда при всяком расстоянии А скорость тела будет пропорциональна 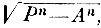где Р - наибольшее расстояние тела от силового центра, на которое может удалиться качающееся или обращающееся по какой-либо траектории тело, если бы его в какой-либо точке подбросить прямо от центра с тою скоростью, которою оно в этой точке обладает. Действительно, по теореме живых сил: т

Этой теоремой Ньютон пользуется для решения следующих задач.

"Предполагая центростремительную силу какою угодно и допуская квадратуру кривых, требуется найти как траекторию, по которой будет двигаться тело, так и закон его движения по найденной траектории".

"При заданном законе центростремительной силы требуется определить движение тела, выходящего из заданного места с заданною по величине и направлению скоростью".

Девятый отдел "Начал" посвящен рассмотрению движения тела по вращающимся орбитам.

В десятом отделе, озаглавленном "О движении тел по заданным поверхностям и о колебательном движении подвешенных тел", рассматривается задача маятника. Ньютон рассматривает здесь циклоидальный маятник Гюйгенса. В заключительном предложении этого раздела рассматривается несвободное движение точки под действием центральной силы.

Одиннадцатый отдел "О движении тел, взаимно притягивающихся центростремительными силами", ставит во всей общности задачу центрального движения. Вначале изучается задача движения двух тел, в предложении же LXV формулируются условия, при которых "несколько взаимодействующих по закону обратной пропорциональности квадрату расстояния тел могут двигаться по эллипсам, описывая радиусами, проведёнными к фокусу, площади, весьма близкие к пропорциональности времени". Эти условия выполняются, когда несколько малых тел обращаются "около какого-нибудь большого в различных от него расстояниях и... притягиваются друг к другу пропорционально своим массам". Таким образом, это предложение имеет исключительное значение для теории солнечной системы. Последующее предложение играет фундаментальную роль в теории Луны.

"Если три тела притягиваются взаимно с силами, обратно пропорциональными квадратам расстояний, и оба меньших обращаются вокруг третьего наибольшего, то площади, описываемые радиусом, проводимым от среднего и ближайшего к наибольшему, будут ближе к пропорциональности временам, и его траектория ближе к эллипсу, в фокусе которого сходятся эти радиусы, когда это наибольшее тело будет двигаться под действием сказанных притяжений, нежели в том случае, когда оно, не испытывая притяжений от малых тел, оставалось бы в покое, или же, будучи притягиваемо или значительно сильнее, или значительно слабее, совершало бы или гораздо большие, или гораздо меньшие движения".

В следствиях из этого предложения рассматриваются неравенства движения Луны и даётся теория приливов и отливов. В целом одиннадцатый отдел "Начал" является основоположным отделом теоретической астрономии. Проблема тяготения здесь ставится во всей её полноте. Ньютон приходит к фундаментальному выводу о "пропорциональности между центростремительными силами и массами тех центральных тел, к которым эти силы направляются". Подробнее вопрос о тяготении исследуется в разделе "Система мира".

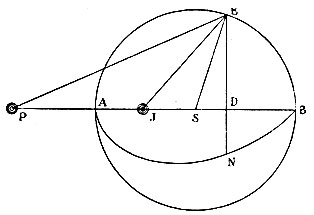
Рис. 122. К предложению LXXXII

В двенадцатом отделе "О притягательных силах сферических тел" Ньютоном закладываются основы теории потенциала. Ньютон доказывает здесь, что сферический слой не действует на внутреннюю точку, на внешнюю же - так, как если бы вся его масса была сосредоточена в центре (при условии, что элементарный закон тяготения сводится к обратной пропорциональности квадрату расстояния взаимодействующих частиц и прямой пропорциональности произведению масс). Точно так же он устанавливает, что действие шара на внутреннюю точку пропорционально ее расстоянию от центра, и на внешнюю - обратно пропорционально квадрату расстояния от центра. Рассматриваются случаи взаимодействия шаров и способы подсчёта действия шара на точку. В предложении LXXXII формулируется теорема XLI, послужившая В, Томсону основой для его метода электрических изображений^*. Короче говоря, основы теории потенциального силового поля были заложены Ньютоном в этом и последующем, тринадцатом разделе "Начал", трактующем "О притяжении тел несферических".

^* (Это предложение гласит:

"Если для шара, коего центр S и радиус SA, взять расстояние SJ и SP так" чтобы было

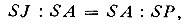
то отношение притяжения шаром внутренней точки J к притяжению внешней точки Р равно произведению отношения на корень квадратный из отношения притяжений точек Р и J центром шара".

Точка J по отношению к точке Р (рис. 122) названа Томсоном "Электрическим изображением".)

Первая книга "Начал" заканчивается четырнадцатым отделом "О движении весьма малых тел под действием центростремительных сил, направленных к отдельным частицам весьма большого тела". Отдел этот представляет особый интерес, так как по существу он даёт механическую основу ньютоновой оптики. Отдел открывается следующим предложением:

"Если две однородные среды разделяются пространством, заключённым между двумя параллельными плоскостями, и тело, при переходе через это пространство притягивается или побуждается к одной из средин перпендикулярно к плоскости раздела, других же сил к нему никаких не приложено, и если при этом притяжение, при всяком расстоянии от обеих плоскостей, одно и то же и направлено в ту же сторону, то синус угла падения на первую плоскость находится в постоянном отношении к синусу угла выхода из второй" (рис. 123).

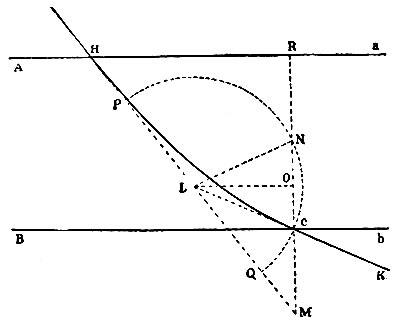
Рис. 123. К предложению XCIV

Таким образом, если обозначить скорость частицы при падении на первую плоскость через v₀, угол падения через α₀, скорость частицы по выходе - через V, угол выхода через α, то предложение Ньютона запишется в виде закона преломления:

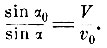
Это равенство легко получить из уравнений движения частицы, если принять за ось z перпендикуляр к поверхности раздела, а за ось х-линию пересечения плоскости падения с плоскостью раздела. Принимая, что сила притяжения является функцией z и действует на всём расстоянии h между граничными плоскостями, получим уравнения движения частицы:

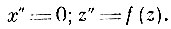(1)

Начальные условия: при t = 0 х = 0, z = 0,

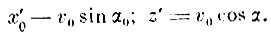(2)

По теореме живых сил:

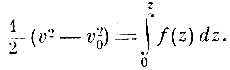
(3)

При

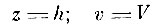
и направление движения составляет угол α с осью z. На основании уравнения (2)

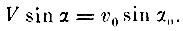(4)

По уравнению же (3)

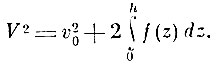
Уравнение (4) даёт

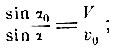
следовательно, скорость частицы в более плотной среде возрастает. У Ньютона смысл постоянного отношения синусов раскрывается в предложении XCV.

"При тех же предложениях я утверждаю, что скорость частицы до падения относится к ее скорости после выхода, как синус угла выхода к синусу угла падения".

Известно, что в теории Гюйгенса отношение синусов оказывается равным прямому отношению скоростей, а не обратному, как это получается у Ньютона. Поэтому в качестве experimentum crucis мог бы служить опыт по измерению скоростей света в воздухе и воде. Как известно, опыт Фуко решил вопрос в пользу теории Гюйгенса.

Следующее предложение трактует о полном отражении.

"Предполагая то же, что и ранее, и что скорость движения до падения больше скорости после такового, утверждаю, что можно настолько увеличить наклонение линии падения, что частица будет отражаться, причём угол отражения будет равен углу падения" (рис. 124).

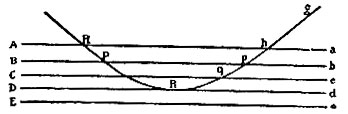
Рис. 124. К предложению XCVI

В "Поучении" Ньютон указывает, что "от изложенных выше движений частицы почти не отличается отражение и преломление света, совершающееся в постоянном отношении секансов, как это найдено Снеллиусом, следовательно, и в постоянном отношении синусов, как это изложено Декартом"" Это может служить основанием для принятия корпускулярной теории света. Другим основанием может служить то обстоятельство, что скорость света, по наблюдениям Рёмера, оказалась конечной, а не бесконечной, как полагал Декарт. Наконец, третьим доводом, о котором также упоминается в "Поучении", являются дифракционные явления, открытые Гримальди. "Когда... лучи находятся в воздухе... то при лучи находятся в воздухе... то при проходе близ углов тел непрозрачных или прозрачных... они загибаются в сторону к телу, как бы будучи к нему притягиваемыми". Но Ньютон, переходя к изложению двух предложений, касающихся геометрической оптики, снова делает оговорку, что он не будет касаться "самой природы лучей" (телесная она или нет). Предложения оптики он будет устанавливать, "совершенно её не обсуждая, а только находя пути тел, подобные ходу лучей". Таким образом, Ньютон рассматривает корпускулярную теорию как формальную, удобную для описания световых явлений, но не претендующую на более глубокое значение.

Этим отделом и заканчивается первая книга "Начал". Если в ней трактовалось потенциальное поле в вакууме, то во второй книге рассматривается влияние среды. Это влияние прежде всего сказывается в возникновении сил сопротивления (внутреннего трения), зависящих от скорости движущегося в среде тела. Учёт этого влияния производится с помощью эмпирических формул. В первом отделе принимается, что силы сопротивления пропорциональны скорости. В первых предложениях этого отдела изучается действие таких сил. Устанавливается, что изменение количества движения, вызываемое такими силами, пропорционально пройденному телом пути^* и что скорость убывает в геометрической прогрессии^**. Рассматриваются задачи, имеющие важное значение для баллистики, а именно: движение тела, брошенного вверх, и движение тела, брошенного под углом.

^* (В самом деле, если

)

^** ()

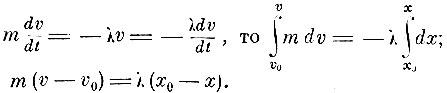
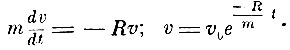"Впрочем,- заключает Ньютон в "Поучении" к этому отделу,- предположение, что сопротивление пропорционально скорости, более математическое, нежели соответствующее природе". Более соответствующим природе будет предположение, что силы сопротивления будут пропорциональны квадрату скорости. Второй отдел и посвящен вопросу движения тел при сопротивлении, пропорциональном квадрату скорости. В этом отделе Ньютон вводит свой метод исчисления флюксий. Сложную задачу отыскания баллистической кривой Ньютон заменяет другой, несколько искусственной: "Отыскать закон изменения плотности среды, в которой тело двигалось бы по заданной кривой".

В третьем отделе закон сопротивления задаётся многочленом

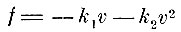
и даются геометрические приёмы вычисления путей, проходимых телом, брошенным вверх.

В четвёртом отделе рассматривается вопрос о круговом движении в сопротивляющейся среде. Это будет движение по спирали, пересекающей радиусы-векторы под постоянным углом; при этом центростремительная сила принимается пропорциональной n-й степени плотности, плотность среды обратно пропорциональна расстоянию от центра, сопротивление пропорционально плотности.

Пятый отдел посвящен гидростатике. Вначале даётся определение жидкости:

"Жидкость есть такое тело, коего части уступают всякой как бы то ни было приложенной силе, и уступая, свободно движутся друг относительно друга". Отсюда выводится равномерное распределение давлений (в невесомой жидкости) и вычисляется давление на дно, производимое тяжёлой жидкостью. В предложении XXI, теорема XVI, устанавливается закон распределения плотностей жидкости, находящейся в поле центростремительных сил, обратно пропорциональных квадрату расстояния. При этом жидкость подчиняется закону Бойля-Мариотта: плотность пропорциональна давлению. Частным случаем найденного Ньютоном распределения будет барометрическая формула, впервые полученная Галлеем. В заключительном предложении отдела Ньютон исследует закон взаимодействия частиц, образующих жидкость, подчиняющуюся закону Бойля. В предложении устанавливается, что плотность жидкости будет пропорциональна давлению, если частичные отталкивательные силы обратно пропорциональны расстоянию между частицами. Эти силы, подобно магнитным силам, действуют на очень малом расстоянии, на более же отдалённые частицы не оказывают никакого влияния. Здесь мы имеем интересную попытку Ньютона вывести из молекулярно-атомной гипотезы закон Бойля^*. Такая проблема для Ньютона не случайна. Мы увидим далее, что она целиком и полностью вытекает из его натурфилософских концепций. Но, как и всюду в "Началах", Ньютон стремится избежать категорических суждений и заканчивает раздел о жидкостях таким характерным замечанием: "Состоят ли жидкости из взаимно отталкивающихся частиц - есть вопрос физический. Мы доказали математически свойства жидкостей, состоящих из таких частиц, и предоставляем физикам повод исследовать этот вопрос".

^* (Правда, не из кинетических соображений. Эта задача решается им как статическая.)

Шестой отдел посвящен изучению затухающих колебаний маятников в сопротивляющейся среде. Этот вопрос Ньютон исследовал весьма тщательно, проделывая опыты над изучением качания маятников в сопротивляющейся среде, справедливо полагая, что подобные исследования дают материал для характеристики сопротивления среды. Кроме того, опыты с маятниками дают возможность исследовать весьма точно вопрос о пропорциональности массы и веса. Сопротивление среды интересовало Ньютона и как важная практическая проблема (наилучшая форма обтекаемости судов), и как проблема, имеющая крупное философское значение в связи с гипотезой эфира. Любопытна в связи с этим попытка Ньютона сравнить сопротивление воздуха с сопротивлением эфира. Сопротивление воздуха действует на наружную поверхность тела, эфир же, проникая в поры между частицами тел, должен вызывать и внутреннее сопротивление. "Поэтому я произвёл испытания, чтобы определить, сосредоточено ли полностью сопротивление, испытываемое телами при движении, на их наружной поверхности, или же и внутренние части тел претерпевают заметное сопротивление". Ньютон измерял сопротивление порожней еловой кадочки, качающейся на нити в 11 футов длиной, и сопротивление той же кадочки, заполненной металлом. Он пришёл к заключению, что сопротивление на наружную поверхность в 5 тысяч с лишним раз больше сопротивления на внутренние частицы.

В седьмом отделе "О движении жидкостей и сопротивлении брошенных тел" рассматривается механизм сопротивления и влияние формы тела на сопротивление, испытываемое им при движении в жидкости. Здесь, следовательно, Ньютон ставит важные и трудные вопросы гидродинамики вязкой жидкости, для решения которых ещё не было в его время достаточных экспериментальных данных и необходимых математических средств. Но гений Ньютона и здесь наметил пути решения поставленных задач. Он начинает раздел с формулировки теоремы о подобии, а известно, какое огромное значение имеет теория подобия в современной гидро- и аэродинамике. Переходя к вопросу о влиянии размеров, скоростей тел и плотностей сред, Ньютон исходит из гипотезы о механизме сопротивления. По Ньютону, "сопротивление происходит частью от центробежных и центростремительных сил взаимодействия между частицами, частью от ударов частиц о большие части систем и отражений от них. Сопротивления первого рода будут пропорциональны квадратам скоростей, квадратам сходственных измерений и плотностям частей систем". "Сопротивления второго рода пропорциональны числу и силе соответствующих ударов и отражений". В результате оказывается, "что сопротивления, испытываемые соответствующими частями систем, относятся между собой, как произведения квадратов скоростей на квадраты линейных измерений и на плотности частей". Изучая влияние формы тела на сопротивление и установив, что сопротивление шара, при равных диаметрах и скоростях, вдвое меньше сопротивления цилиндра, Ньютон ставит задачу нахождения наиболее обтекаемой формы, подходя к вариационным проблемам. Не останавливаясь на ошибочной теории Ньютона истечения жидкости из отверстия в дне сосуда, укажем, что последние предложения этого раздела посвящены изучению движения шара в вязкой жидкости. Этот вопрос интересовал Ньютона постольку, поскольку он давал возможность экспериментального исследования вязкостей жидкости по временам падения шаров. В результате своих исследований Ньютон приходит к выводу, что гипотеза эфира несовместима с движением планет.

"Небесные пространства, через которые планетные и кометные шары повсюду непрестанно движутся совершенно свободно и без всякого заметного уменьшения своего количества движения, совершенно лишены какой-либо телесной жидкости, за исключением, может быть, чрезвычайно тонких паров и пронизывающих эти пространства световых лучей".

Восьмой отдел посвящен изучению волнового движения в жидкой среде. Прежде всего Ньютон устанавливает, что движение в жидкости может передаваться и не по прямой линии.

"Давление не распространяется через жидкость прямолинейно, если только частицы жидкости не лежат на одной прямой".

"Всякое движение, распространяющееся через жидкость, отклоняется от прямого Пути в области, занятые неподвижной жидкостью".

Далее Ньютон изучает волны, создаваемые в среде колеблющимся источником. Для водяных волн, частицы которых движутся по круговым путям, Ньютон устанавливает пропорциональность скорости распространения корню квадратному из длины волны. Рассматривая распространение гармонических колебаний в газах, Ньютон устанавливает, что скорость распространения будет прямо пропорциональна корню квадратному из упругости среды и обратно пропорциональна корню квадратному из плотности. Предполагая справедливым для среды закон Бойля, он выводит формулу для скорости звука в газе:

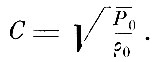
Вычисления по этой формуле не дают правильного результата. Ньютон не нашёл удовлетворительного объяснения этому расхождению, которое, как показал Лаплас, обусловлено тем, что процесс распространения волны не является изотермическим и что удовлетворительный результат получается, если принять, что сгущения и разрежения происходят адиабатически.

Последний, девятый отдел "Начал" посвящен рассмотрению вихревых движений в жидкостях. Цель этого раздела - выяснить, насколько согласуется вихревая гипотеза Декарта с законами Кеплера. Правда, у Ньютона ещё не было столь важного для теории вращательного движения понятия момента количества движения, и поэтому в его расчёты вкралась ошибка; тем не менее, вычисления угловых скоростей вращения частиц жидкости на различных расстояниях от вращающегося шара не приводят к третьему закону Кеплера. Ньютон показывает, что "если в однородной и беспредельной жидкости вращается равномерно около постоянной оси твёрдый шар, и жидкость приводится во вращательное движение единственно только этим натиском, и всякая её часть продолжает сохранять своё равномерное движение, то... времена оборотов частиц жидкости будут пропорциональны квадратам их расстояний до центра шара". Расчёт Ньютона основан на законе количества движения, если же заменить его законом момента количества движения, то указанная пропорциональность будет не квадратной, а кубической. "Пусть философы сами посмотрят,- заключает Ньютон,- при каком условии может быть объяснено вихрями явление, заключающееся в существовании указанного полукубического отношения" (т. е. третьего закона Кеплера).

Далее Ньютон устанавливает, что благодаря действию центробежных сил "тела, которые при переносе вихрем описывают постоянно одну и ту же орбиту, должны обладать одинаковою с вихрем плотностью и двигаться по тому же закону скорости и её направления, как и части самого вихря".

"Следовательно, тело, обращающееся вместе с вихрем по неизменной орбите, находится в покое по отношению к жидкости, в которой оно плавает".

"Если вихрь повсюду одинаковой плотности, то то же самое тело может обращаться на любом расстоянии от центра". А значит, планеты не могут переноситься вихрями, так как они движутся по законам Кеплера, которым не удовлетворяют части вихря. "Таким образом, гипотеза вихрей совершенно противоречит астрономическим явлениям и приводит не столько к объяснению движений небесных тел, сколько к их запутыванию. Способ, которым эти движения совершаются на самом деле в свободном пространстве, можно понять по первой книге, подробнее же он рассматривается в изложении "Системы мира".

Таково содержание "Начал"^*. По богатству содержания, по глубине и напряжённости мысли это произведение принадлежит к числу немногих созданий человеческого гения. Научный подвиг Ньютона был по справедливости оценён современниками. Но и потомки не переставали черпать из этой сокровищницы физической мысли, какой являются "Начала". Метод Ньютона служил примером Амперу и Фарадею, Томсону и Максвеллу, Эйнштейну и Дираку. И на долгие времена идейное богатство "Начал" будет вдохновлять творческую физическую мысль.

^* (Третья книга "Начал" посвящена изложению "Системы мира". Она распадается на две части, одна из которых представляет собой интерес для характеристики натурфилософских воззрений Ньютона и будет рассмотрена нами в связи с анализом этих воззрений. Вторая же часть - астрономическая - не является темой нашего очерка.)