Новые открытия в акустике и оптике

Явления внешней теплопроводности, исследованные теоретически Фурье и экспериментально Дюлонгом и Пти, обусловлены в одной своей части лучеиспусканием. Учение о лучистой теплоте начало формироваться на грани XVIII и XIX в. и в этот период было обогащено важными открытиями, истинное значение которых было оценено через столетие.

Термин "лучистая теплота" и первые наблюдения над тепловыми лучами принадлежат химику Шееле, который в своём "Химическом трактате о воздухе и огне" (1777), наряду со своим сообщением об открытом им кислороде, трактует и о тепловых лучах. Он указывает, что воздух не согревается от тепловых лучей, что стеклянное зеркало не отражает тепловых лучей. Ещё раньше Ламберт заметил, что стекло задерживает тепловые лучи, подтвердив опыт металлургов, защищающих глаза от сильного жара стеклянными очками. Металлическое же зеркало, по наблюдениям Шееле, отражает тепловые лучи, оставаясь само холодным.

Следующие исследования теплового лучеиспускания принадлежат Пикте (1752-1825). Пикте, установив два вогнутых металлических "зеркала Пикте" параллельно друг другу и помещая в фокусе одного зеркала термометр, а в фокусе другого попеременно то нагретое, то охлаждённое тело, обнаружил соответственно повышение и понижение температуры термометра, причём помещённый вблизи фокуса контрольный термометр показывал неизменную температуру. Эффект усиливался, если шарик термометра был зачернён. Пикте также установил, что опыт не удаётся со стеклянными зеркалами, а стеклянная пластинка преграждала путь тепловым лучам.

"Опыты об огне" Пикте вышли в 1790 г., а в следующем 1791 г. аббат Прево (1751-1839),основываясь на опытах Пикте,установил свою теорию "равновесия огня". Согласно Прево, нагретое тело испускает тепловые лучи, распространяющиеся по законам обычных лучей света. Каждое тело излучает теплоту и одновременно поглощает теплоту из окружающего пространства. Чем выше температура тела, тем больше оно теряет тепла лучами, нежели заимствует из окружающего, холодное же тело, наоборот, больше заимствует теплоты из окружающего пространства, чем отдаёт. Вследствие этого осуществляется перенос теплоты лучами от нагретых тел к холодным. При тепловом равновесии тело столько же поглощает тепла, сколько и излучает, и его температура остаётся неизменной.

Нет ничего удивительного, что Прево пришёл к мысли о сходстве тепловых и световых лучей: огонь порождает свет и тепло. Теория Прево получила ещё большую поддержку в блестящем открытии Гершеля, который исследовал нагревательную способность различных частей солнечного спектра. Оказалось, что чувствительные термометры, помещённые в различных участках спектра, нагреваются не одинаково, температура растёт к красному концу спектра, повышение температуры отмечалось и за пределами спектра. Тогда Гершель направил развёрнутый в спектр световой поток на линзу, в фокусе которой был помещён шарик термометра. Половина линзы была прикрыта папкой, так что весь видимый поток падал на папку. Если красная граница спектра была удалена на ¹/₁₀ дюйма от края папки, то температура термометра повышалась на 45°, причём наблюдалась дифракция от края экрана, шарик был освещен слабым красноватым светом. Дифракция исчезала,если граница видимого спектра была отодвинута на ¹/₅ дюйма, температура же повышалась в этом случае на 21°.

Отсюда Гефшель сделал вывод о существовании в спектре невидимых лучей, распространяющихся по законам световых лучей и производящих сильное тепловое действие. Так были открыты инфракрасные лучи.

Рис. 192. Кубик Лесли

Однако были и противники теории невидимых тепловых лучей. Так, например, Лесли (1766-1832) считал, что самая идея невидимых лучей содержит внутреннее противоречие. В своих исследованиях с изобретённым им кубиком и дифференциальным термометром он, однако, положил начало количественному исследованию лучеиспускательной способности. Аналогичными исследованиями занимался Румфорд. И Лесли и Румфорд пришли к выводу, что излучательная способность тел тем ниже, чем выше их отражательная способность.

Лесли, гаким образом, по существу продолжал исследования Прево. Значительно серьёзнее были другие факты, свидетельствующие, что свет и тепло - не одно и то же. К ним относятся в первую очередь загадочные явления фосфоресценции и флюоресценции, открытые ещё в первой половине XVII в. В XVIII в. эти явления изучались Петровым, Веджвудом, Гротгусом. Теории явления были предложены Босковичем, Эйлером, Гротгусом, однако сущность этих сложных процессов осталась скрытой.

С другой стороны, было открыто поглощение света без нагревания. В 1785 г. Сенбьё открыл почернение хлористого серебра на свету. Риттер, исследуя действие различных частей спектра на хлористое серебро, обнаружил, что красные лучи химически не активны, что химическая активность лучей возрастает к фиолетовому концу и что за фиолетовым концом спектра имеются невидимые очень активные химические лучи.

Эти "химические" лучи были открыты одновременно Волластоном (1801). Таким образом, область спектра была расширена как в сторону инфракрасных лучей, так и в сторону ультрафиолетовых. Тот же Волластон в 1802 г. открыл "фраунгоферовы" линии, которые он считал границами цветов. Границы красного цвета Волластон обозначил через А (внешняя неясная граница) и В, отделяющая красную часть от следующей, желто-зелёной, которая отделяется от синей линией С. Линия D отделяет синюю часть от фиолетовой, граница которой Е. "Впрочем,- заключает Волластон,- бесполезно подробнее описывать явления, меняющиеся в зависимости от яркости света и объяснение которых я не могу принять на себя". Кроме того, Волластон полагал, что спектры раскалённых тел и электрического света также непрерывны. Поэтому история физики с полным правом приписывает открытие линий поглощения в солнечном спектре сыну стекольщика, оптическому мастеру Фраунгоферу (6 марта 1787 г.- 7 июня 1826 г.), опубликовавшему своё открытие в 1814 г.

Прежде чем перейти к изложению нового этапа борьбы двух концепций в оптике, изобилующего острыми драматическими моментами, мы должны рассмотреть состояние учения о механических колебаниях и волнах на рубеже XVIII-XIX вв., и в частности состояние акустики.

Математическая теория колебаний и волн в конце XVIII в. значительно продвинулась вперёд благодаря Лагранжу. В "Аналитической механике" один из разделов посвящен теории малых колебаний, последние разделы труда посвящены гидродинамике несжимаемой жидкости и гидродинамике упругих жидкостей. Однако разработка теории упругой среды началась только в XIX в. (Пуассон, Навье, Коши). С другой стороны, изучение специально акустических колебаний ограничивалось струной и трубами. В струне рассматривались поперечные колебания; только Рикатти (1767) заметил, что звучащая струна попеременно то укорачивается, то удлиняется. Вообще можно сделать вывод, что акустические проблемы XVIII в. составляли прерогативу математиков и музыкантов.

Первым систематическим трудом по акустике было сочинение Хладни (1756-1827) "Акустика", вышедшее в 1802 г. Хладни рассматривает различные источники звука, устанавливает важный факт существования продольных колебаний, а на цилиндрических стержнях и вращательных колебаний. Он дал первую теорию камертона, наконец ему принадлежит первый экспериментальный способ изучения колебаний в пластинках, известный под названием "хладниевы фигуры".

Именно это открытие доставило Хладни большую известность. Лаплас придавал большое значение замечательному эксперименту Хладни. Наполеон отпустил Хладни средства на издание его акустики на французском языке. Институт не замедлил объявить конкурсную задачу: найти математическую теорию хладниевых фигур. Но эта задача оказалась не под силу даже такому математику, как Пуассон. Только в 1883 г. Уитстону удалось дать теорию явления.

Любопытно, что опорные пункты и стимулы к математической разработке упругих колебаний и волн дала все-таки не акустика, а оптика. И здесь мы переходим к изложению переворота в оптических воззрениях, произошедшего в первой трети XIX в.

Начало борьбы было положено Томасом Юнгом, человеком изумительных и разносторонних дарований. Его биография в связи с этим, приобретает несомненный интерес.

Юнг родился 13 июня 1773 г. Детство своё он провёл у деда по матери, купца. Двух лет от роду Юнг научился читать^*, на шестом году он учился литературе у бристольского профессора, на восьмом году Юнг заинтересовался землемерными работами, которыми занимался его сосед-геодезист, и скоро научился искусству определять расстояния и вычислять высоты. С 9 до 14 лет Юнг жил в пансионе в Комптоне у профессора Томсона. За этот период Юнг изучал греческих и римских классиков, изучил французский, итальянский, древнееврейский, персидский и арабский языки. Увлекшись ботаникой, он задумал сам построить микроскоп и с этой целью изучил токарное ремесло и дифференциальное исчисление(!). В этот же период Юнг написал обстоятельный разбор систем греческой философии. Выбирая профессию, Юнг решил остановиться на медицине, которую он изучал в Лондоне, Эдинбурге и Лейпциге, где и получил в 1795 г. степень доктора медицины. Но ещё в 1793 г. он поместил в "Phil. Trans." работу по физиологической оптике "Наблюдения над процессом зрения". В этой работе Юнг занимался проблемой аккомодации. Этот вопрос тогда был очень спорным и неясным. Кеплер, Декарт и ряд других учёных считали, что аккомодация обусловлена деформацией глаза как целого; Потерфильд да и другие считали, что аккомодация обусловлена перемещением хрусталика; Жюрен и Мушенброк считали причиной аккомодации изменение кривизны роговой оболочки; Соваж и Бурдело усматривали эту причину в изменении кривизны хрусталика.

^* (См. биографию Юнга в "Биографиях" Араго.)

К этому последнему мнению примкнул и Юнг, обосновав его тщательным изучением анатомии глаза и в особенности хрусталика. Теория Юнга вызвала шумные отклики. С одной стороны, появились притязания на первенство открытия, с другой - анатом Гом и оптик Рамсден представили доказательства неизменяемости хрусталика.

Юнг был вынужден отказаться от своей теории, однако в 1800 г. он взял отказ обратно и новыми опытами обосновал справедливость своего воззрения. В это же время сложились у него воззрения на природу света. С 1801 по 1804г. Юнг - профессор Королевского института и автор принципа интерференции. В это же время он даёт ключ к разгадке египетских иероглифов. В 1807 г. вышел фундаментальный двухтомный труд Юнга "Лекции по натуральной философии". С 1818 г. он - секретарь бюро долгот и редактор знаменитого "Nautic. Alman." (мореходный календарь). Напряжённый труд по этому изданию не принёс Юнгу ничего, кроме несправедливых обвинений. В результате этих нападок Комиссия долгот была распущена, и хотя Юнга снова призвали к изданию календаря, всё же эта история тяжело отразилась на его здоровьи. Юнг умер 10 мая 1829 г.

Девизом Юнга было: "всякий человек, может сделать то, что делают другие". Следуя этому девизу, Юнг, например, сделался цирковым наездником, канатоходцем и привлекал в знаменитом цирке Франкони многочисленную публику. Он был прекрасным музыкантом и играл почти на всех известных в его времена музыкальных инструментах. Глубокий знаток живописи, он знал всех мастеров этого искусства, до мельчайших деталей их творчества. В его сочинениях разбираются вопросы механики, оптики, акустики, теплоты, физиологической оптики, технологии, кораблестроения, астрономии, геофизики, медицины, филологии, зоологии и пр. Им было написано около 60 глав для приложений к "Британской энциклопедии".

При этом Юнг отнюдь не был кабинетным учёным. Он находил время блистать в обществе, а его семейная жизнь дала Араго повод заметить, "что слава великих открытий иногда соединяется со спокойствием и счастьем".

Малюс

Не меньший интерес, хотя и в другом отношении, представляет биография другого участника великого спора, открытия которого заставили поколебаться автора принципа интерференции. Мы имеем в виду Малюса.

Этьен-Луи Малюс родился в Париже 23 июня 1775 г. в семье казначея. Малюс получил классическое образование и до конца жизни помнил наизусть обширные куски Иллиады, стихи Горация, Вергилия, Анакреона и других греческих и римских поэтов.

В 1793 г. Малюс выдержал экзамен в известную Мезьерскую инженерную школу. Окончить школу ему не пришлось вследствие происшедших в ней волнений. Волонтёром 15-го Парижского батальона Мал юс отправился в Дюнкерк, где участвовал в земляных фортификационных работах в качестве простого землекопа. Однако его способности быстро выдвинули его из простых рабочих, он рационализировал труд, и батальон, в котором работал Малюс, работал быстро с меньшей затратой труда. На это обратил внимание производитель работ инженер Лепер. Разговор Лепера с Малюсом имел то следствие, что Малюс попал в число первой полуторы тысячи учеников Политехнической школы (в числе этих учеников был, как мы помним, и Фурье).

По окончании школы 20 февраля 1796 г. Малюс отправился в Мец инженерным поручиком, затем в чине инженер-капитана принимал участие в военных операциях армии. Поведение Малюс а в военных кампаниях даёт возможность Араго сделать вывод, "что глубокие знания и гениальность в науке не ослабляют ни усердия, ни постоянства, ни мужества, ни предприимчивости - необходимых достоинств всякого хорошего офицера".

Затем Малюс участвовал в Мальтийской экспедиции. Из Мальты он был откомандирован в Египетскую армию, где был активным участником многих сражений и походов. Малюс был членом основанного Бонапартом Египетского института. В качестве инженера он строил фарт Дюпюи.

Потом Малюс был прикомандирован к дивизии Клебера, направлявшейся в Сирию. Он стоически переносит трудности похода в пустыне, активно содействует успеху осады и штурма Яффы, причём только случайно он избежал несчастья во время ночной вылазки неприятеля, захватившего брешь - батарею.

После взятия города в нём вспыхнула эпидемия чумы. Армия выступила в поход, Малюс получил приказание остаться с больными и ранеными солдатами. На 11-й день он заболел чумой. Заболели все его друзья, знакомые и, наконец, единственный слуга. Все они умерли. "Я остался один - без сил, без помощи, без друзей", вспоминал Малюс. Наконец его вывезли вместе с другими зачумлёнными на корабле в Лесбиехский лазарет.

Малюс рисует ужасную картину этого лагеря смерти. После месячного пребывания он был, наконец, изолирован от умирающих, выздоровел, был освобождён и вернулся к тяготам и опасностям Египетского похода. После перемирия с англичанами Малюс вернулся на родину и продолжал военно-инженерную службу, одновременно занимаясь и научными исследованиями по оптике. Он был членом Аркельского общества) а в 1810 г. был избран членом института.

За свои научные заслуги он получил от Королевского общества медаль Румфорда. Секретарь общества Юяг, извещая его об этом, писал: "Ваши опыты доказывают недостаточность моей теории, но не доказывают, что она ложная".

Ослабленный чумой и невзгодами военной жизни, организм Малюса не вынес. 23 февраля 1812 г. он умер от туберкулёза.

Таковы были эти два выдающихся деятеля, открытия которых дали толчок к возобновлению, после векового перерыва, дискуссии о природе света.

Уже в работе 1800 г. "Опыты и проблемы по звуку и свету" Юнг выдвигает новые аргументы против теории истечения:

1. трудность объяснения одинаковой скорости световых корпускул, выбрасываемых слабыми и сильными источниками,
2. трудность объяснения того обстоятельства, что при переходе из одной среды в другую одна часть лучей постоянно отражается, другая постоянно преломляется.

Особенно важна одна из акустических глав, где Юнг разбирает вопрос об интерференции водяных волн (термин принадлежит Юнгу) и показывает, что при наложении акустических волн могут возникать усиления и ослабления звука, комбинационные тоны и биения.

В бекеровской лекции, опубликованной Юнгом в "Phil. Trans." за 1801 г., уже сформулированы принципы волновой оптики. Вот эти принципы.

I. Светоносный эфир, в. высокой степени разрежённый и упругий, заполняет вселенную. II. Колебательные движения возбуждаются в этом эфире каждый раз, как тело начинает светиться. III. Ощущение различных цветов зависит от различной частоты колебаний, возбуждённых светом на сетчатке. IV. Все материальные тела притягивают эфирную среду, вследствие чего она накопляется в их веществе и на малом расстоянии вокруг них в состоянии большей плотности, но не большей упругости.

I. Все импульсы распространяются в однородной упругой среде с равной скоростью. II. Колебательное движение, которое по предположению происходит от колебания отдельной частицы, должно распространяться в однородной среде в форме сферы, но с различным количеством движения в различных частях. III. Часть сферического колебательного движения, пропущенная через отверстие в покоящуюся среду, будет попрежнему распространяться прямолинейно концентрическими поверхностями, оканчивающимися сбоку слабыми и нерегулярными частями вновь расходящихся колебательных движений.

IV. Когда колебательное движение достигает поверхности, являющейся границей раздела сред различных плотностей, имеет место частичное отражение, обязательно пропорциональное разности плотностей.

V. Когда колебательное движение проходит через поверхность, разграничивающую различные среды, оно идёт в таком направлении, что синусы углов падения и преломления находятся в постоянном отношении, равном отношению скоростей распространения в двух средах.

VI. Когда колебательное движение падает на поверхность менее плотной среды так косо, что оно не может быть правильно отражено, то оно полностью отражается под углом, равным углу его падения.

VII. Если предположить, что равноотстоящие колебательные движения проходят через среду, частицы которой способны совершать непрерывные колебания, несколько более медленные, чем упомянутые колебательные движения, то скорость последних будет уменьшена этой способностью к колебаниям и в той же среде тем больше, чем больше частота колебательных движений.

VIII. Когда два колебательных движения различного происхождения совпадают либо точно, либо весьма близко по направлению, то их совместное действие является комбинацией движений, принадлежащих каждому в отдельности.

Что же нового внёс Юнг в своих принципах после Гюйгенса? Относительно новыми являются вторая и третья гипотезы о световых колебаниях и связи света с частотой колебания. Мы говорим относительно, ибо до Юнга со всей отчётливостью эти гипотезы выдвинул Эйлер (см. гл. IX). Новой является четвёртая гипотеза об уплотнении эфира в весомых телах при сохранении упругости. Эта гипотеза в соединении с пятым предложением приводит к следующему выражению коэффициента преломления Пусть ε и σ - упругость и плотность чистого эфира, тогда скорость распространения упругого импульса, которым является свет, будет

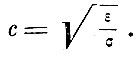
Для вещества упругость эфира попрежнему σ, плотность σ₁. Скорость света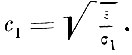

Показатель преломления по пятому предложению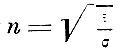

Этим выражением впоследствии воспользуется Френель, о чём мы будем иметь ещё случай сказать подробнее.

В положении III содержится принцип дифракции. Здесь Юнг делает новый шаг в развитии оптики Гюйгенса, который, как известно, полагал, что боковые волночки, идущие от краёв ограниченной волновой поверхности, физически не ощутимы и, следовательно, на экране края отверстия будут резко очерчены по законам геометрической оптики. Совершенно новым является предложение VIII, которое Юнг применяет к объяснению колец Ньютона. Здесь Юнг впервые сознательно измеряет длину световых волн и числа колебаний. Таким образом, основное понятие волновой оптики - длина волны - было введено Юнгом.

В следующей работе, напечатанной в "Phil. Trans." за 1801 г., Юнг формулирует открытый им "простой и общий закон". "Везде, где две части одного и того же света попадают в глаз различными путями, либо точно, либо весьма близко по направлению, свет становится более сильным там, где разность путей есть целое кратное некоторой длины, и наименее сильным в промежуточных состояниях интерферирующих частей; и эта длина различна для света различных цветов".

Так в оптике появляются термин интерференция (здесь ещё в форме причастия) и точная формулировка условий когерентности: интерферируют "две части одного и того же света".

В докладе 24 ноября 1803 г., опубликованном в "Phil. Trans." за 1804г., Юнг применяет свой принцип к объяснению дифракционных явлений. Дифракцию от нити Юнг объясняет интерференцией, причём полосы вне геометрической тени получаются интерференцией прямого света и света, отражённого от краёв; полосы внутри тени получаются вследствие интерференции пучков, дифрагированных краями нити. В центре геометрической тени получается светлая линия.

В этой же работе Юнг дополняет свою теорию цветов тонких пластинок указанием на потерю полуволны при отражении света от более плотной среды. Этим объясняется тёмное пятно в центре системы ньютоновых колец. Юнг проверил свою гипотезу опытом, налив между чечевицей из кронгласа и пластинкой из флинтгласа каплю сассафрасового масла (так что n₁<n₂<n₃) и убедился, что центральное пятно стало белым.

В той же работе Юнг стремится распространить принцип интерференции и на невидимые лучи. В отношении инфракрасных лучей это ему не удалось из-за отсутствия подходящих приёмников, но для ультрафиолетовых лучей опыт увенчался успехом. Юнг проектировал систему ньютоновых колец на бумагу, пропитанную раствором ляписа, и обнаружил три отчётливых тёмных кольца. Такова была первая форма спектрографа.

Свои опыты и принципы Юнг свёл в фундаментальную работу "Лекции по натуральной философии", вышедшей в 1807 г. Здесь Юнг описывает свой основной опыт интерференции от двух щелей, схема которого является основой расчёта аналогичных интерференционных опытов с интерференцией от двух когерентных источников. Однако Юнг не был уверен в успехе своей теории. Она либо игнорировалась, либо встречала резкую критику. Особенно яростно нападал на Юнга видный политический деятель и член Королевского общества Брум. Но дело было не только в этой критике. Появились новые факты, с которыми теория Юнга в её первоначальной форме не в силах была справиться.

Интерес к оптическим проблемам в начале XIX в. был вполне закономерным явлением. Если около двухсот лет назад этот интерес был продиктован потребностями мореплавания, то сейчас он стимулировался и развитием паротехники, и развитием химии, и развитием учения об электричестве. Казалось очень вероятным, что в природе тепла, света, электричества имеется что-то общее. Открытие фотохимических реакций, химические реакции, сопровождающиеся выделением тепла и света (в первую очередь горение), открытие тепловых и химических действий электричества,- всё это заставляло думать, что тщательное изучение природы света окажется не бесполезным и для решения важных практических и научных задач. Показательно обилие химических теорий света и электричества в духе ньютоновской корпускулярной теории (теория Гротгуса, Паррота и др.). Юнг связывал свои оптические воззрения с кинетической колебательной теорией тепла.

Рис. 193. Призма Рошона

Проблема стояла так: какова природа всех этих агентов - огня, света, электричества-флюидная или кинетическая? Специальный вопрос о природе света превращался, таким образом, в основную проблему физических воззрений.

Вместе с Юнгом реставрацию гюйгенсовских воззрений попытался произвести Волластон, указавший, что гюйгенсовское построение хорошо объясняет теорию двойного преломления. Но в 1807 г. Малюс представил Парижской академии мемуар о коэффициенте преломления непрозрачных тел, который, по мнению Лапласа, Гаюи и Гей-Люссака, был "математическим доказательством истины ньютонова учения".

Вскоре после этого 4 января 1808 г. Парижская академия предложила конкурсную задачу: "Составить поверенную опытом математическую теорию, двойного преломления света в различных кристаллических веществах". Срок конкурса был назначен на 1810 г.

12 декабря 1808 г. Малюс представил первые результаты своих опытов и основные принципы своей теории. Полная теория двойного преломления Малюса была напечатана в 1810 г. Следует отметить, что к началу XIX в. двойное преломление уже получило первое практическое применение. Астроном французского флота Рошон (1741-1817) сконструировал призму из исландского шпата, разделяющую обыкновенный и необыкновенный лучи, и применил её в своём микрометре (1801). Вполне понятно, что создание точной теории этого явления, теории, оправдывающейся опытом, было весьма актуальной задачей.

Размышляя над явлением, Малюс однажды вечером в конце 1808 г. посмотрел через кристалл исландского шпата на отражение заходящего солнца в стёклах Люксембургского дворца и к своему удивлению вместо двух изображений заметил одно. Проверяя своё открытие ночью, Малюс наблюдал отражение свечи в воде и заметил, что при отражении пучка под углом 36° к поверхности одно из изображений в кристалле исчезало. При других углах интенсивность обоих изображений вообще была различной, при вращении кристалла более интенсивное изображение ослабевало, а менее интенсивное делалось ярче.

Аналогичные явления наблюдались и для других отражающих поверхностей, только исчезновение одного из изображений происходило при других углах (для стекла при угле с поверхностью 35°). Правда, Малюс не установил точной зависимости этого угла от свойств поверхности и закон tgi = n был найден Брюстером в 1815 г.

Далее, Малюс изучал отражение обыкновенного и необыкновенного луча и нашёл, что если один луч отражается, то другой проходит во вторую среду. Все эти факты привели Малюса к выводу, что гипотеза Ньютона о наличии в световом луче "изначальных" качеств асимметрии весьма вероятна.

Полярные свойства частиц, так отчётливо проявляющиеся в электрохимических процессах, навели его на мысль предполагать в световом луче наличие таких же полярных свойств и ввести термин "поляризация света". Поляризованный свет Малюс анализировал сначала с помощью исландского шпата, а затем и зеркала. Этот опыт и дал ему возможность определить поляризованный луч, как такой "световой луч, который при одинаковом угле падения на прозрачное тело обладает свойством или быть отражённым, или же уклониться от отражения, обратившись к телу другой своей стороной; эти стороны или полюсы светового луча расположены всегда под прямым углом друг к другу". Малюс доказал, что обыкновенный и необыкновенный лучи поляризованы во взаимна перпендикулярных плоскостях, а в работе 1810 г. сформулировал закон интенсивности для поляризованного света, прошедшего через анализатор; она пропорциональна cos² α, где α - угол, образованный плоскостью поляризации с плоскостью главного сечения кристалла.

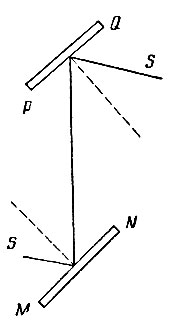
Рис. 194. Зеркала Малюса

Малюс показал, что двойное преломление с тем же характером поляризации, как и в исландском кристалле, получается и в ряде других кристаллов: аргоните, барите и т. д.

Далее, Малюс исследовал поляризацию при простом преломлении. Это же явление было одновременно открыто и Био. Свет при преломлении оказывается частично поляризованным, поляризация преломлённого света противоположна поляризации отражённого. Наконец, Малюс исследовал анизотропию кристаллических тел и органических веществ и нашёл, что все кристаллические вещества, за исключением тех, которые кристаллизуются кубами или правильными октаэдрами, обнаруживают оптическую анизотропию.

То же самое свойство было открыто им и в органических веществах.

Открытия Малюса послужили толчком к теоретическому и экспериментальному изучению двойного преломления. Исходя из концепции притягательного действия молекул тела на световые корпускулы и допустив, что в двоякопреломляющей среде это притягательное действие слагается из двух частей: одной, не зависящей от направления луча, и другой, зависящей от этого направления, Лаплас вывел формулу

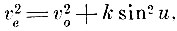
где v₀ - скорость обыкновенного луча, v_e - скорость необыкновенного луча и u - угол, образованный направлением необыкновенного луча с оптической осью, k - константа, зависящая от свойств среды. Для двуосных кристаллов Био нашёл

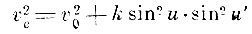
и показал, что k может быть как положительным, так и отрицательным, и таким образом кристаллы могут быть не только притягивающими, но и отталкивающими.

Араго, проверяя результаты Малюса, рассматривал отражённый свет через трубку Рошона и нашёл, что оба изображения окрашены в до-полнительные цвета (объектив трубки был изготовлен из горного хрусталя). Продолжая исследование, Араго наблюдал окрашивание слюдяных и гипсовых пластинок, помещённых между двумя отражающими поверхностями, параллельными друг другу и ориентированными к падающему пучку под углом полной поляризации. При повороте анализирующего зеркала цвет пластинки изменялся на дополнительный. То же самсе наблюдалось, если пластинка помещалась между двумя кристаллами исландского шпата. Араго установил, что цвет и характер явлений зависят от толщины пластинок.

Хроматическую поляризацию в сходящихся лучах описал в 1813 г. Брюстер (1781-1868). В одноосных кристаллах он описал цветные кольца с центральным крестом, а годом спустя - и хроматическую поляризацию в двухосных кристаллах.

Те же явления наблюдали Волластон в 1814 г., Био и Зибен в 1815 г. В том же 1815 г. Био установил законы явления вращения плоскости поляризации, которое впервые наблюдал в 1811 г. Араго в кварце.

Все эти явления чрезвычайно усложнили вопрос о природе света. Если открытие Малюса в своей первоначальной форме делало весьма вероятной гипотезу о полярных световых корпускулах и Юнг, как мы уже говорили, сильно поколебался в своих взглядах, то новые факты говорили об изменчивости полярных свойств светового луча.

Сам Араго появление цветов при помещении между скрещенными поляризатором и анализатором кристаллической пластинки приписал способности луча деполяризоваться. Био считал, что теория световых корпускул Ньютона должна быть дополнена теорией подвижной поляризации: ось поляризации совершает периодические колебания и с интервалом, пропорциональным интервалу световых приступов. Простые явления отражения и преломления света оказались до чрезвычайности усложнёнными. Вопрос о создании единой теории света, объясняющей как новые, так и уже давно известные факты, назрел.

Эта теория была создана инженером Огюстом Френелем. Френель родился 10 мая 1788 г. в Брольи, в Нормандии, в семье архитектора. В противоположность Юнгу, он не отличался в детстве блестящими способностями, к восьми годам он едва научился читать, но зато прослыл среди своих сверстников искуснейшим конструктором бузинных пушек и луков.

В 1801 г. Френель поступил в Центральную школу г. Кана. Затем Френель поступил в Политехническую школу (1804), где, несмотря на своё слабое здоровье, серьёзно мешавшее напряжённым занятиям в школе, своими способностями обратил на себя внимание Лежандра.

Из Политехнической школы Френель перешел в школу Путей сообщения. Получив звание инженера, Френель в течение восьми лет занимался дорожными работами в Вандее, Дроме и др. Во время реставрации Френель как роялист присоединился к войскам Бурбонов. Поэтому в период ста дней он был отставлен от должности. Это имело для него и свою хорошую сторону: во время вынужденного безделия он занялся вопросами оптики и в 1815 г. представил в Академию первое исследование о дифракции света. Окончательно разработанный труд по дифракции получил в 1819 г. премию академии. В 1823 г. Фронель был избран членом академии. Но в 1824 г. сильное кровотечение заставило его отказаться от всякой научной деятельности. Он умер 14 июля 1827 г.

Френель не знал о работах Юнга, когда приступил к изучению дифракционных явлений. Он исходил из принципа Гюйгенса, дополненного им принципом интерференции. Это дало ему возможность получить законы геометрической оптики: прямолинейное распространение света, геометрическое отражение и преломление. Все эти явления первоначальной теорией Гюйгенса объяснялись не вполне удовлетворительно. Френель показал, что законы геометрической оптики имеют место только при бес-конечно больших отражающих и преломляющих поверхностях и отверстиях. Если, например, размеры зеркальной поверхности становятся сравнимыми с длиной волны, то должна иметь место дифракция. Точно так же при малых размерах ширм и отверстий будет наблюдаться дифракция. Но в отличие от Юнга, полагавшего, что наружные полосы получаются интерференцией прямого пучка с лучами, отражёнными от краёв ширмы, Френель считает, что отражение от краёв не имеет места. Его расчёт основывается на учёте действия всех точек волнового фронта, не закрытых экраном. Разумеется, такое игнорирование действия краёв не может быть физически оправдано; но трудности строгой теории дифракционных явлений настолько велики, что только в 1895 г. Зоммерфельд разобрал простой случай дифракции от края экрана. Сам Френель дал приближённую теорию, но вполне охватывающую существенные черты явления.

Его приближённый способ подсчёта путём разбивания волнового фронта на зоны, которые так и вошли в учебники под названием зон Френеля, общеизвестен^*.

^* (Более точное вычисление интенсивности в какой-либо точке экрана приводит к выражениям, содержащим так называемые интегралы Френеля:

)

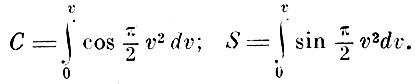
Френель приложил свою теорию к рассмотрению дифракции от края экрана и круглого отверстия. Результаты вычислений оказались в хорошем согласии с опытом. Это была первая количественная теория дифракционных полос, и Араго, рассматривавший вместе с Пуансо работу Френеля, сразу превратился в приверженца новой теории.

Но Пуассон вывел из формулы Френеля следствие, ускользнувшее от внимания автора, а именно, что в центре тени от круглого экрана должна быть такая же освещённость, как если бы никакой преграды для света не было. Араго настолько уверовал в силу теории Френеля, что не замедлил проверить это парадоксальное следствие опытом. Возражение Пуассона превратилось в свою прямую противоположность, опыт блестящим образом подтвердил следствие теории.

Этот факт произвёл огромное впечатление, хотя ещё в первой половине XVIII в. Делиль наблюдал в центре тени от круглого диска светлое пятнышко, да и Юнг уже указывал, что в центре тени от нити должна быть светлая полоска.

Как было указано выше, мемуар Френеля о дифракции был премирован Академией, хотя противники волновой теории далеко ещё не сложили оружия. Но согласовывать старую теорию с новыми фактами становилось всё более затруднительным. Особенно трудно было объяснить классический опыт Френеля с двумя зеркалами, где Френель чрезвычайно убедительно показал, как лучи света, идущие от двух одинаковых мнимых источников, попеременно погашают и усиливают друг друга. Но и перед волновой теорией стояли значительные трудности.

Предстояло применить принцип интерференции к явлениям хроматической поляризации. Юнг полагал, что цвета кристаллических пластинок объясняются интерференцией обыкновенного и необыкновенного лучей. Френель в 1816 г. занялся проверкой этого предположения и пришёл к отрицательному результату. Дальнейшие исследования, предпринятые им совместно с Араго, привели к установлению следующих законов интерференции поляризованных лучей:

I. При тех самых условиях, при которых два луча обыкновенного света как бы уничтожают друг друга^*, два луча, поляризованные в противоположных направлениях^**, не оказывают влияния друг на друга^***.

^* (Т. е. интерферируют.)

^** (Т. е. во взаимно перпендикулярных плоскостях.)

^*** (Не интерферируют.)

II. Два луча, поляризованные в одном и том же направлении, действуют друг на друга подобно обыкновенным лучам.

III. Два луча, поляризованные первоначально в противоположных направлениях, не интерферируют, если даже будут приведены в одну плоскость поляризации^*.

^* (Предполагается, что лучи произошли из естественного луча. См. IV закон.)

IV. Два луча, поляризованные в противоположных направлениях и затем приведённые к одной и той же поляризации, действуют друг на друга точно так же, как естественные лучи, если они возникли из луча, первоначально поляризованного в одном направлении.

Юнг уже после первых опытов Френеля сообщил в письме Араго от 12 января 1817 г., что для истолкования их результата (I закон) следует предположить, что световые колебания поперечны. Эта гипотеза не улыбалась ни самому Юнгу, ни Френелю, так как предположить существование упругости сдвига в такой тонкой жидкости, какой представлялся эфир, казалось, по меньшей мере, странным. Сам Френель говорит, что "эта гипотеза находилась в таком противоречии с общепринятыми представлениями о природе колебаний упругих жидкостей, что я долго не решался её принять; и даже когда совокупность всех фактов и долгое размышление убедили меня, что эта гипотеза необходима для объяснений оптических явлений, я пытался раньше, чем предоставить её на суд физиков, убедиться в том, что она не противоречит основам механики". Но эта гипотеза дала возможность Френелю не только истолковать при-ведённые выше законы интерференции поляризованных лучей, но и получить ряд других важных следствий. К ним относятся: теория вращения плоскости поляризации, теория отражения и преломления, теория двойного преломления.

Вращение плоскости поляризации Френель объяснил после того, как им был подробно исследован вопрос о сложении не интерферирующих взаимно перпендикулярных колебаний и установлено понятие об эллиптической и круговой поляризации. Допустив, что линейно-поляризованный луч разлагается в среде, вращающей плоскость поляризации, на два круговых с противоположными направлениями вращения, Френель выводит законы, найденные Био, в предположении, что оба компонента распространяются с разными скоростями. В правовращающем веществе скорость распространения кругового колебания, поляризованного вправо, больше, чем скорость левокругового колебания, и по выходе из вещества оба круговых колебания сложатся в линейное, плоскость поляризации которого будет повёрнута относительно первоначальной вправо на угол

Френель дал и изящное экспериментальное доказательство своей теории: пучок линейно-поляризованного света падает на основание призмы, сложенной из трёх призм: двух прямоугольных из правовращающего кварца и промежуточной тупоугольной с преломляющим углом в 152° из левовращающего кварца. Из призмы пучок выходит расщеплённым на два, поляризованных по кругу в противоположных направлениях. В своих опытах Френель располагал достаточными средствами для анализа круговой поляризации. Эти средства были найдены им при изучении поляризации при простом преломлении и отражении. Френелевская теория отражения и преломления основывалась не на вполне строгих предпосылках, но её выводы подтверждены и электромагнитной теорией света. Предпосылки теории Френеля следующие:

1. Свет - поперечные колебания в упругой среде, распространяющиеся со скоростью 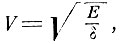где Е - упругость эфира, δ - его плотность.
2. При переходе из одной среды в другую упругость эфира не меняется, изменяется его плотность. Поэтому показатель преломления
   
   
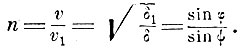
3. В пограничном слое алгебраическая сумма слагающих амплитуд, параллельных границам раздела падающей и отражённой волны, равна соответствующей компоненте амплитуды преломлённой волны.
4. Живая сила падающей волны в некотором объёме, ограниченном частью поверхности, на которую падает волна, и отрезками лучей, равна сумме живых сил отражённой и преломлённой волн, отходящих от той же части поверхности и прошедших пути соответственно общему времени распространения всех трёх волн.

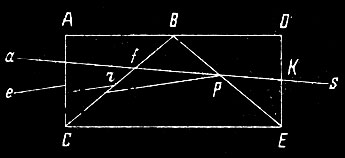
Рис. 195. Призма Френеля

Отсюда получаются знаменитые формулы Френеля:

а) Для составляющих амплитуд, параллельных границе раздела (плоскость поляризации параллельна плоскости падения),

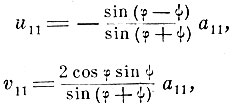
где u₁₁ - составляющая амплитуда отражённого луча, v₁₁ - составляющая амплитуда преломлённого луча, а₁₁ - составляющая амплитуда падающей волны.

в) Для составляющих амплитуд, параллельных плоскости падения (плоскость поляризации перпендикулярна плоскости падения),

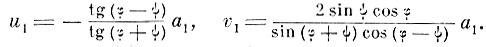
Из этих формул вытекает и закон Брюстера, и найденный Араго закон частичной поляризации отражённого и преломлённого луча (интенсивности поляризованных частей в отражённом и преломлённом лучах одинаковы). В формулах Френеля содержится и закон изменения фазы при отражении от более плотной среды (потеря полуволны). Но Френель пошёл дальше. Он пожелал исследовать случай полного отражения. С исключительной проницательностью Френель обобщил свои формулы и на случай sin φ>n,

положив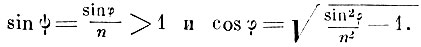

Тогда амплитуды отражённой волны будут представляться суммой действительной и мнимой части. Это различие, по Френелю, интерпретируется как разложение её на две части, из которых одна сдвинута по отношению к другой по фазе на ^π/₂.

В самом деле, если формально представить изменение фазы амплитуды на ^π/₂ умножением на коэффициент α, то изменение фазы на π должно представляться умножением на α², а так как при изменении фазы на π амплитуда меняет знак, то

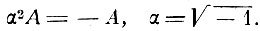
Но в таком случае формулы Френеля приводят к следующему результату: интенсивности обоих компонент отражённой волны оказываются равными соответствующим интенсивностям падающей волны (полное отражение), но фазы колебаний отражённой волны не совпадают с фазами упавшей волны. При этом скачок фазы для компоненты, параллельной отражающей поверхности, и для компоненты, параллельной плоскости падения, оказывается различным. Обе компоненты отражённой волны будут сдвинуты по фазе друг относительно друга на угол ε, определяемый равенством

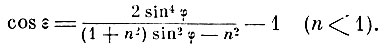
Если свет падает на стекло 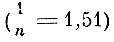под углом φ = 55°, то 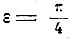при двух отражениях 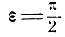На этом основано действие параллелепипеда

Френеля, позволяющего получить из линейно-поляризованного света свет, поляризованный по кругу, и наоборот. На грань призмы, продольное сечение которой параллелограмм с углом 55°, падает перпендикулярно к ней линейно-поляризованный луч, плоскость поляризации которого составляет угол 45° с плоскостью падения, так что обе компоненты амплитуды равны по величине. После двукратного полного отражения между компонентами создаётся разность фаз ^π/₂ и свет выйдет поляризованным по кругу. I

Рис. 196. Параллелепипед Френеля

Наконец, Френель рассмотрел вопрос о двойном преломлении в двухосных кристаллах (и как частный случай - одноосных кристаллах). Его теория зиждется на следующих предпосылках:

1. Плоскость световых колебаний перпендикулярна плоскости поляризации.
2. При распространении линейных поперечных колебаний в упругой среде в ней возникают упругие силы, совпадающие с точностью до постоянного множителя, не зависящего от направления распространения волны, супругой силой, возникающей при колебании одной частицы.
3. Когда в однородной среде распространяются плоские волны, то действуют только те составляющие упругих сил, которые параллельны плоскости волнового фронта.
4. Скорость плоской волны, распространяющейся в какой-либо однородной среде без изменения формы, пропорциональна квадратному корню из действующей упругой силы, вызванной колебаниями.

В анизотропной среде направление упругой силы, вызванной смещением колеблющейся частицы, не совпадает с направлением этого смещения, и только в том случае, когда направление колебания совпадает с направлением одной из трёх главных осей упругости, упругая сила будет параллельна смещению. Если значение коэффициентов упругости для трёх главных осей ox, oy, oz суть е₁, е₂, е₃, то коэффициент упругости для смещения направленного по r (cos α, cos β, cos γ)

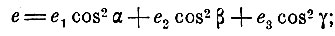
положив

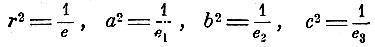
и

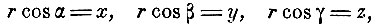
получим уравнение эллипсоида упругости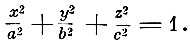 Длина радиуса-вектора этого эллипсоида определяет упругость среды в направлении радиуса-вектора. Главные скорости распространения волны

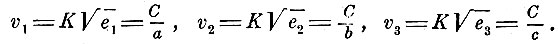
В соответствии с основными предпосылками получается простое геометрическое правило для определения скорости волн в анизотропной среде. Чтобы определить скорость волны, распространяющейся по какому-нибудь направлению ON, строим в точке О эллипсоид упругости и рассекаем его поверхность плоскостью, проходящею через центр О и перпендикулярной ON. Направления полуосей r₁ и r₂ эллипса, получившегося в плоскости сечения, определяют направление двух линейно-поляризованных колебаний, распространяющихся по данному направлению ON, а величины

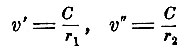
скорости распространения этих колебаний. Если провести из центра всевозможные направления и отложить вдоль этих направлений отрезки, пропорциональные соответствующим скоростям, то геометрическое место концов этих отрезков даст волновую поверхность.

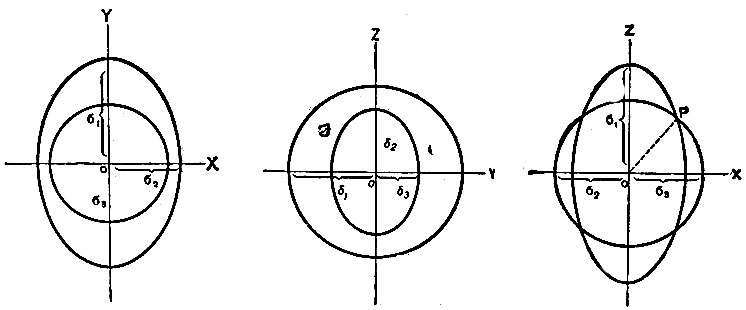
Рис. 197. a, b, c. Сечение волновой поверхности

Сечения этой поверхности координатными плоскостями хоу, yoz, zox имеют вид, изображенный на чертежах (197 а, b, с). Так как в трёхосном эллипсоиде существуют два направления, для которых нормальные к ним плоскости сечения, проходящие через центр, пересекают поверхность его по окружностям, то существуют две оси, вдоль которых волна распространяется с одной скоростью. Это - две оптические оси двуосного кристалла. В частности, если эллипсоид - эллипсоид вращения (а = b), то мы получаем одноосный кристалл, и волновая поверхность вырождается в поверхность Гюйгенса.

Френель

Построение Френеля показывает, что лучи не совпадают по направлению с нормалями к волновой поверхности. Поляризация и законы двойного лучепреломления описываются теорией Френеля правильно, хотя предпосылки её вызывают сомнения, да и строгого вывода уравнения волновой поверхности (поверхности четвёртого порядка) Френель не дал. Тем не менее уже сам Френель мог проверить важное следствие своей теории, а именно, что в двухосных кристаллах одна из волн подчиняется обычному закону преломления, если плоскость падения совпадает с главной плоскостью кристалла. Но ещё более важным следствием из теории Френеля было теоретически предсказанное Гамильтоном (1832) явление конической рефракции, открытое в соответствии с указаниями теории Ллойдом в следующем, 1833 г.

Этот тонкий эффект, связанный с формой волновой поверхности, чрезвычайно трудно получить экспериментально. Шустер рассказывает, что когда Максвелл получил кафедру экспериментальной физики, он с напряжением работал над воспроизведением опытов Ллойда. Как только эффект был получен, обрадованный Максвелл выбежал из лаборатории, ища, с кем бы поделиться радостью вознагражденного труда, встретив своего коллегу, профессора прикладной математики, он спросил его: "Хотите посмотреть коническую рефракцию?"- "Нет, благодарю Вас,- ответил тот,- я всю жизнь её преподавал и не хочу, чтобы моё представление о ней изменилось". Ответ, достойный Леверрье, не пожелавшего взглянуть на Нептуна, существование которого он установил вычислением. Недаром открытие конической рефракции сравнивалось с этим знаменитым астрономическим открытием.

Рис. 198. Луч и нормаль

Блестящие теоретические исследования Френеля не мешали ему решать и важные практические задачи. Он разработал лучшую, по условиям того времени, систему освещения маяков, заменив параболические зеркала ступенчатыми линзами Френеля (линзы этого типа использовались уже Бюффоном для концентрации тепловых лучей). Теория и практика гармонично сочетались в творчестве Френеля.

Упомянем ещё об одном следствии из теории Френеля. Предположение, что в веществе эфир сгущается, не меняя упругости, приводит его к выводу о частичном увлечении эфира движущимися телами. В самом деле, пусть некоторый брусок движется со скоростью v, причём плотность эфира в бруске δ₁, плотность чистого эфира δ. Вместе с движением бруска происходит и изменение плотности эфира, сгущённая часть эфира δ₁ - δ перемешается со скоростью v или весь эфир в бруске перемещается со скоростью v' = kv. Таким образом,

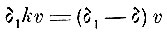
и

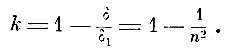
Открытия Френеля означали наступление нового этапа оптики - оптики упругого эфира. Ньютонианским воззрениям был нанесён мощный удар. Однако оставалась ещё область физики/где торжество ньютонианских концепций казалось обеспеченным. Но ив этой области наметился переворот, который вначале, казалось, вёл к торжеству ньютонианства, но, в конце концов, привёл к совершенно противоположному результату. Мы имеем в виду электродинамику.