Электрические измерения. Законы тока

Количественные теоретические исследования в электродинамике становились возможными благодаря успехам электрометрии. В развитии последней заслуги Вебера неоспоримы.

Прежде всего надо было выбрать единицы электрических величин. Развивая идеи Гаусса об абсолютной системе единиц, Вебер указывает на следующие возможности определения единицы силы тока.

Единица электричества может быть выбрана по примеру гауссовой единицы магнетизма из закона Кулона. Тогда единица силы тока может быть определена как сила тока, "который возникает, когда через каждое поперечное сечение цепи в единицу времени проходит единица свободного положительного электричества в одном направлении и столько же отрицательного в противоположном". Эту единицу, установленную им в 1855 г., Вебер назвал механической.

Ещё раньше, в первых исследованиях 1846 г., он указал на возможность определения трёх единиц силы тока: это, во-первых, электролитическая единица. В качестве такой единицы Вебер предлагает силу тока, который в 1 секунду разлагает 1 мг воды. Вторую единицу он предлагает определить из магнитных действий тока. Эта единица определяется, как сила такого тока, который, обтекая плоскость размером в единицу площади, действует на расстоянии совершенно также, как магнит, обладающий моментом, равным единице, ось которого перпендикулярна плоскости тока. Практически Вебер предлагает использовать для измерения тока в магнитных единицах тангенс-буссоль, принцип которой был предложен Пулье в 1837 г. и которую Вебер впервые применил в 1842 г. Единица силы тока, протекая по окружности буссоли, отклонит его на угол 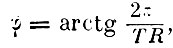где R - радиус буссоли, Т - горизонтальная составляющая земного магнетизма. В-третьих, единица тока может быть определена из динамических взаимодействий токов. Динамическая единица силы тока- это сила такого тока, который, протекая по элементу длины, равной единице, действует на равный ему параллельный элемент тока, по линии, перпендикулярной к ним, на расстоянии, равном единице, с силой в одну механическую единицу. В качестве примера укажем, что приведённый Нейманом "потенциал" двух токов

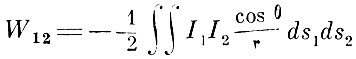
предполагает, что силы токов выражены в электродинамических единицах. Если бы они были выражены в механических единицах, то

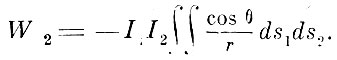
Отсюда видно, что магнитная единица в 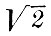больше динамической. Это было подтверждено Вебером. Он же нашёл, что магнитная единица в 106 ²/₃ раза меньше электролитической.

Особенно важным в историческом отношении было произведённое Вебером совместно с Кольраушем в 1856 г. сравнение магнитной единицы с механической. Опыт заключался в следующем. Лейденская банка С заряжалась определённым количеством электричества (это количество электричества могло быть измерено с помощью кулоновских весов). Банка разряжалась через тангенс-гальванометр в течение известного промежутка времени τ. По отклонению со можно было определить силу тока в магнитных единицах, которая, с другой стороны, равнялась ^e/_τ, где е - количество электричества, измеренное в механических единицах.

Из многочисленных измерений Вебер и Кольрауш нашли, что механическая единица относится к магнитной, как 1:155370*10⁶, а следовательно, к электродинамической, как 1*109860*10⁶ и к электролитической, как 1:16573*10⁶.

Отсюда можно было определить постоянную С в законе Вебера. Она оказалась равной

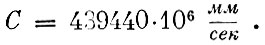
Эта величина равна скорости света в пустоте, разделённой на 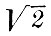. Этот важный факт авторами эксперимента был оставлен без внимания.

Продолжая развивать свою систему единиц, Вебер предложил в качестве единицы электродвижущей силы выбрать электродвижущую силу, которая индуцируется в витке проволоки, охватывающей площадь, равную единице, при повороте последнего из положения, параллельного магнитному полю силой в единицу, на угол 90° в течение одной секунды. Тогда абсолютная единица сопротивления оказывалась равной сопротивлению такого проводника, в котором единица электродвижущей силы создаёт ток, равный единице. Она имела размерность скорости и обозначалась ^мм/_сек.

Предложенная Вебером система, удобная в теоретических расчётах, на практике представляла значительные неудобства. Измерение электродвижущей силы путём сравнения с электродвижущей силой, полученной индукционным толчком, провести было невозможно. Практика выработала методы сравнения электродвижущей силы постоянно действующих источников и методы сравнения сопротивлений, которые позволяли, выбрав электродвижущую силу определённого источника за эталон, выражать все электродвижущие силы в этом масштабе.

Метод измерения электродвижущих сил был предложен в 1841 г.- Поггендорфом под названием метода компенсации.

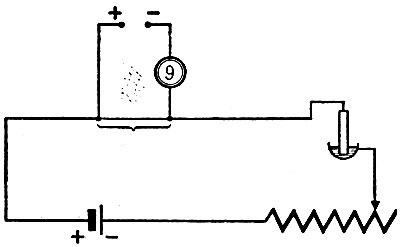
Рис. 234. Метод Поггендорфа

Чтобы измерить величину электродвижущей силы Е_х неизвестного источника, составляют цепь с вспомогательным источником Е₁>Е_х и известным сопротивлением r. Измеряемый источник включают навстречу источнику Е₁, и в его цепь включается чувствительный гальваноскоп. Регулируя реостатом силу тока i, которую можно измерить, например, серебряным вольтаметром, добиваются, чтобы гальваноскоп стал на нуль. Тогда Е_х = ir. В дальнейшем (1855) Боша применил этот метод для непосредственного сравнения электродвижущих сил с нормальным эталоном электродвижущей силы. Вспомогательный источник включён в цепь, составленную из проволоки (реохорда) и сопротивления. От подвижных контактов реохорда идёт измерительная цепь с гальванометром, в которую посредством коммутатора может быть включён либо нормальный эталон электродвижущей силы, либо испытуемый источник Е_х. Если установка на нуль в гальванометре осуществляется для цепи с Е_n при расстоянии между движками l₁, а установка на нуль для цепи с Е_х при расстоянии l₂, то

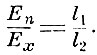
К этому времени были уже известны достаточно устойчивые (деполяризационные) гальванические элементы. Первым устроил постоянный элемент в 1829 г. А. Беккерель. Затем, в 1836 г., устроил свой известный элементе двумя жидкостями Даниэль. Этот элемент благодаря простоте устройства и достаточной надёжности (он сохранился и поныне в школьной практике) был в большом ходу. До изобретения "нормальных" элементов (Кларк, 1872) элемент Даниэля служил эталоном, и единица электродвижущей силы "Даниэль" была в ходу в конце прошлого века.

Элемент Грове (1839) давал в 1,5 раза большую электродвижущую силу, чем элемент Даниэля. Это также элемент с двумя жидкостями, H₂SO₄ и HNO₃. Электроды: платина в растворе HNO₃ и цинк в растворе H₂SO₄.

Бунзен в 1841 г. заменил дорогостоящую платину прессованным углем. Батареи Бунзена и Грове вплоть до изобретения динамомашины были главнейшими источниками электричества. Понятно, что электроэнергия была не дешева. Для слабых токов (в телеграфии) применялись в шестидесятых годах элементы Мейдингера, изобретённые в 1859 г.

В 1844 г. Ч. Уитстон (вначале музыкальный мастер, а затем профессор физики) предложил известную под названием "мостика Уитстона" схему для измерения сопротивлений. Эта схема позволяла, имея соответствующие эталоны, определять неизвестное сопротивление. Формулу для расчёта сопротивления по этому методу

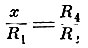
вывел Поггендорф и вместе с В. Вебером экспериментально проверил её правильность. Уитстон предложил в качестве эталона сопротивления медную проволоку длиной в 1 фут и весом 100 гран (6,5 г).

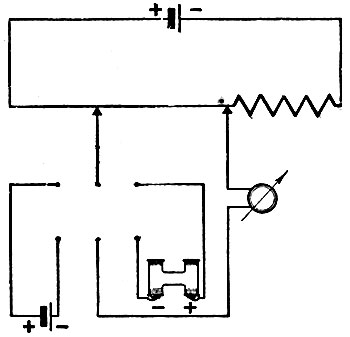
Рис. 235. Схема Боша

Русский физик Якоби изготовил и разослал по физическим лабораториям эталон в виде медной проволоки длиной 25 футов (7,62 м) и толщиной ²/₃ мм, весом 22449,3 мг. Вебер измерил этот эталон в абсолютной мере. Индуктор, состоящий из проволочной прямоугольной рамки, обмотанной тонкой проволокой, подвешен в магнитном поле Земли так, что рамка может вращаться около вертикальной оси, лежащей в средней плоскости её обмотки. Концы обмотки соединены с гальванометром.

Вначале определяется сопротивление R₀ индуктора и гальванометра. С этой целью рамка устанавливается в плоскости, перпендикулярной плоскости магнитного меридиана, и затем поворачивается на 180°. При этом в ней индуцируется электродвижущая сила

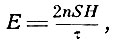
где τ - время поворота, Н - горизонтальная составляющая магнитного поля, n - число витков, S - площадь рамки. При этом в цепи пробегает ток

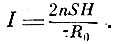
За время поворота τ пробежит количество электричества

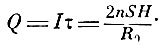
Подвижная часть гальванометра Вебера (магнит) обладала достаточно большим моментом инерции и, следовательно, большим периодом колебания по сравнению с промежутком времени τ. В таких условиях гальванометр работает как баллистический, и первый отброс α пропорционален Q*Q = сα, откуда

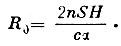
Этим способом Вебер и определил в 1852 г. сопротивление эталона Якоби в его магнитных абсолютных единицах. Оно оказалось равным 598*10⁷ (0,551 ома).

Эталон Якоби долго использовался в качестве единицы,но в конце концов выяснилось, что медь не обладает необходимым постоянством. Поэтому французские физики Пулье, Мари-Дэви и Делярив предложили ртуть. Вернер Симменс в 1860 г. предложил ртутный эталон в виде ртутного столба длиной 1 м и поперечным сечением в 1 мм² при 0° С (единица Симменса). В 1861 г. Британская ассоциация и Королевское общество учредили специальную комиссию во главе с В. Том юном для разработки вопроса о единицах. Однако в рассматриваемый нами период вопрос ещё разрешения не получил.

Из изложенного выше нетрудно усмотреть, что практические измерительные схемы (Поггендорфа, Уитстона) уже требовали знания законов разветвления токов. Частные случаи этой проблемы рассматривали и сам Ом и Уитстон, Погтендорф, Вебер, Пулье. В общем виде эта проблема была поставлена и решена студентом Г. Кирхгофом в 1845 г., когда будущему известному физику был всего 21 год.

Законы распределения токов в сложных цепях Кирхгоф дал в виде прибавления к работе "О прохождении тока через плоскость, в частности - ограниченную окружностью". Законы Кирхгофа гласят:

"Если через систему проводов, связанных между собою произвольным образом, проходят гальванические токи, то:

1. в случае, если провода 1,2... v сходятся в одной точке
   
   
   где I₁, I₂,.. I_v обозначают силы токов, проходящих по соответствующим проводам, причём все токи, направленные к упомянутой точке, являются положительными;
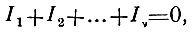
2. в случае, если провода 1,2... v образуют замкнутую фигуру,
   
   
   равно сумме всех электродвижущих сил, образующихся на пути 1, 2... v, где W₁, W₂... W_v обозначают сопротивления проводов I₁, I₂,.. I_v силы протекающих по ним токов, причём токи, текущие в одном направлении, считаются положительными".

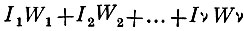
В работе 1847 г. Кирхгоф дал вывод своих уравнений и общее решение задачи о разветвлении токов. Это решение гласит:

"Пусть m представляет общее число точек пересечения, т. е. точек встречи двух или большего числа проводов, и пусть μ = n - m + 1 тогда общим знаменателем для всех величин Ш будет сумма тех сочетаний из W₁, W₂, ..., W_n по μ элементов в каждом, W_k1, W_k2,..., W_kμ, которые обладают тем свойством, что по удалении проволок k₁, k₂,..., k_μ не остаётся ни одной замкнутой фигуры; а числителем для Iv является сумма сочетаний из W₁, W₂, ..., W_n по μ-1 в каждом, W_k1, W_k2,..., W_kμ-1, имеющих то свойство, что по удалении проводов k₁, k₂, ..., k_μ-1 остаётся замкнутая фигура, заключающая в себе λ-й провод; каждое из этих сочетаний помножается на сумму электродвижущих сил, находящихся на соответствующей замкнутой фигуре. При этом электродвижущие силы следует считать положительными в том направлении, в котором I считается положительным". (Здесь n - общее число связанных проводов, W₁, W₂, ..., W_n - соответственно сопротивления этих проводов.)

Поясним правило Кирхгофа простым примером. Представим себе цепь, содержащую главную ветвь с источником Е и три параллельно соединённых проводника, сопротивления которых равны соответственно W₁, W₂, W₃. Сопротивление главной ветви обозначим W₄. Таким образом, в нашем примере n = 4, m = 2 (две узловые точки а и b).

Поэтому μ = n - m + 1 = 3, μ - 1 = 2. Знаменатель будет содержать сочетания из W₁, W₂, W₃, W₄ по 3, числитель по 2.

Якоби

Чтобы составить знаменатель, надо составить произведения из сопротивлений трёх проводов, таких, чтобы по их удалении не оставалось: ни одной замкнутой фигуры. Это будут W₁W₂W₃, W₁W₂W₄, W₂W₃W₄, W₁W₃W₄. Других сочетаний нет. Для составления I_v надо образовать одну замкнутую фигуру, удаляя два остальных провода так, чтобы в фигуру входил 1-й провод. Для тока I₁ это можно сделать единственным образом, удаляя сопротивления W₂ и W₃. В оставшемся контуре будет Е. Таким образом, числитель для тока I₁ будет EW₂W₃.

Для тока I₂ числитель будет ЕW₁W₃, для I₃ он равен ЕW₁W₂. Для I₄ провод R можно сохранить в замкнутом контуре тремя способами: удаляя W₁W₂, удаляя W₁W₃, удаляя W₂W₃. Поэтому числитель для тока I₄ будет Е (W₁W₂ + W₁W₃ + W₂W₃). Выражения для токов будут

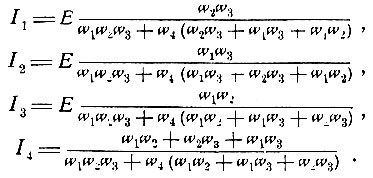
Нетрудно убедиться проверкой, что I₄ = I₁ + I₂ + I₃. Обратим внимание, что правила Кирхгофа выражают факт стационарности токов. Первый закон требует непременной замкнутости цепи постоянного тока.

Ток в любой точке линейной цепи (а в законах Кирхгофа речь идёт о линейных проводниках) не может создать накопления электричества. Второй закон означает, что потенциалы всех точек в установившемся процессе постоянны. Поэтому изменение режима в любом участке разветвлённой цепи вызовет соответствующие изменения во всех остальных участках, так, чтобы законы Кирхгофа вновь были удовлетворены.