
Теория Лоренца
Переходим к рассмотрению основных результатов Г. Лоренца. Лоренц предполагает, что состояние эфира вблизи наэлектризованных и намагниченных тел описывается двумя векторами 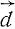 и
и 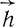 . В "чистом" эфире вектор
. В "чистом" эфире вектор 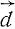 удовлетворяет уравнению
удовлетворяет уравнению
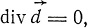
которое внутри заряженных тел переходит в уравнение
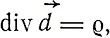
(I)
где  - объемная плотность электрического заряда. Вектор
- объемная плотность электрического заряда. Вектор 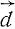 Лоренц называет "диэлектрическим смещением" и рассматривает как некое "смещение" в эфире, обусловленное электрическими зарядами. Другой характеристикой поля является "магнитная сила"
Лоренц называет "диэлектрическим смещением" и рассматривает как некое "смещение" в эфире, обусловленное электрическими зарядами. Другой характеристикой поля является "магнитная сила" 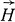 . Вектор магнитной силы удовлетворяет уравнениям:
. Вектор магнитной силы удовлетворяет уравнениям:
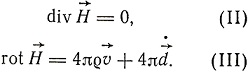
Здесь 
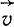 - плотность конвекционного тока движущихся зарядов,
- плотность конвекционного тока движущихся зарядов, 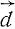 - плотность тока смещения в эфире. Четвертое уравнение теории имеет вид
- плотность тока смещения в эфире. Четвертое уравнение теории имеет вид
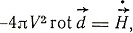
(IV)
где V - скорость света в эфире.

Г. А. Лоренц
Далее Лоренц вводит "электрическую силу", действующую на единицу заряда:
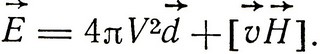
(V)
Эта сила в физике получила название "силы Лоренца". Лоренц выводит затем закон сохранения энергии для электромагнитного поля, причем полю приписывается энергия:
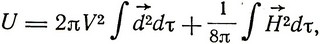
и вводится вектор Пойнтинга, характеризующий поток энергии через единичную площадку:
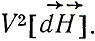
Очень важно отметить, что Лоренц (и также Лармор) обращает особое внимание на свойства симметрии уравнений поля. Первый раздел книги Лоренца заканчивается параграфом, носящим название "Обратимость движений и зеркальное изображение движения". Здесь он пишет: "Пусть дана система движущихся ионов и описывающие ее величины  1,
1, 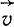 1,
1, 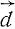 1 и
1 и 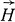 1. Соответствующие величины для второй системы мы обозначим через
1. Соответствующие величины для второй системы мы обозначим через  2,
2, 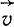 2,
2, 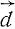 2 и
2 и 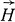 2, причем представим себе, что в некоторой произвольной точке эти величины в момент времени t совпадают с величинами
2, причем представим себе, что в некоторой произвольной точке эти величины в момент времени t совпадают с величинами  1, -
1, -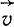 1,
1, 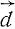 1 и
1 и 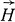 1 для времени -t".
1 для времени -t".
"Легко видеть, что в отношении  2 и
2 и 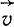 2 этому условию будет удовлетворять действительное движение ионов ... другими словами, движение ионов во второй системе получают, если обратить первоначальные заданные движения".
2 этому условию будет удовлетворять действительное движение ионов ... другими словами, движение ионов во второй системе получают, если обратить первоначальные заданные движения".
"Так как, далее, 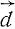 2 и
2 и 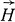 2 удовлетворяют условиям (I), (II), (III) и (IV), то состояние эфира, определяемое этими векторами, совместимо с движениями ионов".
2 удовлетворяют условиям (I), (II), (III) и (IV), то состояние эфира, определяемое этими векторами, совместимо с движениями ионов".
"Наконец, из уравнения (V) следует, что во второй системе силы, оказываемые в момент времени +t посредством эфира на ионы, имеют те же величины и направления, как соответствующие силы в первой системе в момент времени -t. Пусть также и остальные действующие на ионы силы в обоих случаях - в упомянутые моменты времени - тождественны, тогда можно заключить, что в этом отношении второе состояние движения может быть реализовано.
Посредством аналогичных соображений можно доказать возможность движения, являющегося "зеркальным изображением" данного в некоторой неподвижной плоскости.
Обозначим через Р2 зеркальное изображение точки P1 и обозначим величины в обоих системах - а именно для первой в P1 и для второй в Р2 - через  1,
1, 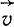 1,
1, 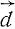 1,
1, 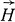 1 и
1 и  2,
2, 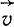 2,
2, 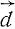 2,
2, 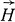 2. При этом пусть все время
2. При этом пусть все время  1=
1= 2 и векторы
2 и векторы 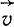 2,
2, 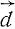 2,
2, 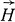 2 являются зеркальными изображениями векторов
2 являются зеркальными изображениями векторов 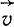 1,
1, 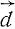 1 и -
1 и -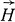 1. То, что второе состояние движения можно назвать зеркальным отражением первого, не требует пояснений".
1. То, что второе состояние движения можно назвать зеркальным отражением первого, не требует пояснений".
Лармор анализирует эти соотношения более подробно и, как было сказано, вводит понятие спиральное™ среды. Он определяет инвариантность системы по отношению к преобразованию времени, заключающемуся в изменении знака как ее обратимость. Консервативная система обратима, поскольку знак функции Лагранжа Т-U остается при таком преобразовании неизменным. Более сложно обстоит дело для механической системы с циклическими координатами, не входящими явно в выражение энергии. В частности, такие системы Гельмгольц рассматривал как механическую модель необратимых термодинамических процессов. Преобразование отражения заключается в изменении знака координаты х при сохранении знака времени. Тогда движение изменяется в свое зеркальное отражение в зеркальной плоскости yz. Так как при таком отражении правостороннее вращение вокруг оси х изменяется в левостороннее, и если отраженное движение может существовать так же, как и отражаемое, то среда не обладает спиральностью по отношению к оси х. Лармор заключает отсюда, что поведение физической системы при таком преобразовании может служить ключом к ее динамическим свойствам.
Вернемся к работе Лоренца. Второй раздел этой работы посвящен электродинамике движущихся сред. Он озаглавлен "Электрические явления в весомых телах, перемещающихся с постоянной скоростью через неподвижный эфир". Эту постоянную скорость Лоренц обозначает 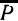 (отметим, что Лоренц обозначает всюду векторы жирным готическим шрифтом, который мы всюду заменяем на латинский).
(отметим, что Лоренц обозначает всюду векторы жирным готическим шрифтом, который мы всюду заменяем на латинский).
Для описания явлений в движущихся телах Лоренц вводит систему координат, жестко связанную с движущимся телом. Координаты точки относительно неподвижной системы (т. е. системы, связанной с покоящимся эфиром) Лоренц обозначает x, y, z. Координаты точки относительно системы, движущейся с телом, Лоренц называет относительными и обозначает (x), (y), (z). Точка будет считаться неподвижной, если она занимает неизменное положение относительно этой движущейся с телом системы координат, другими словами, понятия "покой" и "движение" рассматриваются в отношении этой "сопровождающей" системы координат и, таким образом, являются относительным покоем или относительным движением частиц в весомой материи. Если скорость такого относительного движения 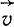 , то скорость частицы относительно эфира, которую Лоренц называет действительной скоростью, будет
, то скорость частицы относительно эфира, которую Лоренц называет действительной скоростью, будет 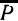 +
+ 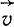 . Вместо производных по x, y, z, t Лоренц для описания явлений в движущихся телах вводит производные по (x), (y), (z) и t. При этом
. Вместо производных по x, y, z, t Лоренц для описания явлений в движущихся телах вводит производные по (x), (y), (z) и t. При этом 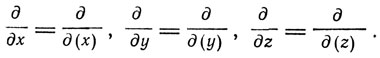 Что же касается производных по времени, то между производной по времени в сопровождающей системе, которую Лоренц обозначает ∂/∂t, и производной по времени в неподвижной системе, которую он обозначает
Что же касается производных по времени, то между производной по времени в сопровождающей системе, которую Лоренц обозначает ∂/∂t, и производной по времени в неподвижной системе, которую он обозначает 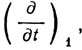 существует соотношение
существует соотношение
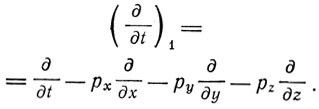
Таким образом, основные уравнения, отнесенные к системе осей, движущихся вместе с весомой материей, будут иметь вид
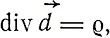 (I a)
(I a)полный ток
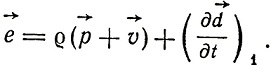
Далее
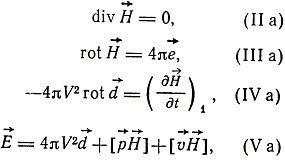
Эти уравнения могут быть приведены к виду
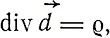 (I b)
(I b)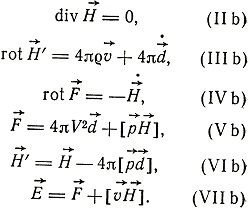
Из этих уравнений следуют формулы, содержащие каждая или только  , или только
, или только 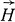 :
:
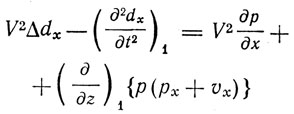
(A)
и т. д.
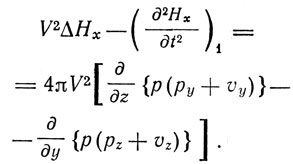
(B)
и т. д.
С помощью этих уравнений Лоренц рассматривает электрические явления в движущихся телах, в частности находит закон преобразования поля и плотности заряда для движущей заряженной частицы. Оказывается, что при движении такая частица должна деформироваться в направлении движения и шарообразное заряженное тело сплющивается в эллипсоид.
Законы электродинамики, найденные Лоренцем для движущихся сред, показывают, что распределение зарядов и силы, действующие между заряженными телами, будут изменяться при движении системы. "Однако это влияние,- пишет Лоренц,- ограничивается членами второго порядка, если считать дробь p/V величиной первого порядка". С точностью до первого порядка величины p/V все электрические и магнитные явления в движущихся телах происходят так же, как в покоящихся.
Начиная с третьего раздела своей работы Лоренц переходит к исследованию оптических явлений в движущихся телах. При этом он делает важный шаг, вводя вместо переменной t новую переменную
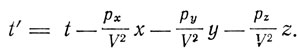
"Эту переменную t' можно рассматривать как время, отсчитываемое от некоторого момента, зависящего от положения рассматриваемой точки. Поэтому эту переменную можно назвать местным временем этой точки, в противоположность общему времени t".
В среде вместо величин  ,
, 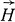 вводятся их усредненные значения. Вводится также новый вектор
вводятся их усредненные значения. Вводится также новый вектор 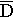 . Вектор
. Вектор 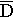 определяется уравнением
определяется уравнением
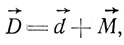
где 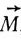 - электрический момент единицы объема и назван Лоренцем диэлектрической поляризацией. Он, как указывает Лоренц, совпадает с величиной, названной Максвеллом диэлектрическим смещением. В чистом эфире
- электрический момент единицы объема и назван Лоренцем диэлектрической поляризацией. Он, как указывает Лоренц, совпадает с величиной, названной Максвеллом диэлектрическим смещением. В чистом эфире 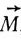 = 0 и
= 0 и 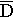 =
=  . В незаряженном диэлектрике
. В незаряженном диэлектрике
div 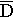 = 0(I)
= 0(I)
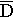 = 0(I)
= 0(I)
В движущихся телах вместо 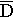 вводится вектор
вводится вектор 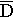 ' посредством уравнения
' посредством уравнения
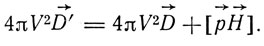
Если ввести местное время t', то величины, описывающие электромагнитные явления, будут функциями x, y, z и t Производные в движущейся системе обозначаются через
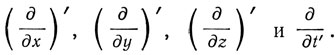
При этом
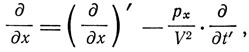
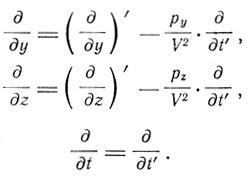
Под div' 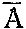 будем понимать выражение
будем понимать выражение
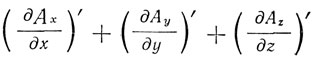
и под rot'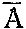 - вектор с компонентами
- вектор с компонентами
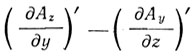
и т. д.

А. Майкельсон
Уравнения поля в неподвижной среде по Лоренцу имели вид:
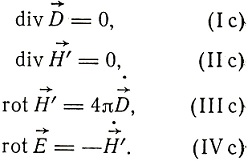
При этом в изотропной среде
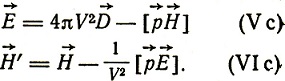
Если для движущихся тел ввести величины t' и 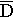 ' и пренебречь членами второго порядка, то уравнения поля будут иметь вид:
' и пренебречь членами второго порядка, то уравнения поля будут иметь вид:
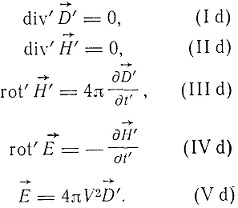
Как видим, эти уравнения имеют тот же вид, что и уравнения для покоящейся среды. Это совпадение, как пишет Лоренц, "открывает путь для простого решения проблемы влияния движения земли на оптические явления".
"Именно, если для системы покоящихся тел известно состояние движения, для которого
Dx, Dy, Dz, Ex, Ey, Ez, Hx, Hy, Hz
являются определенными функциями x, y, z и t, то в той же системе, когда она перемещается со скоростью 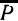 , может существовать состояние движения, для которого
, может существовать состояние движения, для которого
D'x, D'y, D'z, Ex, Ey, Ez, H'x, H'y, H'z
будут такими же функциями x', y', z' и t'". Этот результат Лоренц применяет к ряду оптических явлений. Так, если в покоящейся системе величины 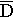 ,
, 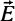 и
и 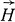 являются периодическими функциями t с периодом Т, то величины
являются периодическими функциями t с периодом Т, то величины 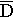 ',
', 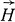 ',
', 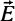 будут периодическими функциями t', а следовательно, и t при постоянных x, y, z.
будут периодическими функциями t', а следовательно, и t при постоянных x, y, z.
При этом следует отличать абсолютный и относительный периоды, первый соответствует точке, покоящейся в эфире, второй - точке, покоящейся относительно движущегося тела. Значит, если состоянию колебаний в движущейся системе соответствует состояние колебаний в покоящейся системе, то относительный период колебаний в первом случае должен совпадать с периодом колебаний во втором случае.
Далее, если в покоящейся системе в каком-либо месте 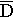 ,
, 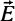 ,
, 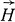 обращаются в нуль, то в соответствующем месте движущейся системы
обращаются в нуль, то в соответствующем месте движущейся системы 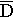 ',
', 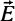 ,
, 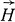 ' также обращаются в нуль. Отсюда следует, что поверхность образующихся в покоящихся телах границ пространства, заполненного светом, будет иметь такое же значение в движущихся телах. Если, например, в покоящейся однородной среде цилиндрическая поверхность ограничивает пучок света, то и в движущейся системе существует такой же пучок. Образующие линии этой цилиндрической поверхности называются световыми лучами, а в случае движения - относительными световыми лучами. В движущейся системе относительные световые лучи относительного периода Т будут отражаться и преломляться по тем же законам, как и лучи периода Т в покоящейся системе. Далее, если в покоящейся системе наблюдаются интерференционные и дифракционные явления, то появляющиеся при этом темные полосы остаются такими же в точно тех же местах для соответствующего состояния движущейся системы. "Вообще,- пишет Лоренц,- по нашей теории движение земли не оказывает в первом порядке никакого влияния на опыты с земными источниками света".
' также обращаются в нуль. Отсюда следует, что поверхность образующихся в покоящихся телах границ пространства, заполненного светом, будет иметь такое же значение в движущихся телах. Если, например, в покоящейся однородной среде цилиндрическая поверхность ограничивает пучок света, то и в движущейся системе существует такой же пучок. Образующие линии этой цилиндрической поверхности называются световыми лучами, а в случае движения - относительными световыми лучами. В движущейся системе относительные световые лучи относительного периода Т будут отражаться и преломляться по тем же законам, как и лучи периода Т в покоящейся системе. Далее, если в покоящейся системе наблюдаются интерференционные и дифракционные явления, то появляющиеся при этом темные полосы остаются такими же в точно тех же местах для соответствующего состояния движущейся системы. "Вообще,- пишет Лоренц,- по нашей теории движение земли не оказывает в первом порядке никакого влияния на опыты с земными источниками света".
Этот принцип относительности первого порядка объясняет целый ряд известных оптических фактов. Вместе с тем гипотеза неподвижного эфира позволила Лоренцу дать объяснение таким явлениям аберрации света и опыту Физо с движущейся водой.
Кажущееся "увлечение эфира" в этом случае он объяснил движением заряженных частиц через неподвижный эфир и рассчитал отсюда коэффициент Френеля.
Но теперь возникает вопрос: а как быть с эффектами второго порядка? Ко времени выхода "Опыта" были уже известны результаты знаменитого опыта А. Майкельсона, в котором должны были обнаружиться эффекты второго порядка. Как известно, эти опыты, повторенные уже два раза (в 1881 и 1887 гг.)", не дали ожидаемого эффекта. В шестом разделе своей работы Лоренц oписывает как опыт Майкельсона 1881 г., так и опыт Майкельсона и Морли 1887 г. При этом он ссылается на свою работу 1892 г., в которой он для объяснения отрицательного результата опыта Майкельсона выдвинул гипотезу продольного сокращения размеров тел вследствие движения. При этом он указывает, что Фитцджеральд сообщил ему лично, что аналогичная гипотеза была уже выдвинута им раньше в его лекциях. О гипотезе Фитцджеральда сообщил печатно Лодж в статье "Проблема аберрации", опубликованной в 1893 г. Так или иначе, Лоренц узнал о гипотезе Фитцджеральда только после того, как он уже опубликовал аналогичную гипотезу. В своем "Опыте" он излагает существо этой гипотезы следующим образом:
"§ 91. Как ни удивительной может показаться на первый взгляд эта гипотеза (о сокращении размеров тел при движении.- П. К.), можно все же согласиться, что она не столь уж странная, коль скоро примем, что молекулярные силы так же, как мы это сейчас определенно утверждаем об электрических и магнитных силах, действуют посредством эфира. Если это так, то весьма вероятно, что перемещение изменяет действие между двумя молекулами таким же образом, как оно изменяет притяжение или отталкивание между заряженными частицами. Так как форма и размеры твердых тел будут в последней инстанции обусловлены интенсивностью молекулярных действий, то в этом случае должно происходить изменение размеров".
"В теоретическом отношении, таким образом, нельзя ничего возразить против этой гипотезы. Что касается ее экспериментального исследования, то прежде всего следует заметить, что речь идет об исключительно малых удлинениях и сокращениях ... Сокращение диаметра Земли составляет около 6,5 сантиметров ..." Лоренц далее показывает, что к такому же результату можно прийти, если допустить, что к молекулярным системам S1 и S2, из которых вторая покоится, а первая движется со скоростью 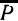 вдоль оси x, применить результаты, найденные им для электростатических систем, состоящих из заряженных частиц. Для таких электростатических систем Лоренц нашел, что координаты точки x, y, z в системе S1 и соответствующие координаты x', y', z' той же точки в системе Е'x, Е'y, Е'z в S2 соотношениями
вдоль оси x, применить результаты, найденные им для электростатических систем, состоящих из заряженных частиц. Для таких электростатических систем Лоренц нашел, что координаты точки x, y, z в системе S1 и соответствующие координаты x', y', z' той же точки в системе Е'x, Е'y, Е'z в S2 соотношениями
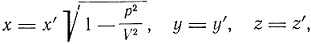
а компоненты сил Ех, Еy, Еz в системе S1 связаны с компонентами Е'x, Е'y, Е'z в S2 соотношениями
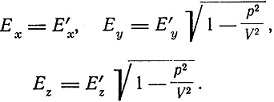
Если предположить, что молекулярные силы в теле, предоставленном самому себе, уравновешиваются для каждой молекулы (при условии, что молекулярное движение не принимается в расчет), и если такое равновесие имеет место в S2, то согласно написанным уравнениям оно будет иметь место и в S1. Поэтому если S2 будет состояние равновесия покоящегося твердого тела, то молекулы в S1 будут занимать положения, характеризуемые координатами х, y, z и связанные с координатами х', y', z' написанными выше соотношениями. Отсюда получается сокращение размеров тела в направлении движения в отношении
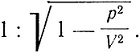
Таким образом, опираясь на принцип относительности первого порядка и введя гипотезу сокращения размеров движущихся тел, Лоренц истолковал оптические явления в движущихся телах, принимая существование неподвижного эфира.
|
ПОИСК:
|