Теория Лармора

Выше мы уже охарактеризовали взгляды Д. Лармора на эфир и материю. Теперь мы рассмотрим более подробно, как Лармор рассматривает проблему электродинамики движущихся сред. В своей книге он дает исторический очерк развития этой проблемы, начиная с открытия Брадлеем аберрации света и кончая опытом Майкельсона. Переходя затем к математическому описанию взаимоотношения движущейся материи и эфира, Лармор использует идею, что частицы материи являются особыми точками (сингулярностями) эфира.

Титульный лист книги Д. Лармора 'Эфир и материя'

Предполагается, что эта сингулярность имеет определенную структуру, образуя ядро напряжения в эфире, способное перемещаться через эфир независимо от движения самого эфира. Часть напряжения эфира, выражаемого вектором смещения (f, g, h)^*, связана с электроном и движется вместе с ним, энергия этой части сконцентрирована вблизи ядра электрона и не может распространяться далеко. Другой вектор, связанный с эфиром, вектор магнитной индукции (а, b, с) не имеет сингулярных полюсов, однако движущийся электрон обладает сингулярностью (a, b, с) вращательного типа с ее ядром в движущемся электроне. Среднее по времени от этой сингулярности для очень быстрого чрезвычайно малого орбитального движения электрона аналитически эквивалентно магнитному диполю. Эфир принимается неподвижным, тогда как молекулы, образующие Землю, и все другие материальные тела перемещаются через него, не вызывая в нем никакого конечного движения. Таким образом, будут строго выполняться закон астрономической аберрации и доплеровское изменение длины волны от движущегося источника излучения. Динамика поля свободного эфира аналитически выражается уравнениями, имеющими место как между электронами, так и вокруг их ядер:

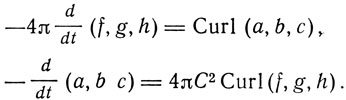
^* (Вектор смещения Максвелла (f, g, h) - в современных обозначениях вектор А вектор индукции (а, b, с) - вектор В.)

Здесь Curl означает операцию вихря, которую при изложении теории Лоренца мы обозначали через rot. Вектор Лармор обозначает с помощью его компонент (а, b, с), частные производные вместе с Максвеллом, обозначений которого он всюду придерживается, он обозначает прямыми дифференциалами ^d/_dx, ^d/_dy и т. д. Величина С - особая константа эфира, представляющая скорость распространения в нем упругих возмущений.

Возникает вопрос о конкретной физической природе векторов (f, g, h) и (а, b, с), характеризующих возмущения в эфире в форме представлений, которые включали бы аналитические соотношения между ними, характеристические свойства электронов и их свободную подвижность через эфир. Однако для аналитической разработки вопроса конкретного физического представления структуры эфира не требуется, достаточную основу дают приведенные выше абстрактные соотношения.

Разрабатывая теорию движущихся материальных сред, Лармор записывает уравнения свободного эфира (уравнения Максвелла) в системе координат х, y, z, покоящейся в эфире, развернутом виде:

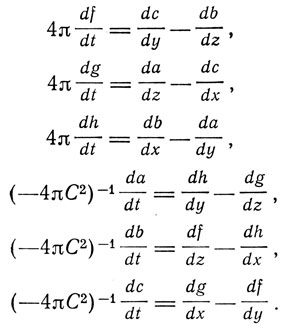
В современных обозначениях

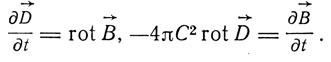
Далее он выписывает эти уравнения в системе (x', y', z'), движущейся равномерно относительно (x, y, z), так что

Обратим внимание, что Лармор считает необходимым записать особо, что t' = t. При таком преобразовании

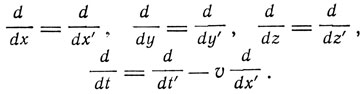
Тогда уравнения поля принимают вид:

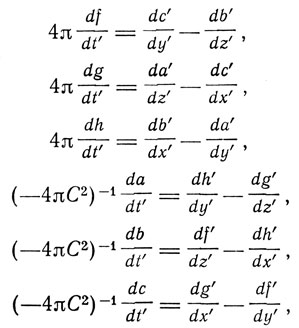
где

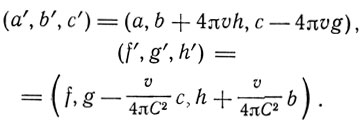
Далее исключаются из этих уравнений нештрихованные величины, так что, например:

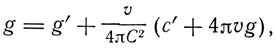
откуда

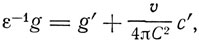
где

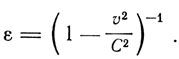
Таким же образом

и вообще

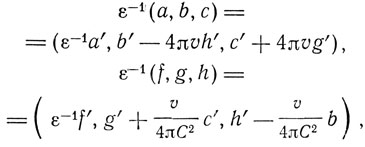
и тогда для движущейся системы

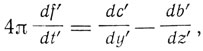
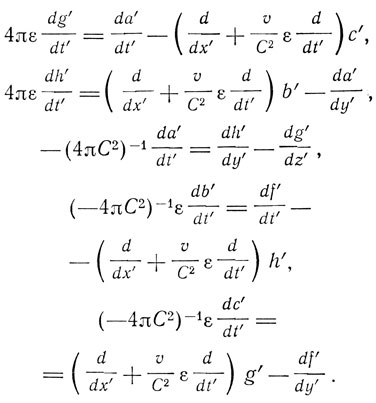
Теперь Лармор делает замечательный шаг. Он вводит новую переменную времени

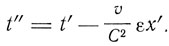
Тогда оказывается, что система уравнений сводится к тому же самому типу, как и в покоящейся системе, за исключением того, что в левой части появляется множитель ε, а именно вид уравнений, отнесенных к осям (x', y', z') и времени t" будет:

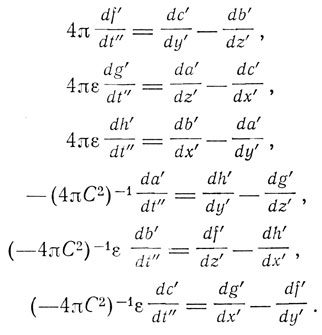
С точностью до первого порядка отношения ^v/_С эти уравнения совпадают с уравнениями в неподвижной среде. Тем самым оказывается справедливым принцип относительности первого порядка. В этом отношении теория Лармора согласуется с теорией Лоренца. Но Лармор идет дальше. Он переходит к новым переменным x₁, y₁, z₁ причем

и вводит новые векторы

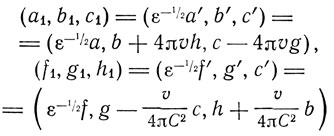
и время t₁, определяемое соотношениями

или

После этих подстановок множитель ε выпадает из уравнений, так что система уравнений для новых переменных с индексами, отнесенными к движущимся осям, совпадает с системой уравнений Максвелла для неподвижных осей.

Нетрудно видеть, что преобразование первоначальных координат (х, y, z, t) в конечные (х₁, y₁, z₁, t₁) совпадает с преобразованиями Лоренца.

Разбирая распространение волн в движущейся среде, Лармор находит, что скорость электромагнитной волны относительно движущейся среды выражается формулой

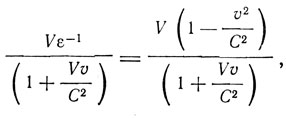
где V = ^C/_μ - скорость света в среде, v - скорость движения среды. Если к этой скорости V волны прибавить скорость среды v, то получится для абсолютной скорости волны в эфире

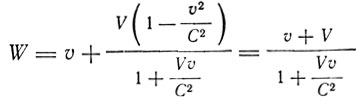
- формула Эйнштейна!

Лармор ограничивается вычислением относительной скорости, которая приближенно равна

Второй член в этом выражении дает коэффициент Френеля. "Оставшийся член,- пишет Лармор,- дает поправку второго порядка согласно нашей гипотезе, которая включает отрицательный результат опыта Майкельсона".

Итак, Лармор находит релятивистскую формулу сложения скоростей и применяет ее для объяснения опыта Физо более чем за пять лет до того, как это было сделано Эйнштейном!

Далее Лармор рассматривает комбинацию положительного и отрицательного электронов, соответствующую позднейшей модели Резерфорда-Бора. Пара электронов противоположного знака образует покоящуюся систему, в которой один электрон описывает вокруг другого круговую орбиту, не излучая. Если эта система движется через эфир со скорстью v, лежащей в плоскости орбиты, то орбита сплющивается в направлении движения в отношении 1 - ¹/₂, ^v2/_C² период обращения при этом изменяется в отношении 1 + ¹/₂, ^v2/_C². То обстоятельство, что период меняется только во втором порядке ^v2/_C² весьма важно для спектроскопических измерений скоростей небесных тел вдоль луча зрения.

В связи с этими результатами Лармор делает общий вывод, что если допустить, что молекулярные силы электрического происхождения, то движение материальной системы через эфир изменяет размеры системы хотя и незначительно, но вполне определенным образом. Таким образом, он приходит к тем же выводам, что и Лоренц, и в связи с этим цитирует "Опыт" Лоренца в той части, которая касается объяснения опыта Майкельсона с помощью сокращения Лоренца-Фитцджеральда. Выше нами были приведены выдержки из этой части работы Лоренца. Следует отметить, что выдержки из Лоренца, приводимые Лармором, вошли позже в сборник работ Лоренца, Пуанкаре, Эйнштейна, Минковского "Принцип относительности". Этот сборник был переведен и на русский язык.

В связи с представлением о взаимодействии атомов через эфир, Лармор указывает, что такое представление не включает в себя непосредственным образом гравитацию. С другой стороны, аналитическая схема, описывающая поведение свободного эфира, данная Мак-Кёллогом и Максвеллом, сводится к линейным уравнениям. Возникает вопрос: не является ли эта линейная схема только первым приближением? Не будут ли относительно незначительные явления, подобные гравитации, описываться с помощью нелинейных членов высшего порядка, входящих в уравнения свободного эфира? Против такой точки зрения говорит субъективное нежелание разрушить идеальную простоту схемы эфира и более весомый факт отсутствия дисперсии свободного эфира для излучения, идущего от небесных тел. Однако незначительность такой дисперсии может быть оценена, если учесть незначительность гравитационного взаимодействия ионов по сравнению с их электрическим взаимодействием. Поскольку эти эффекты возможных нелинейных членов незначительны, предположение, что молекулярные взаимодействия имеют электрическую природу, остается законным. "Таким образом, очень немногое говорит за то, чтобы оставить эту лазейку для объяснения гравитации",- пишет Лармор.

С другой стороны, как указывает Лармор, объяснение любого действия таким путем обязательно имеет отношение к излучению, распространяющемуся со скоростью того же порядка, как скорость света. Но скорость распространения гравитации, если она вообще конечна, значительно превосходит скорость излучения, и потому гравитация не может быть включена в теорию электрических явлений и явлений излучения. Аналогичное имеет место для молекулярных электрических теорий, развитых Вебером, Клаузиусом и др., которые хорошо описывают обычные электрические явления, но несостоятельны для объяснения излучения.

Лармор пытается решить вопрос о гравитации и других возможных неэлектрических взаимодействиях с помощью анализа размерностей. Этот анализ показывает, что если электроны рассматривать как точечные ядра, являющиеся особыми точками эфира, и если возможна какая-либо система электронов (молекула), то возможна и другая система, для которой все линейные размеры (в том числе и размеры молекулы) и промежутки времени (например, период обращения электронов) изменены по отношению к первой в одном и том же отношении, тогда как электрическое и магнитное поля изменяются в другом отношении. Вообще при наличии только электрических действий не может быть определенных однозначно материальных систем, и поэтому если размеры ядер очень малы по сравнению с их взаимным расстоянием, то силы взаимодействия не будут явно зависеть от этих размеров и масс ядер. В случае же наличия неэлектрических действий и конечных размеров ядер размеры молекул будут вполне определенными. Определенность масштаба молекул несовместима с картиной точечных ядер, взаимодействующих друг с другом электрическими силами. Отсюда гравитация не может быть включена явным образом в схему, удовлетворительно описывающую явления электродинамики и оптики. Постоянство размеров материальных атомов обусловливается неэлектрическими силами, зависящими от величины и структуры электрических атомов. Но опыт Майкельсона показывает, что такие силы, если они и существуют, играют совершенно подчиненную роль. Мы не можем сейчас представить таких действий, но, как указывает Лармор, "мы едва ли находимся на пороге структуры атома". Эту структуру, указывает Лармор, мы пока не в состоянии установить так детально, чтобы она описывала весь комплекс химических действий. Лармор заключает, что "много надо постулировать, чтобы отразить главные черты этих универсальных агентов, действующих на все виды материи".

Электромагнитные законы и представление о материи как о совокупности точечных заряженных центров позволили Лармору построить электродинамику движущихся сред. Но он допускал возможность иных неэлектрических действий, в результате которых материя составляется из атомов определенных размеров и которые, возможно, описываются добавочными нелинейными членами в уравнениях эфира.

Рассматривая в дальнейших главах излучение электромагнитной энергии движущимися электронами, Лармор находит известное выражение для потери энергии ускоренных электронов. Формула Лармора имеет вид

где f - ускорение электрона.

Естественно, что Лармора интересует проблема устойчивости молекулы, состоящей из быстро вращающихся электронов. Он устанавливает, что для того, чтобы молекула не теряла энергию на излучение, должно быть выполнено условие: векторная сумма ∑ef должна быть постоянно равна нулю. Это условие не выполняется для системы, состоящей из положительного и отрицательного электронов, вращающихся около друг друга, так как система представляет собой простой диполь - герцевский осциллятор. Однако Лармор полагает, что можно представить модель, удовлетворяющую выдвинутому им условию. Например, этому условию удовлетворяет система положительных электронов, размещенных по кольцу, вращающемуся вокруг внутреннего кольца из отрицательных электронов, находящемуся также во вращении. "Вопрос об устойчивости таких групп, служащих для иллюстрации, дает возможность обширных и интересных математических исследований",- пишет Лармор.

"Весьма поразительный факт,- заключает он параграф своей книги, посвященной этому вопросу, - состоящий в том, что длины волн, излучаемых свободными колебаниями молекул, так велики по сравнению с их диаметрами, настоятельно требует объяснения... По применяемой здесь динамической теории это вызывается тем, что орбитальные скорости электронов имеют примерно такой же порядок малости (превышающий 10^-3) по сравнению со скоростью излучения, какой имеют размеры молекул сравнительно с длинами волн".

Если обозначить V_e орбитальную скорость электрона в атоме, l_a - диаметр атома или молекулы, λ - длину волны излучения, с - скорость распространения излучения, то соотношение, формулируемое Лармором, имеет вид

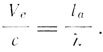
Упоминавшийся уже нами Уайт, подставляя для атомных размеров и длины волны квантовомеханические значения, находит, что

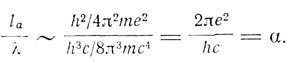
Лармор утверждает, что ^V_e/_c<<1 (α<< 1), иначе система не будет устойчивой. "Энергия орбитальных групп, движущихся с большими скоростями, должна с течением времени чувствительно рассеиваться вследствие излучения, и поэтому такие группы не будут устойчивыми". Это перекликается с воззрениями, высказанными позднее Бором, что концепция стационарных состояний применима только при α<< 1, когда коэффициенты перехода будут достаточно малыми.

На этом мы закончим обзор книги Лармора и вместе с тем характеристику теорий эфира и материи накануне XX столетия. Как видим, в умах физиков такого класса, как Лоренц и Лармор, уже вызревают идеи, разрабатываемые теорией относительности и квантовой теорией материи. Правда, эти идеи появляются в зачаточном и неосознанном виде, но самый факт их появления знаменателен. Он показывает, что физика начала готовиться к прыжку, совершенному ею в XX в.