Неевклидова геометрия

За два года до этой работы Гаусса профессор Казанского университета Николай Иванович Лобачевский представил Ученому совету физико-математического факультета свое знаменитое "Краткое изложение основ геометрии со строгим доказательством теоремы о параллельных".

В этом сочинении Лобачевский изложил основы новой, неевклидовой геометрии. Учению Ньютона-Канта об абсолютном значении евклидова пространства был нанесен сокрушительный удар. Евклидова геометрия перестала быть единственной "истинной" геометрией, постулаты которой Кант считал врожденными истинами. Лобачевский вместо пятого постулата Евклида принял другой. "Начала геометрии" Лобачевского, содержащие новую геометрию, отличную от евклидовой, печатались в "Ученых записках Казанского университета" за 1836, 1837, 1838 гг. В 1840 г. на немецком языке вышел труд Лобачевского "Геометрические исследования по теории параллельных". Во "Вступлении" Лобачевский пишет: "В геометрии я нашел некоторое несовершенство, которое я считаю причиной того, что эта наука, поскольку она не переходит в анализ, до настоящего времени не вышла ни на один шаг за пределы того состояния, в каком она к нам перешла от Евклида".

Таким образом, Лобачевский сразу ставит вопрос о необходимости развития геометрии, которая не может оставаться в том состоянии, как она была оставлена Евклидом. Взамен пятого постулата о параллельных Лобачевский выдвигает свой постулат: "Все прямые линии, выходящие в некоторой плоскости из одной точки, могут быть по отношению к некоторой заданной, прямой той же плоскости разделены на два класса, именно на пересекающие ее и непересекающие. Граничная линия одного и другого класса этих прямых линий называется параллельной заданной линии..."

"При переходе от пересекающих линий AF₁ к непересекающим AG мы должны встретить линию АН, параллельную DC - граничную линию, по одну сторону которой ни одна линия не встречает DC, между тем как по другую сторону каждая линия AF пересекает линию DC. Угол HAD между параллелью АН и перпендикуляром AD называется углом параллели (углом параллельности), мы будем здесь обозначать его через П(Р) при AD = P". В слуги чае если П(Р) = ^π/₂, линии могут быть только пересекающими или параллельными. Для П(Р) < ^π/₂ следует допустить две параллели АН и АК, одну по одну сторону перпендикуляра AD, другую по другую.

Сочинение Лобачевского было прочитано Гауссом, который высоко оценил его, однако только в частной переписке, ставшей достоянием общества в 60-х годах (1860-1863). Гаусс также оценил и значение работы венгерского математика Иоганна Больяи, который в 1837 г. послал Гауссу свое сочинение "Аппендикс" ("Приложение, излагающее абсолютно истинное учение о пространстве, независимо от нерешенной еще a priori истинности или ложности XI евклидовой аксиомы: вместе со случаем ложности рассматривается геометрическая квадратура круга").

Гаусс в письме отцу Иоганна Больяи Вольфгангу пишет, что он "поражен до крайности", "ибо все содержание этого сочинения, путь, выбранный твоим сыном, и результаты, к которым он пришел, совпадают почти целиком с моими собственными размышлениями, начатыми отчасти 30-35 лет тому назад". Гаусс действительно занимался проблемами неевклидовой геометрии, но ничего при жизни не публиковал по этому вопросу, убоявшись, как он сам признавался, "крика беотийцев", т. е. невежественных людей, верящих в геометрию Евклида, как единственно верную геометрию. Между тем творцы неевклидовой геометрии доказали возможность других логических непротиворечивых систем. Вопрос об истинности геометрии, т. е. о соответствии ее законов законам природы, должен решить только опыт. "Поверить в истину геометрии Евклида,- писал Лобачевский,- могут опыты, например астрономические наблюдения". Создание неевклидовой геометрии выдвинуло важную проблему о соотношении геометрии и опыта, о связи геометрических законов с законами природы. Вместе с тем возникла более широкая постановка вопроса о свойствах пространства. Математики стали обсуждать идею многомерного пространства, частным случаем которого является трехмерное. Такая постановка была выдвинута Г. Грассманом в книге "Учение о протяженности" (1844). Здесь же обсуждались более общие классы величин, векторы и тензоры.

Н. И. Лобачевский

Через 10 лет после выхода книги Грассмана, в 1854 г. немецкий математик Бернгард Риман произнес знаменитую речь "О гипотезах, лежащих в основании геометрии". Начиная свою речь, Риман указывает, что "геометрия предполагает заданными как понятие пространства, так и первые основные понятия, которые нужны для выполнения пространственных построений". Он указывает далее, что взаимоотношение между понятиями и аксиомами остается невыясненным. "Причина этому обстоятельству,- говорит Риман,- как я полагаю, заключается в том, что общая концепция многократно протяженных величин, к которым относятся пространственные величины, оставалась вовсе не разработанной". "В связи с этим,- продолжает Риман,- я поставил перед собой задачу, исходя из общего понятия о величине, сконструировать понятие многократно протяженной величины. Мы придем к заключению, что в многократно протяженной величине возможны различные мероопределения и что пространство есть не что иное, как частный случай трижды протяженной величины. Необходимым следствием отсюда явится то, что предложения геометрии не выводятся из общих свойств протяженных величин и что, напротив, те свойства, которые выделяют пространство из других, мыслимых трижды протяженных величин, могут быть почерпнуты не иначе как из опыта".

Б. Риман

Важнейшей гипотезой, принятой Риманом, является гипотеза независимости линий от их положения... "Мероопределение,- говорит Риман,- подразумевает независимость величин от местоположения".

Отсюда он делает допущение, что "длины линий не зависят от их положения, так что каждая линия измеряется посредством каждой".

Вторая гипотеза Римана касается выражения для элемента дуги в пространстве n-измерений. Он полагает, что

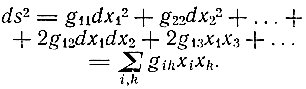
В случае если это выражение сведется к сумме квадратов (теорема Пифагора), пространство называется плоским. Исследуя, при каких условиях пространство будет плоским, Риман вводит величину, которая служит "мерой того, насколько многообразие по данному плоскостному направлению отклоняется от плоского многообразия. Будучи умноженной на -³/₄, она становится равной той величине, которую г. тайный советник Гаусс назвал мерой кривизны поверхности".

Риманова кривизна в отличие от гауссовой является тензорной величиной. При положительной кривизне получается риманово сферическое неограниченное, но конечное пространство. При нулевой кривизне пространство становится плоским, бесконечным евклидовым пространством, и, наконец, при отрицательной кривизне получается псевдосферическое пространство Лобачевского.

Риман ставит глубокий вопрос о причинах, обусловливающих метрику пространства. Он указывает, что р случае дискретности пространства метрика содержится уже в самом понятии дискретного многообразия, но для непрерывного пространства причина метрики кроется во внешних причинах. "Отсюда следует, что или то реальное, что создает идею пространства, образует дискретное многообразие, или же нужно пытаться объяснить возникновение метрических отношений чем-то внешним - силами связи, действующими на это реальное".

Таким образом, Риман поставил во всей общности вопрос о пространстве и его метрических свойствах и показал, что происхождение этих свойств следует искать в физике. "Здесь мы стоим,- заканчивает он свое знаменитое сочинение,- на пороге области, принадлежащей другой науке - физике, и переступать его не дает нам повода сегодняшний день".

Этот порог был перейден Эйнштейном. Однако уже другой физик XIX столетия, Герман Гельмгольц, поставил вопрос о физических фактах, образующих основу геометрии. В 1868 г. появилась работа Гельмольца "О фактах, лежащих в основании геометрии". Она представляла содержание доклада, прочитанного 22 мая 1868 г. в естественно-медицинском обществе Гейдельбёрга. Гельмгольц, работая над основами геометрии, не знал о работах Римана и услышал о них от геттингенского профессора Шеринга, приславшего Гельмгольцу статьи о Римане. "В Вашей заметке о его (Римана) жизни я нашел указание, что он прочитал инавгуральную лекцию о гипотезах геометрии. Я сам последние два года в связи с моими исследованиями по физиологической оптике занимался тем же предметом, но работа еще не закончена и не опубликована, так как я все еще надеюсь, что можно обобщить отдельные результаты". Гельмгольц спрашивает Шеринга, напечатана или будет напечатана работа Римана (она была напечатана в том же 1868 г. в Геттингене) и насколько его результаты перекрывают работу Гельмгольца. Получив от Шеринга ответ, что "существенный момент в исследованиях Римана представляет теорема, что величина, определенная Гауссом в качестве меры кривизны, представляет дифференциальный инвариант для однородного дифференциального выражения второй степени первого порядка с двумя независимыми переменными, Гельмгольц пишет ему 18 мая, что его работа не перекрывается работой Римана, и просит напечатать ее в том же геттингенском журнале, в котором появилась и работа Римана. Гельмгольц показал, что найденное Риманом обобщение теоремы Пифагора будет единственно возможным, если постулировать некоторые предложения о движениях твердых тел. Если существуют факты, касающиеся твердых тел и выведенные из опыта, а именно: 1) твердое тело может свободно двигаться повсюду, где нет другого тела, 2) форма тела не зависит от его вращения, 3) твердое тело может двигаться, если закрепить одну его точку, 4) твердое тело может двигаться и тогда; когда закреплены две точки, и 5) оно неподвижно, когда закреплены три точки, то Гельмгольц приходит к заключению, что единственной мерой длины линейного элемента является длина в форме Римана. При этом он постулирует, что пространство непрерывно и каждая точка его (отдельный элемент) определяется измерением некоторых непрерывных и независимо друг от друга меняющихся величин (координат).

Таким образом, Гельмгольц со всей ясностью показал, что геометрические свойства пространства есть свойства твердых тел. Он пояснял, что в случае бесконечного пространства оно может быть только евклидовым. Бельтрами, давший в том же 1868 г. интерпретацию неевклидовой геометрии и тем самым показавший логическую непротиворечивость геометрии Лобачевского, в письме Гельмгольцу от 24 апреля 1869 г. сообщил, что в случае бесконечного пространства возможна и псевдосферическая геометрия Лобачевского-Больяи. Гельмгольц признал свою ошибку и сообщил об этом в своем докладе Обществу естествоиспытателей в Гейдельберге 30 апреля 1869 г. В 1877 г. выступил со своими исследованиями по теории групп норвежский математик Софус Ли.

Исследуя идеи Гельмгольца, Ли показал, что все перемещения твердого тела образуют группу. Основные свойства пространства: однородность, изотропность, непрерывность, бесконечность - отражаются тем фактом, что перемещения образуют непрерывную бесконечную группу. В связи с исследованиями Ли и Гельмгольца Пуанкаре сказал: "Пространство есть группа". "Если бы не было твердых тел, мы не имели бы геометрии".

Следует далее упомянуть английского математика В. Клиффорда, которому принадлежит знаменитое высказывание о Лобачевском: "Коперник геометрии". Клиффорд настолько проникся идеей о связи геометрии и физики, что одним из первых высказал идею, что чисто физические отношения могут быть выведенными из геометрии. В его сочинении "Здравый смысл точных наук", изданном посмертно Карлом Пирсоном в 1885 г., мы читаем: "Наше пространство может быть действительно тождественно во всех своих частях (имеет одинаковую кривизну), по величине его кривизна может изменяться как целое во времени. В таком случае наша геометрия, основанная на тождественности пространства, сохранит свою силу для всех частей пространства, но перемены в кривизне могут произвести в пространстве ряд последовательных видимых физических изменений".

"Мы можем мыслить наше пространство как имеющее приблизительно однородную кривизну, но легкие изменения кривизны могут существовать при переходе от одной точки к другой, в свою очередь изменяясь во времени. Эти изменения кривизны во времени могут произвести явления, которые мы не так уж неестественно приписываем физическим причинам, не зависящим от геометрии нашего пространства. Мы можем зайти тут настолько далеко, что припишем изменению кривизны даже то, что в "действительности" происходит в явлении, называемом нами "движением материи...". Гипотезам, гласящим, что пространство не гомолоидально (т. е. не евклидово), что его геометрический характер может меняться во времени, быть может, суждено или не суждено сыграть большую роль в физике будущего, но мы не в праве не рассматривать их как возможные объяснения физических явлений, потому что их можно противопоставить повсюду распространенному догматическому верованию во всеобщность известных геометрических теорем, верованию, образовавшемуся благодаря столетиям непрерывного почитания Евклида".

Говоря об этих идеях Клиффорда, А. В. Васильев писал: "Я не мог предполагать, что мне придется дожить до того времени, когда фантастическая теория Клиффорда будет рассматриваться как предвидение математической доктрины, основная идея которой заключается в том, что метрические свойства пространства теснейшим образом связаны с физическими явлениями". Математики, разрабатывая новые основы геометрии, не только укрепляли идеи о тесной связи геометрии и физики, они подготовили также математический аппарат, подходящий для представления такой связи. Учение о кватернионах Гамильтона и Грассмана, разработка основ векторного анализа в теории поля получили свое развитие в работе Риччи и Леви-Чивита "Метод абсолютного дифференциального исчисления и его приложения" (1901), в которой разрабатывалось тензорное исчисление. Математики подготовили почву для развития теории относительности.