Релятивистская динамика

Первым обратил внимание на теорию Эйнштейна Макс Планк, 23 марта 1906 г. он сделал на заседании немецкого физического общества в Берлине доклад "Принцип относительности и уравнения механики". "Физическая идея такой простоты и общности, - говорил он в этом докладе, - какая содержится в принципе относительности, заслуживает того, чтобы ее исследовать..." В связи с этим Планк ставит задачу "определить такую форму основных уравнений механики, которая должна заменить обычное ньютоновское уравнение движения свободной материальной точки:

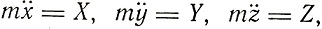
если принцип относительности обладает всеобщим значением". Рассматривая частный случай электромагнитных сил, действующих на заряженное тело, Планк приходит к уравнениям

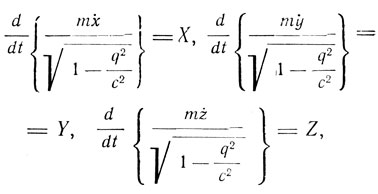
где 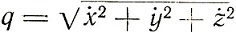- скорость движущейся точки. "Эти уравнения,- пишет Планк,- содержат решение поставленной задачи: они дают требуемое принципом относительности обобщение ньютоновских уравнений движения".

М. Планк

Планк находит далее вид релятивистской функции Лагранжа,

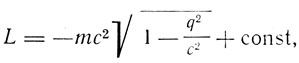
и канонические уравнения Гамильтона в релятивистской форме.

Таким образом, Планк заложил основы релятивистской динамики. В том же 1906 г. Эйнштейн опубликовал работу "Принцип сохранения движения центра тяжести и инерция энергии". В ней он описывает мысленный эксперимент, позволяющий получить зависимость E = mc². Рассматривается замкнутый ящик, на концах которого имеются аппараты I и II, позволяющие посылать и принимать световые импульсы. Если прибор I излучает световой импульс, то согласно электромагнитной теории световой импульс уносит механический импульс и ящик испытывает отдачу. За время, когда свет проходит путь от I к II, ящик движется в противоположную сторону, проходя путь l=ct, где t - время движения, / - длина ящика. При поглощении света приемником II ящик тормозится. Если теперь поменять местами II и I, то при условии равенства масс обоих приборов все остается неизменным, и если теперь заставить II излучать световой импульс, то ящик вновь придет в движение, положение центра тяжести меняется без внутренних изменений, что противоречит закону сохранения движения центра тяжести. Однако закон связи массы и энергии спасает закон сохранения движения центра тяжести. Скорость ящика v при отдаче определяется равенством

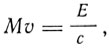
где Е - энергия светового импульса. Ящик перемещается на расстояние

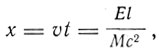
но одновременно импульс уносит массу m на расстояние l. По закону сохранения движения центра тяжести Мх = ml, откуда

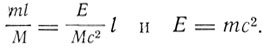
Далее в небольшой заметке Эйнштейн предлагает проект эксперимента по определению массы электрона, который позволил бы сделать выбор между теорией Абрагама и теорией Лоренца-Эйнштейна. Этой заметкой Эйнштейн как бы откликается на дискуссию по поводу опытов Кауфмана, о которой говорилось в предыдущей главе. В 1907 г. Эйнштейн внес новый вклад в развитие теории относительности. В статье "Об инерции энергии, требуемой принципом относительности" Эйнштейн касается вопроса о выводе соотношения E = mc². В его прежнем выводе 1905 г. это соотношение было получено для излучения. Эйнштейн ставит вопрос о необходимости более общего доказательства. "Не могут ли быть частные случаи, несовместимые с законом взаимосвязи массы и энергии?"- спрашивает Эйнштейн. "Ответить на поставленный вопрос в общем виде пока невозможно, так как у нас нет еще полной картины мира, соответствующей принципу относительности",- пишет Эйнштейн. Поэтому он ограничивается рассмотрением двух частных случаев, которые могут быть исследованы методом релятивистской электродинамики. Предварительно Эйнштейн ставит важный вопрос о применимости уравнений Максвелла к пустому пространству. Здесь он ссылается на свою работу по квантовой теории и пишет: "По моему мнению, следует считать, что в свойствах любого периодического процесса есть нечто общее, что превращение энергии может происходить только определенными порциями конечной величины (кванты света), что, следовательно, многообразие возможных в действительности процессов меньше многообразия процессов, возможных согласно нашим теперешним взглядам. В частности, процесс излучения следовало бы представить себе так, чтобы мгновенное электромагнитное состояние в некоторой части пространства полностью определялось конечным числом величин - в противоположность векторной теории излучения".

Итак, Эйнштейн совершенно определенно думает о квантовой теории поля. Однако такой теории еще нет и Эйнштейн временно, "пока в нашем распоряжении еще нет картины, отвечающей указанным требованиям", пользуется классической теорией "во всех вопросах, не касающихся превращений элементарно-малых количеств энергии, а также не затрагивающих соотношений, в которые входит энтропия". Теория Максвелла, по идее Эйнштейна находится в таком же отношении к будущей квантовой теории поля, в каком механика и термодинамика относятся к молекулярно-кинетической теории.

Это замечательное высказывание Эйнштейна приоткрывает завесу над идейными корнями творчества Эйнштейна. Мы уже говорили, что работа Эйнштейна по теории относительности появилась в 17-м томе "Annalen der Physik" вместе с двумя другими работами по квантовой теории излучения и броуновскому движению. Эти на первый взгляд далекие друг от друга исследования Эйнштейн объединяет общей идеей, они представляют собой ступени к какой-то будущей теории, которую можно назвать релятивистской квантовой теорией.

Мы не будем здесь рассматривать конкретные результаты этой работы Эйнштейна, отметим только, что, рассматривая статику твердого тела с точки зрения теории относительности, он указывает здесь, что "если даже релятивистская электродинамика верна, мы еще очень далеки от создания динамики поступательного перемещения твердого тела".

Следующая работа Эйнштейна 1907 г. носит название "О принципе относительности и вытекающих из него следствиях". Эта работа Эйнштейна является важной вехой в развитии теории относительности. Мы процитируем часть вводных замечаний к статье, из которых совершенно ясно виден характер работы и ее новые моменты. "И только представление о световом эфире как носителе электрических и магнитных oсил не находит места в излагаемой здесь теории; напротив, электромагнитные поля оказываются здесь не состояниями некоторой материи, а самостоятельно существующими объектами, имеющими одинаковую природу с весомой материей и обладающими вместе с ней свойством инерции".

Этими словами Эйнштейн вводит в науку новое представление о поле как особой форме материи. Это представление развивает идею, высказанную Фарадеем в 1852 г. Рассматривая вопрос о физических линиях силы, которые, по Фарадею, являются образами поля, Фарадей указывает, что в случае света "лучи (которые представляют собой световые линии) проходят через промежуточное пространство, но здесь мы можем оказать на эти линии действие при помощи различных сред, расположенных на их пути". "Мы можем,- продолжает Фарадей,- отразить их от их источника и затем искать их - найти, прежде чем они достигнут своей конечной цели. Они связаны со временем и требуют 8 минут, чтобы пройти от Солнца до Земли; таким образом, они могут существовать независимо (курсив мой.- П. К.) и от своего источника, и от места, в которое они в конце концов приходят.

Таким образом, они имеют ясно различимое физическое существование (курсив мой.- П. К.).

Таким образом, идея поля, имеющего самостоятельное физическое существование, была высказана более чем за полвека до Эйнштейна. Однако в науке после Максвелла прочно укоренилось мнение, что Фарадей рассматривал поле как состояние натяжений и давлений в эфире, хотя именно Фарадей полагал, что идея самостоятельного существования магнитных силовых линий может избавить нас от эфира. Эйнштейн высоко ценил заслуги Фа-радея и особо отмечал его приведенные здесь взгляды на поле.

"Фарадею,- писал Эйнштейн,- принадлежит также смелая мысль о том, что при известных условиях поля могут отрываться от порождающих их тел и двигаться далее по пространству в виде свободных полей: это и была его интерпретация света". Интуитивную идею Фарадея о поле как самостоятельной физической реальности воспринял и развил Эйнштейн.

Содержание своей работы Эйнштейн характеризует следующим образом: "Ниже делается... попытка свести в единое целое работы, которые возникли до настоящего времени путем объединения теории Г. А. Лоренца и принципа относительности.

В первых двух частях работы рассматриваются кинематические основы теории, а также применение их к основным уравнениям теории Максвелла-Лоренца. При этом я следовал работам Лоренца и своей".

В первой части, где излагаются исключительно кинематические основы теории, рассмотрены также некоторые задачи оптики (принцип Доплера, аберрация, увлечение света движущимися средами); на возможность такого способа рассмотрения было обращено внимание М. Лауэ в беседе с ним, а также работой последнего и работой (правда, требующей уточнения) Н. Лауба. В третьей части развивается динамика материальной точки (электрона). Для вывода уравнений движения применен тот же метод, что и в названной выше работе автора. Сила определена, как в работе Планка. Из этой работы взяты и преобразования уравнений движения материальной точки, которые так отчетливо выявляют аналогию уравнений движения с уравнениями классической механики.

Четвертая часть посвящена общим следствиям, к которым приводит теория относительности и которые касаются энергии и количества движения физических систем. Эти следствия были развиты в оригинальных работах автора, а также М. Планка. Однако здесь они получены новым путем, который, как мне кажется, позволяет особенно ясно проследить связь этих выводов с основами теории. Здесь рассматривается также зависимость энтропии и температуры от состояния движения; в вопросе об энтропии я полностью придерживаюсь только что цитированной работы Планка, температуры движущихся тел я определяю так же, как г-н Мозенгайль в своей работе о движущейся полости, содержащей излучение.

Важнейшим результатом четвертой части является следствие об инертной массе энергии. Этот результат наводит на мысль о том, не обладает ли энергия также тяжелой (гравитирующей) массой. Далее напрашивается вопрос, ограничен ли принцип относительности системами, движущимися без ускорения. Чтобы не оставить эти вопросы без разъяснения, я добавил к этой работе пятую часть, которая содержит новое релятивистское рассмотрение ускорения и гравитации".

Отсюда видно, что Эйнштейн уже начал переход от специальной теории относительности к общей. Его работа 1907 г. является первым шагом на этом пути. Общая теория относительности будет излагаться в этой книге в главе "Тяготение", и здесь мы будем ограничиваться лишь упоминанием о работах по общей теории относительности этого-периода.

В приведенной выше цитате Эйнштейн упоминает о работах Лауэ" Лауба и Планка, относящихся к тому же 1908 г. Лауб указал (хотя и неудачно) на возможность объяснения френелевского коэффициента увлечения. Лауэ дал это объяснение. Напомним, что впервые оно было дано из той же формулы сложения скоростей Лармором. Однако ни один из упомянутых здесь авторов, включая Эйнштейна, не упоминает о попытке Лармора. По-видимому, она оставалась им неизвестной.

Работа Планка, процитирован-г ная Эйнштейном, дает анализ термодинамических понятий с точки зрения теории относительности. Планк устанавливает, что энтропия является инвариантной величиной, а абсолютная температура тела меняется со скоростью аналогично изменению объема (или длины): Т = T₀√(1-β²). Упомянутый Эйнштейном Мозенгайль занимался той же задачей, что и Газенорль, а именно излучением движущейся полости. Как мы упоминали в предыдущей главе, Газенорль, рассматривая эту проблему, установил соотношение между энергией и массой. Результат Газенорля был неточен (в формуле связи был коэффициент ⁴/₃). Мозенгайль рассмотрел зависимость светового давления, энергии, импульса, энтропии от температуры и скорости движения. Для неподвижной полости

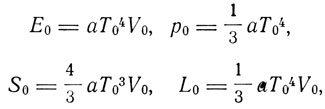
где E₀ - энергия излучения в объеме V₀, p₀ - давление, S₀ - энтропия,

- постоянная Стефана, L₀ - действие. Для движущейся полости будет:

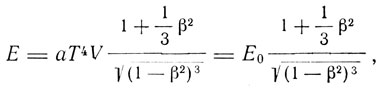
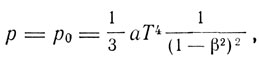
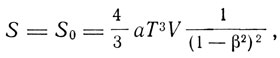
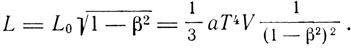
Для импульса получаем

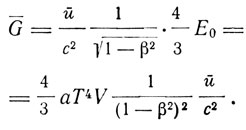
Эти выводы, содержащиеся в диссертации рано умершего физика К. Мозенгайля, были использованы Планком для обоснования релятивистской динамики.

Таким образом, менее чем через два года после возникновения теории относительности Эйнштейна, выводы ее широко проникли в механику, термодинамику, оптику и электродинамику.