Теория Минковского

В 1908 г. теория относительности получила новое чрезвычайно важное развитие. 21 сентября этого же года на съезде немецких естествоиспытателей и врачей в Кёльне вы ступил со своим знаменитым докладом "Пространство и время" учитель Эйнштейна по цюрихскому политехникуму Герман Минковский. "Воззрения на пространство и время, которые я желал бы развить перед вами, возникли на почве физических опытов. В этом их сила. Тенденция их радикальная. Отныне время по себе и пространство по себе должны сделаться всецело тенями и только особого рода их сочетание сохранит самостоятельность". Этими, ставшими знаменитыми словами Минковский начинает свой доклад. Значение этого смелого высказывания Минковского раскрывается в его докладе. "Предмет нашего восприятия,- говорит он,- всегда составляет только места и времена, вместе взятые. Никто не замечает никогда места иначе, как в определенное время, или время иначе, как в определенном месте... Точку пространства в точке времени, т. е. систему значений x, y, z, t я назову мировой точкой. Многообразие всех мыслимых систем значений x, y, z, t пусть называется миром". Этот четырехмерный мир и позволяет Минковскому геометрически интерпретировать законы теории относительности. Он связывает с мировой точкой некоторую субстанцию. Движение этой субстанциональной точки в пространстве и времени изобразится в мире Минковского кривой линией - мировой линией. "Весь мир,- пишет Минковский,- является разложенным на подобного рода мировые линии, и я позволю себе сейчас высказать мнение, что физические законы найдут свое совершеннейшее выражение как взаимоотношения между этими мировыми линиями".

Г. Минковский

Преобразования Лоренца в системе Минковского представляют собой вращения координатных осей, оставляющие инвариантным четырехмерный вектор, квадрат длины которого

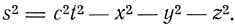
Величина s называется пространственно-временным интервалом. Четырехмерные вектора s Минковский разделяет на временно-подобные, для которых s²>0, и пространственно-подобные, для которых s²<0. Из временно-подобных векторов особое значение имеет величина

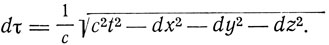
"Интеграл ∫dτ = τ этого значения на мировой линии от какой-нибудь фиксированной начальной точки Р₀ до переменной конечной точки Р мы называем собственным временем субстанциональной точки Р".

Определяя производные от координат мировой точки по собственному времени, мы находим компоненты четырехмерного вектора скорости, квадрат величины которого, по Минковскому, равен с² (Минковский называет этот временно-подобный вектор вектором движения), и нормальный к этому вектору пространственно-подобный вектор ускорения, получаемый вторичным дифференцированием координат по собственному времени τ. Таким образом, кинематика теории относительности получает у Минковского наглядную геометрическую интерпретацию. Минковский далее развивает и динамику, введя постоянную массу точки m и компоненты четырехмерного вектора силы.

Минковский завершил дело создания специальной теории относительности, которая получила ясную и законченную математическую формулировку. Теперь теория относительности становится достоянием учебников и монографий. В 1909 г. М. Планк прочитал в США восемь лекций по теоретической физике. Последние две лекции были посвящены изложению основ теории относительности. В этих лекциях Планк дает краткий исторический очерк развития теории относительности, начиная с Галилея и кончая Лоренцем и Фитцджеральдом. Указав, что теория относительности сделала ненужным эфир, Планк пишет: "Вместо так называемого свободного эфира вступает абсолютная пустота, в которой электромагнитная энергия распространяется так же самостоятельно, как и весомые атомы. Я считаю только последовательным, что абсолютной пустоте не приписывается каких-либо физических свойств".

Но теория относительности привела также к новому понятию времени, и Планк подчеркивает: "Это новое понятие о времени, конечно, требует от физика большой способности к абстракции и большой силы воображения. Оно превосходит по своей смелости все, что было сделано до сих пор в области умозрительного естествознания и в философской теории познания; в сравнении с этим неевклидова геометрия - не больше, как детская игрушка. Между тем в противоположность неевклидовой геометрии, имеющей пока серьезное значение только для чистой математики, принцип относительности с полным правом претендует на реальное физическое значение. По широте и глубине вызываемого им переворота в области физического мировоззрения с ним можно сравнить разве введение коперниковской системы мира".

В 1910 г. Эйнштейн в обширной статье "Принцип относительности и его следствия в современной физике" систематизировал свои результаты и результаты Минковского. Четко и последовательно он показывает необходимость изменения пространственно-временных представлений и принципа относительности. Сам принцип он формулирует дважды. Первая формулировка гласит: "Законы, управляющие явлениями природы, не зависят от состояния движения системы координат, по отношению к которым эти явления наблюдаются, если эта система движется без ускорения". При этом Эйнштейн предполагает, что ускорение имеет объективное, т. е. абсолютное, значение, поскольку наблюдатель всегда может констатировать ускорение своей системы координат. Вторая формулировка основана на идеях Минковского; она гласит: "Принцип относительности требует, чтобы законы физики не изменялись от вращения четырехмерной системы координат, к которой они относятся. Четыре координаты x₁, x₂, x₃, x₄ должны входить в выражения законов природы симметрично. Для описания различных физических состояний можно пользоваться четырехмерными векторами, которые входят в вычисления точно так же, как и обычные векторы трехмерного пространства".

В 1910 г. вышел "Курс электричества и магнетизма" Густава Ми. В нем имеются параграфы, посвященные теории относительности. В предисловии автор пишет: "Теория относительности в той форме, которую ей придал Минковский (Minkowski), приводит к заключению, что физический мир, собственно, является четырехмерным и что существует одна только форма восприятия четырех измерений, именно пространство - время". В следующем, 1911 г. вышло первое издание монографии М. Лауэ (Die Relativitats Theorie", ставшей одним из популярных курсов теории относительности. В предисловии автор писал: "За 5¹/₂ лет, прошедших со времени обоснования Эйнштейном теории относительности, эта теория во все более возрастающей степени привлекала внимание. Конечно, это внимание не всегда означало согласие. Многие исследователи, и среди них носители очень известных имен, считали ее эмпирическое обоснование недостаточным. Сомнения подобного рода, естественно, можно устранить лишь дальнейшими опытами: все же предлагаемая книжка придает большее значение доказательству того, что не существует никаких эмпирических оснований против этой теории. Но значительно больше число тех, кто недружелюбно относится к ее идейному содержанию, именно те, кому кажется неприемлемой относительность времени с ее подчас действительно очень парадоксальными следствиями. И здесь, может быть, окажется полезным связное изложение теории, как оно будет дано в этой книжке".