Первые следствия принципа эквивалентности

Уже в работе 1907 г., как ранее было сказано, Эйнштейн попытался вывести из принципа эквивалентности следствия, относящиеся к масштабам и часам, а также к распространению света в поле тяготения. Кроме того, он показал, что для потенциальной энергии "тяжелой" массы в поле тяжести выполняется соотношение

К этим результатам он вернулся через четыре года по той причине, что его, как он сам пишет в начале новой статьи, "не удовлетворяет прежнее изложение вопроса". В этой новой статье "О влиянии тяжести на распространение света" он прежде всего разбирает вопрос о тяжести энергии. Этот вопрос он разбирает с помощью мысленного эксперимента. Имеются две системы "S₁ и S₂, размеры которых малы по сравнению с их взаимным расстоянием h в направлении поля тяготения, так что гравитационный потенциал в системе S₂ на γh больше потенциала в системе S₁. Из S₂ посылается в S₁ в виде излучения энергия Е₂. Введем систему отсчета К₀, не обладающую ускорением, и ускоренную систему отсчета К'. В момент излучения системой S₂ энергии Е₂ пусть эта система отсчета К' обладает относительно Ко нулевой скоростью. Спустя промежуток времени, равный в первом приближении t = ^h/_c, энергия Е₂ достигает S₁. В этот момент система S₁ обладает относительно К₀ скоростью

и по специальной теории относительности энергия, воспринятая S₁ будет E₁, причем

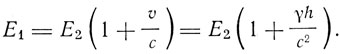
По принципу эквивалентности то же самое справедливо для покоящейся системы отсчета К, находящейся в гравитационном поле с потенциалом Ф = γh, поэтому

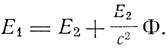
Эйнштейн поясняет с помощью воображаемого кругового процесса, что это соотношение эквивалентно утверждению о приращении тяжелой массы на величину ^E/_c². Таким образом, тяжелая масса, как и инертная, удовлетворяет закону пропорциональности массы и энергии

Далее из принципа эквивалентности следует, что "луч света, испускаемый в области с определенным потенциалом тяготения из S₂ и имеющий при его испускании частоту v₂, измеренную часами, находящимися в S₂, обладает при его прибытии в S₁ другой частотой v₁, если последняя измеряется с помощью точно таких же часов, находящихся в S₁". Если потенциал тяготения в S₂, взятый по отношению к S₁ равен Ф, то

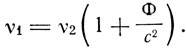
Если, например, частота источника света, находящегося на Солнце и измеренная с помощью находящихся там же часов, равна v₀, то на Земле частота света, испускаемого этим источником и измеренная часами той же конструкции, будет иной, равной v. При этом

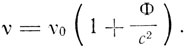
"Таким образом,- заключает Эйнштейн,- согласно нашим представлениям спектральные линии солнечного света должны несколько сместиться по сравнению с соответствующими спектральными линиями земных источников в сторону красного конца спектра, а именно на относительную величину

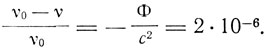
Это смещение можно было бы измерить, если бы были точно известны условия, при которых испускается солнечный свет".

Этот важный вывод связан с неодинаковостью хода часов в разных местах гравитационного поля. Вместе с тем скорость света не остается инвариантной величиной, какой она была в специальной теории относительности. Если скорость света в месте с нулевым гравитационным потенциалом равна с₀, то в некотором месте с потенциалом Ф она будет равна с, причем

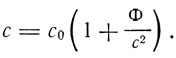
Из этого факта с помощью принципа Гюйгенса получается искривление световых лучей в поле тяготения. Это отклонение на любом пути s, взятое в сторону возрастания n', будет

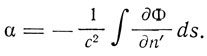
По этой формуле луч света, проходящий мимо какого-либо небесного тела, испытывает отклонение в сторону убывания гравитационного потенциала, т. е. в сторону небесного тела, равное

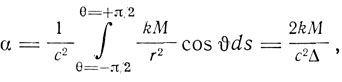
где k - гравитационная постоянная, М - масса небесного тела, Δ - расстояние от луча до центра небесного тела. "По этой причине,- подчеркивает Эйнштейн,- луч света, проходящий мимо Солнца, испытал бы отклонение, равное 4*10^-6 = 0,83 дуговой секунды". На самом деле, отклонение Должно быть вдвое больше, поскольку Эйнштейн во всех этих расчетах не принимал во внимание искривление пространства. Впоследствии В. Паули писал по поводу этих первых работ Эйнштейна: "Уже эта теория однородного гравитационного поля выходила из рамок специальной теории относительности. Вследствие зависимости скорости света и скорости хода часов от гравитационного потенциала... преобразования Лоренца теряют свой смысл". Это обстоятельство вынуждало физиков искать путей согласования теории относительности с теорией тяготения. Нордстром в 1912 г. попытался это сделать, предположив, что принципы специальной теории относительности (постоянство скорости света, инвариантность уравнений относительно преобразований Лоренца) сохраняются и в поле тяготения. В его теории соблюдаются законы сохранения энергии и импульса и равенство инертной и гравитационной массы. Но она не дает искривления светового луча в поле тяжести, дает неправильный знак движения перигелия Меркурия. В том же году теорию гравитации построил М. Абрагам, а Эйнштейн выступил со статьей "Скорость света и статическое гравитационное поле", в которой он заявил, что то обстоятельство, что принцип эквивалентности привел к следствиям, несовместимым с преобразованиями Лоренца, не должно "отпугивать от дальнейшего следования по избранному пути". Вскоре он опубликовал новую работу "К теории статического гравитационного поля". Далее ему пришлось вступить в полемику с Абрагамом, который заявил, что Эйнштейн "нанес завершающий удар теории относительности, отказавшись от постулата постоянства скорости света и от связанной с ним инвариантности системы уравнений относительно преобразований Лоренца". Эйнштейн в ответ на это указывает, что "сомневаться во всеобщей справедливости принципа относительности у нас нет ни малейшего основания". Однако он полагает, что "принцип постоянства скорости света можно сохранить лишь до тех пор, пока мы ограничиваемся пространственно-временными областями с постоянным гравитационным потенциалом".

Далее Эйнштейн высказывает убеждение, что "Задачей ближайшего будущего должно быть создание релятивистской схемы, в которой найдет свое выражение эквивалентность инертной и тяжелой массы". Указав на свои попытки создать теорию статического гравитационного поля, Эйнштейн, однако, констатирует: "Необходимо признать, что эту интерпретацию мы смогли провести только для бесконечно малых областей пространства и что не можем указать никакого удовлетворительного объяснения этого обстоятельства". Несмотря на это, Эйнштейн считает, что нет "никаких оснований для того, чтобы отказаться от принципа эквивалентности также и для бесконечно малых областей". Этот принцип, как думает Эйнштейн "открывает нам интересную перспективу - уравнения теории относительности, охватывающей гравитацию, должны быть инвариантны также относительно преобразований ускорения (и вращения)".

"Однако,- заканчивает Эйнштейн,- путь к этой цели представляется нам весьма трудным".