Создание общей теории относительности

Но уже в следующем, 1913 г. появилась совместная работа Эйнштейна и его друга М. Гроссмана, которому принадлежала математическая часть "Проект обобщенной теории относительности", в которой Эйнштейн сделал первую удачную попытку распространить принцип относительности и на неравномерные движения систем отсчета. Чтобы получить уравнения движения материальной точки, инвариантные относительно произвольного преобразования

Эйнштейн записывает эти уравнения в виде вариационного принципа

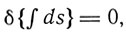
где

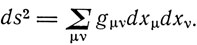
"Таким образом, мы приходим к убеждению, что в общем случае гравитационное поле характеризуется десятью пространственно-временными формами

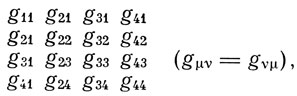
которые в случае обычной теории относительности соответственно равны

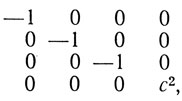
где с - постоянная".

Написав функцию Гамильтона H в виде

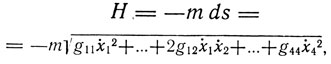
Эйнштейн получает выражения для импульса I и энергии Е материальной точки, а также для силы, действующей на точку со стороны гравитационного поля. Фундаментальные величины образуют инвариантный тензор второго ранга, импульс и энергия совместно образуют четырехмерный вектор.

Эйнштейн пытается построить дифференциальные уравнения для поля тяготения, аналогичные уравнениям Пуассона в теории потенциала. В это уравнение взамен потенциала тяготения Ф должна войти компонента тензора поля тяготения g_uv. Ему не удалось получить ко-вариантного уравнения. Построенные им уравнения оказались ковариантными только относительно линейных преобразований. Эйнштейн утверждал, что "при современном состоянии теории мы не можем требовать инвариантности уравнений относительно произвольных преобразований".

В докладе на 85-м съезде немецких естествоиспытателей и врачей в Вене Эйнштейн следующим образом формулирует предпосылки,

на которых должна основываться теория гравитации. Эти предпосылки следующие:

1. "Выполнение законов сохранения импульса и энергии.
2. Равенство инертной и тяжелой масс замкнутых систем.
3. Справедливость теории относительности (в более узком смысле), т. е. система уравнений должна быть ковариантной относительно линейных ортогональных подстановок (обобщенные преобразования Лоренца).
4. Наблюдаемые законы природы не должны зависеть от абсолютных значений гравитационного потенциала (или гравитационных потенциалов). Физически это означает следующее: совокупность связей между наблюдаемыми величинами, которую можно найти в некоторой лаборатории, не должна меняться, если всю лабораторию переместить в область с другим гравитационным потенциалом (постоянным в пространстве и времени)".

Эйнштейн еще не уверен, что все эти постулаты необходимы для построения релятивистской теории тяготения. В частности, Абрагам строил теорию тяготения без третьего постулата. Четвертый постулат, как полагает Эйнштейн, "вероятно, нельзя обосновать опытом. Он,- продолжает Эйнштейн,- оправдывается не чем иным, как верой в простоту законов природы, и мы не можем полагаться на то, что он выполняется с таким же правом, как в случае остальных трех упомянутых аксиом". "Мы прекрасно сознаем,- заканчивает Эйнштейн,- что постулаты 2-4 похожи скорее на научный символ веры, нежели на надежный фундамент".

Итак, Эйнштейн еще сомневается в надежности и однозначности постулатов, на которых должна строиться теория тяготения. Тем более он сомневается в том, что полученные им результаты являются единственно возможными. Все же он считает их наиболее естественными.

Колебания Эйнштейна нашли свое отражение в его отношении к теории Нордстрема, в которой гравитационное поле описывается скалярной величиной. В основной статье 1913 г. он считает концепцию скалярного поля неприемлемой. Однако в докладе на Венском съезде немецких естествоиспытателей и врачей, происходившем осенью того же года, он снимает свои возражения и считает, что теория Нордстрема, опирающаяся на постулат постоянства скорости света, "удовлетворяет всем требованиям, которые при современном состоянии эксперимента можно предъявить теории гравитации".

Другим пунктом сомнения Эйнштейна, наиболее важным в принципиальном отношении, является вопрос о ковариантности уравнений гравитационного поля относительно произвольных преобразований пространства и времени. Полученное им в работе 1913 г. тензорное уравнение

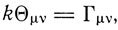
где k - гравитационная постоянная,

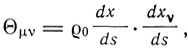
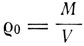
- плотность масс - ковариантный тензор второго ранга, Г_μv - контравариантный тензор второго ранга, образованный из производных фундаментального тензора g_μv, не является ковариантным относительно произвольных преобразований. Эйнштейн далее пишет, что "у нас нет никаких оснований для общей козариантности уравнений гравитации". Далее в докладе "Физические основы теории тяготения", сделанном в 1913 г. на годичном собрании Швейцарского общества естествоиспытателей, он категорически утверждает: "Из общих соображений можно показать, что уравнения, полностью определяющие гравитационное поле, не могут быть ковариантными относительно произвольных преобразований".

В венском докладе он пишет, что "проблема гравитации была бы решена удовлетворительно, если бы удалось найти ковариантные относительно произвольных преобразований уравнения, которым удовлетворяет гравитационное поле g_μv.

"Однако,- добавляет Эйнштейн,- o решить проблему таким способом не удалось".

Эйнштейн полагает, что можно отказаться от требования ковариантности в общем виде и потребовать только, чтобы уравнения удовлетворяли законам сохранения и были ковариантными относительно линейных преобразований.

Таким образом, к концу 1913 г. сомнения Эйнштейна относительно требования ковариантности разрешаются тем, что Эйнштейн считает возможным вообще отказаться от этого требования. В течение 1914 г. Эйнштейну приходится дискутировать по основным вопросам теории тяготения, в частности отвечать на критику Г. Ми. В ответе Ми Эйнштейн признает, что его теория еще несовершенна. "Это несовершенство,- пишет Эйнштейн,- связано с тем, что в некоторых отношениях я сам еще не пришел к полной ясности".

Вскоре после полемики с Ми Эйнштейн выступил с большой статьей "Формальные основы общей теории относительности", в которой сделал попытку изложить математические основы новой теории тяготения. Эйнштейн в вводных соображениях очень ясно обосновывает необходимость перехода от специальной теории относительности к общей. Специальная теория относительности имеет дело с классом "привилегированных" систем отсчета, инерциальных систем. Но кинематика не знает таких привилегированных систем. "Поэтому представляется необходимым обобщить существующую теорию относительности таким образом, чтобы устранить из нее кажущееся несправедливым предпочтение равномерных и прямолинейных движений перед относительными движениями других типов. Необходимость подобного расширения теории должен почувствовать каждый, кто обстоятельно знаком с предметом".

Но динамика не позволяет сделать такого обобщения. Переход от инерциальной системы к неинерциальной требует введения "сил инерции". "Однако,- пишет Эйнштейн,- этот аргумент, как, в частности, показал Э. Мах, не обоснован. Существование центробежных сил в действительности не обязательно основывается на движении самой системы К. С таким же успехом мы можем их приписать среднему вращательному движению весомых удаленных масс в окрестности системы по отношению к К', причем систему К' мы считаем покоящейся". Это дает возможность "рассматривать вращающуюся систему К' как покоящуюся и интерпретировать поле центробежных сил как некоторое гравитационное поле". "Из сказанного следует,- заключает Эйнштейн,- что в теории относительности, обобщенной в указанном смысле, гравитация должна играть фундаментальную роль. Если посредством некоторого преобразования перейти от системы отсчета К к системе отсчета К', то относительно системы К.', вообще говоря, существует некоторое гравитационное поле; при этом нет необходимости, чтобы поле существовало бы и в системе К".

Таким образом, задача обобщения специальной теории относительности оказывается неразрывно связанной с проблемой гравитации. Формальный аппарат общей теории относительности, как это было показано в статье Эйнштейна-Гроссмана 1913 г., содержится в тензорном исчислении. Мы можем отметить, что в истории теоретической физики каждый новый шаг сопровождается новыми требованиями к математическому аппарату. Ньютон, закладывая основы классической механики, был вынужден создать новый математический аппарат - дифференциальное и интегральное исчисление. И хотя он излагал в своем основополагающем труде новые идеи на языке старой геометрии, было ясно, что старая геометрия не могла соответствовать новым задачам. Максвелл, создавая новые основы теории электрических и магнитных явлений, был вынужден использовать новый математический язык, язык векторного исчисления Гамильтона-Грассмана. Теперь Эйнштейн, создавая общую теорию относительности, опирался на математический аппарат тензорного анализа, основы которого были заложены еще в работе Кристоффеля 1869 г. "О преобразовании однородных дифференциальных выражений второго порядка" и были развиты Риччи-Леви-Чивита в работе 1901 г. "Методы абсолютного дифференциального исчисления".

В разбираемой нами работе Эйнштейн излагает основные понятия четырехмерного векторного и тензорного исчисления, дает понятия ковариантного и контравариантного вектора, ковариантного, контравариантного и смешанного тензоров второго и высшего ранга и определяет основные операции тензорного исчисления.

Но одного математического аппарата еще не достаточно для построения физической теории. Получить правильные уравнения тяготения Эйнштейну в этой работе еще не удалось. Однако Эйнштейн делает в этой работе важный шаг вперед. Он ясно видит, что новая теория тяготения должна быть теорией близкодействия, а не дальнодействия, какой была теория тяготения Ньютона. Именно в этом важном пункте Эйнштейн порывает с Махом, принцип которого, по существу, был дальнодействующим принципом. В своей автобиографии Эйнштейн писал: "По мнению Маха, в действительно рациональной теории инертность должна, подобно другим ньютоновским силам, происходить от взаимодействия масс. Это мнение я долгое время считал в принципе правильным. Оно неявным образом предполагает, однако, что теория, на которой все основано, должна принадлежать тому же общему типу, как ньютонова механика: основными понятиями в ней должны служить массы и взаимодействия между ними. Между тем нетрудно видеть, что такое понятие не вяжется с духом теории поля".

Но отказ от ньютоновской концепции влечет за собой и другой важный вывод; его со всей ясностью подчеркивает Эйнштейн в разбираемой нами работе 1914 г.:

"Благодаря Максвеллу с тех пор в физике произошел решительный переворот, во время которого постепенно победило представление о том, что в элементарных законах расстояния между конечноудаленны-ми точками не могут появляться, т. е. "теория дальнодействия" была заменена "теорией близкодействия". При этом, однако, забылось, что евклидова геометрия в том виде, как она применялась в физике, также состоит из физических утверждений, которые с физической точки зрения устанавливались из интегральных законов ньютоновской механики точки. Это означает, на мой взгляд, некоторую непоследовательность, от которой нам нужно освободиться".

Первая страница оригинала статьи Эйнштейна 'Основы общей теории относительности'

Так возникает фундаментальный для общей теории относительности вопрос о характере геометрии, соответствующей новой теории. Эйнштейн чувствует, что возможность использований в этой теории евклидовой геометрии, сведенной к дифференциальным соотношениям в духе теории близкодействия, "отнюдь не является наиболее простой и очевидной".

1915-й год продвинул дело создания общей теории относительности еще дальше. Эйнштейн подверг критическому пересмотру все сделанное им до сих пор и пришел к выводу, что шел по неверному пути. Очень резко и самокритично он пишет в статье "К общей теории относительности", что, "следуя по предложенному пути, совершенно невозможно ничего доказать; то, что казалось все же сделанным, было основано на заблуждении". "По этим причинам,- пишет далее он,- я полностью потерял доверие к полученным мною уравнениям поля и стал искать путь, который ограничивал бы возможности естественным образом. Так я вернулся к требованию более общей ковариантности уравнений поля, от которой я отказался с тяжелым сердцем, когда работал вместе с моим другом Гроссманом".

В новой теории Эйнштейн требует ковариантности всех систем уравнений относительно преобразований, определитель Якоби для которых равен:

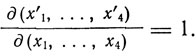
Таким образом, Эйнштейн переходит от линейных к более общему классу преобразований, но все же ограниченному написанным здесь условием ("условием унимодульности").

Он очень близко подошел к правильным уравнениям теории гравитации и в следующей за этой работой заметке получил из своих уравнений объяснение движения перигелия Меркурия, решив, таким образом, задачу, представлявшую для ньютоновской теории тяготения непреодолимое препятствие. Кроме того, он установил, что следствием новой теории "является более сильное (в два раза большее) искривление светового луча гравитационным полем по сравнению с нашими прежними исследованиями".

В 1916 г. появилась фундаментальная работа Эйнштейна "Основы общей теории относительности", которой завершался напряженный период исканий и закладывались основы общей теории относительности. "Излагаемая здесь теория,- писал Эйнштейн в первых строках своей классической работы,- является наиболее радикальным обобщением общеизвестной в настоящее время "теории относительности"; последнюю в отличие от первой я буду называть "специальной теорией относительности", предполагая, что с нею читатель знаком".

Таким образом, употребительные в настоящее время термины "специальная" и "общая" теория относительности ведут свое происхождение от основополагающей работы Эйнштейна 1916 г.

Далее Эйнштейн четко формулирует основные принципы, лежащие в основе теории. Постулат относительности расширяется и теперь формулируется следующим образом:

"Законы физики должны быть составлены так, чтобы они были справедливы для произвольно движущихся систем".

Математически это требование выражается так:

"Общие законы природы должны быть выражены через уравнения, справедливые во всех координатных системах, т. е. эти уравнения должны быть ковариантными относительно любых подстановок (общековариантными)".

Итак, если в работе 1913 г. Эйнштейн требовал от уравнений ковариантности по отношению к линейным преобразованиям, в работе 1914 г. он требовал ковариантности относительно произвольных преобразований, ограниченных, однако, условием равенства детерминанта преобразований единице, то в работе 1916 г. он четко сформулировал постулат общековариантности. Вместе с принципом эквивалентности этот постулат дает основу для построения теории тяготения. В этой теории инвариантом, не зависящим от выбора пространственных и временных координат, является величина

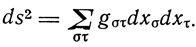
При этом "величины g_στ с физической точки зрения должны рассматриваться как величины, описывающие гравитационное поле относительно выбранной системы координат". С другой стороны, "По функциям gox, представляющим гравитационное поле, определяют в то же время метрические свойства четырехмерного пространства".

Математический аппарат тензорного исчисления изобилует выражениями, в которых производится суммирование по текущим значкам, вроде выражения для ds². Как видно из этого выражения, значки, по которым производится суммирование (здесь σ и τ), встречаются под знаком суммы дважды. Чтобы упростить начертание формул, Эйнштейн опускает знак суммы, приняв раз навсегда, что если один и тот же значок встречается в выражении дважды, то по нему производится суммирование. Поэтому выражение для ds² можно записать просто

и это означает то же, что и вышеприведенная формула, содержащая знак суммы ∑.

В выражении для ds² величина dx_σ играет роль ковариантного вектора. Тогда величины g_στ (Эйнштейн в дальнейшем пишет g_μv) являются компонентами ковариантного тензора второго ранга, называемого "фундаментальным тензором". Из компонент фундаментального ковариантного тензора g_μv можно образовать компоненты контравариантного тензора g^μv. Для этого в определителе g = |g_μv| берут миноры, соответствующие элементу g_μv, и делят их на величину детерминанта g. Это и будут компоненты контравариантного фундаментального тензора g^μv. При этом

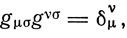
где δ^v_μ = 1 для v = μ и 0 для v ≠ μ. Далее произведение определителей обоих фундаментальных тензоров равно 1:

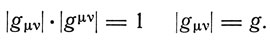
Детерминант преобразуется по закону

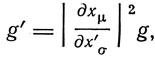
так что

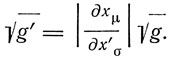
С другой стороны, четырехмерный объем

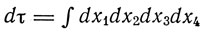
преобразуется по закону

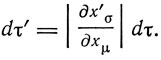
Откуда

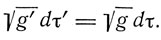
Вещественная величина √(-gdτ) является инвариантом. Этот инвариант "равен величине четырехмерного объема, измеренного в "местной координатной системе" посредством твердых масштабов и часов по принципам специальной теории относительности".

Поскольку ds - инвариант, то и экстремальная линия, проведенная между точками P₁ и Р₂ четырехмерного континуума, определяемая условием

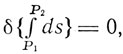
является инвариантом. Эту линию называют "геодезической". Ее уравнение имеет вид

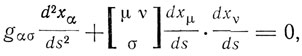
где 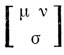- символ Кристоффеля, имеющий значение

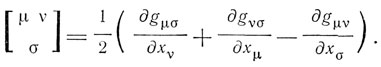
Отсюда получается уравнение геодезической линии в виде

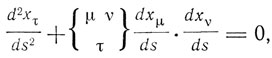
где по Кристоффелю

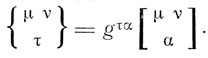
Важную роль в общей теории относительности играет тензор Римана-Кристоффеля, компоненты которого имеют вид

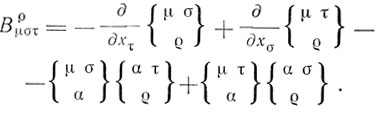
С помощью операции, известной под названием "свертки", из тензора четвертого ранга В^ρ_μστ получается ковариантный тензор второго ранга В_μτ, при этом

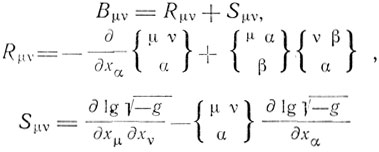
Уравнение движения материальной точки в произвольной системе отсчета Эйнштейн записывает в виде

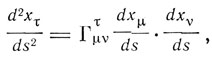
где 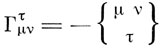- символ Кристоффеля. "Если все Г_μv^τ равны нулю, то точка двигается прямолинейно и равномерно; следовательно, эти величины обусловливают отклонение движения от прямолинейного и равномерного. Они являются компонентами гравитационного поля".

Эйнштейн различает "гравитационное поле" и "материю", относя к последней все, кроме гравитационного поля, в частности и электромагнитное поле. В свободном от материи гравитационном поле, по гипотезе Эйнштейна, должен обращаться в нуль тензор В_μv. Отсюда получаются уравнения поля

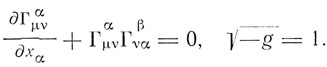
"Тот факт,- пишет Эйнштейн,- что эти уравнения, вытекающие из общего принципа относительности чисто математическим путем, в соединении с уравнением движения (в этом месте Эйнштейн ссылается на написанные выше уравнения движения) дают в первом приближении ньютоновский закон тяготения, а во втором приближении - объяснение открытого Леверье движения перигелия Меркурия (остающегося после внесения поправок на возмущение), должен, по нашему мнению, убедить в физической правильности теории".

Эти уравнения гравитационного поля в отсутствие материи соответствуют уравнению Лапласа в ньютоновской теории тяготения Δφ = 0.

Для того чтобы получить уравнения гравитационного поля в общем виде, которые должны соответствовать уравнению Пуассона Δφ = 4πχ, где χ - постоянная, - плотность масс, Эйнштейн вводит тензор материи и энергии Т_σ^α и псевдотензор энергии импульса t_σ^α. Он получает систему уравнений

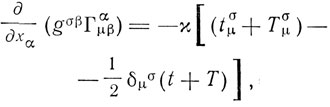
где Т_α^α = t. Отсюда получается система

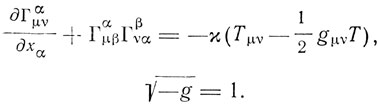
Эйнштейн замечает, что "введение тензора энергии материи не может быть обосновано одним только постулатом относительности" и что "самым сильным аргументом в пользу указанных уравнений является то, что из них следуют уравнения сохранения импульса и энергии для компонент полной энергии".

Из уравнений движения в первом приближении получается уравнение движения в теории Ньютона

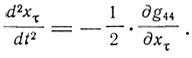
Здесь ^g₄₄/₂ играет роль гравитационного потенциала. Из уравнений поля тяготения в первом приближении получается уравнение Пуассона

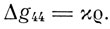
При этом гравитационный потенциал

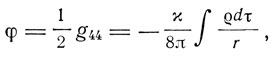
тогда как теория Ньютона при выборе единицы времени, в которой c = 1, дает

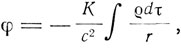
где К - гравитационная постоянная, равная 6,7*10^-8. Отсюда

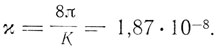
Далее Эйнштейн получает отклонение светового луча в гравитационном поле

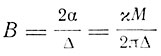
и вращение перигелия эллиптической орбиты планеты, которое за время полного периода равно

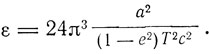
Здесь а - большая полуось орбиты, Т - период обращения планеты в секундах, с - скорость света в ^см/_сек, е - эксцентрицитет. Таково основное содержание основополагающей работы Эйнштейна по общей теории относительности.