Основные идеи теории Эйнштейна

Теперь Эйнштейн считал теорию настолько законченной и сформировавшейся, что уже через несколько месяцев после опубликования этой работы изложил основные идеи специальной и общей теории относительности в вышедшей в 1917 г. брошюре "О специальной и общей теории относительности". Предисловие к этой брошюре датировано декабрем 1916 г. Таким образом, она была написана в том же году, в каком вышла его фундаментальная работа по общей теории относительности. Она неразрывно связана с этой работой. "Автор,- пишет Эйнштейн в предисловии к своей брошюре,- приложил много усилий для того, чтобы достигнуть по возможности более ясного и простого изложения основных мыслей в той последовательности и связи, в какой они фактически возникли" (курсив мой.- П. К.). Вот почему нельзя обойти эту брошюру, излагая историю развития идей теории относительности. В ней с особой ясностью изложены идеи теории в том виде, как они сформировались к 1917 г.

Интересно, что первую часть брошюры, посвященную специальной теории относительности, Эйнштейн начинает с геометрии. В параграфе "Физическое содержание геометрических теорем" Эйнштейн со всей определенностью подчеркивает, что "геометрию следует рассматривать как область физики". "Истинность" геометрии доказывается опытом, в частности истинность эвклидовой геометрии доказывается опытом с твердыми телами. Установив такую "истинность" евклидовой геометрии, мы должны быть готовы к тому, что ее "истинность должна быть ограничена", как это выясняется в общей теории относительности.

Переходя к изложению основных понятий специальной теории относительности, Эйнштейн вводит понятие об инерциальной системе координат, .которую он называет "галилеевой".

"Систему координат, состояние движения которой таково, что относительно нее выполняется закон инерции, мы называем "галилеевой системой координат". Законы механики Галилея-Ньютона применимы только для галилеевой системы координат".

Начиная часть, посвященную общей теории относительности, Эйнштейн вновь подчеркивает связь специального принципа относительности с галилеевыми системами отсчета. Он говорит: "По отношению к К (галилеево тело отсчета) законы природы должны выражаться возможно проще. Но, кроме К, все тела отсчета К', которые движутся относительно К прямолинейно, равномерно и без вращения, совершенно эквивалентны К при формировании законов природы; все эти тела отсчета можно рассматривать как галилеевы. Справедливость принципа относительности предполагалась только для этих, но не для других (иначе движущихся) тел отсчета. В этом смысле мы говорим о специальном принципе относительности или о специальной теории относительности".

Отсюда - естественный переход к общему принципу относительности, под которым понимается утверждение, "что все тела отсчета К, К' и т. д. эквивалентны в отношении описания природы (формирования общих законов природы), каким бы ни было их состояние движения". Эйнштейн показывает далее роль принципа эквивалентности в утверждении этого общего принципа относительности.

Но поле тяготения влияет на масштабы и часы, и это делает невозможным описание процессов с помощью метода декартовых координат в любых не галилеевых системах отсчета. Здесь оказывается полезной гауссова идея криволинейных координат. Пространство "арифметизируется", т. е. каждой его точке сопоставляются четыре числа x₁, x₂, x₃, x₄, "которые не имеют никакого непосредственного физического смысла, но служат лишь для определенной, хотя и для произвольной нумерации точек континуума". Этот гауссов метод применим и к неевклидовому пространству, причем "описание пространственно-временного континуума в гауссовых координатах вполне заменяет описание с помощью тела отсчета". Это описание, как подчеркивает Эйнштейн, "не связано с евклидовым характером описываемого континуума, что также важно для общей теории относительности. Ведь, например, во вращающейся плоскости отношение длины окружности к диаметру не равно π, поскольку масштабы в направлении радиуса неизменны, а в направлении, касательном к окружности, испытывают лоренцево сокращение. Поэтому приведенная выше формулировка общего принципа относительности заменяется другой, более абстрактной: "Все гауссовы системы координат в принципе эквивалентны для формирования общих законов природы".

Чтобы конкретизировать эту абстрактную мысль, Эйнштейн прибегает к наглядным представлениям. Галилеева система отсчета специальной теории относительности может быть представлена твердым телом, по отношению к которому "изолированная" материальная точка находится в состоянии равномерного прямолинейного движения.

"Но в полях тяготения,- говорит Эйнштейн,- не существует твердых тел с евклидовыми свойствами; поэтому понятие твердого тела отсчета неприменимо в общей теории относительности. Гравитационные поля влияют и на ход часов, так что физическое определение времени непосредственно с помощью часов совершенно не обладает той степенью очевидности, какой оно обладает в специальной теории относительности?".

Поэтому система отсчета в общей теории относительности представляется деформируемым телом с нерегулярным ходом часов. "Это деформированное тело отсчета, которое не без основания можно назвать "моллюском отсчета", по существу, равноценно любой четырехмерной гауссовой системе координат. .. Общий принцип относительности требует, чтобы все эти моллюски могли быть использованы в качестве тел отсчета с одинаковым успехом при формировании общих законов природы; эти законы совершенно не должны зависеть от выбора моллюска".

Далее Эйнштейн набрасывает план получения общего закона гравитации. Исходят из галилеевой области, в которой не существует поля тяготения относительно галилеевой системы отсчета К. Эту область относят к любой системе отсчета или "моллюску отсчета" К!? В этой системе появляется гравитационное поле. G, которое может быть выведено путем преобразования координат. Следующий шаг заключается в нахождении общего закона гравитационного поля. Это обобщение получается из учета следующих требований:

• искомое обобщение должно также удовлетворять общему принципу относительности;
• если в рассматриваемой области имеется материя, то создаваемое ею гравитационное поле определяется только ее инертной массой и, следовательно... только ее энергией;
• гравитационное поле и материя вместе должны удовлетворять закону сохранения энергии (и импульса).

Эйнштейн указывает, что введенная в соответствии с этой программой теория гравитации "не только отличается своим изяществом, не только устраняет присущие классической механике недостатки... не только интерпретирует эмпирический закон равенства инертной и тяжелой масс", но и приводит к важным новым следствиям. К числу таких следствий относится искривление световых лучей в поле тяготения Солнца, объяснение движения перигелия Меркурия и смещение спектральных линий света больших звезд.

В заключение Эйнштейн останавливается на космологических проблемах. Он указывает, что представление о бесконечном в пространстве и времени мире несовместимо с законом тяготения Ньютона. Такой бесконечный мир обладал бы в среднем постоянной плотностью материи и, следовательно, приводил бы к возрастанию силы тяготения с расстоянием до бесконечно больших значений.

Поэтому теория Ньютона должна приводить к представлению об "островной Вселенной", в которой звездный мир представляет собой "конечный остров в бесконечном океане пространства". Эйнштейн считает это представление неудовлетворительным и указывает, что оно приводит к следствию, что свет, излучаемый звездами, а также отдельные звезды звездной системы должны непременно удаляться в бесконечность, никогда не возвращаясь и не вступая во взаимодействие с другими объектами природы. Такой мир, материя которого сконцентрирована в бесконечном пространстве, должен был бы медленно, но систематически опустошаться. Эйнштейн считает также неудовлетворительной попытку Зеелигера и др. спасти положение путем видоизменения закона Ньютона, указывая, что эти модификации закона тяготения "не имеют ни экспериментального, ни теоретического обоснования".

Эйнштейн останавливается на выдвинутой Риманом и Гельмгольцем концепции конечного и неограниченного пространства, в частности римановского сферического пространства, обладающего постоянной положительной кривизной. Обобщением такого пространства является эллиптическое пространство. Общая теория относительности делает весьма вероятным существование замкнутого неограниченного пространства с отличным от нуля радиусом кривизны.

Космологическим проблемам в свете общей теории относительности Эйнштейн посвятил опубликованную в том же, 1917 г. статью "Вопросы космологии и общая теория относительности". Указав, к каким трудностям приводит ньютоновская теория космоса, Эйнштейн пишет: "Я пришел к убеждению, что уравнения гравитационного поля, которых я до сих пор придерживался, нуждаются еще в некоторой модификации, чтобы на базе общей теории относительности избежать тех принципиальных трудностей, которые. .. были указаны для теории Ньютона". Эта модификация соответствует в теории Ньютона переходу от уравнения Пуассона вида

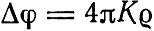
к уравнению

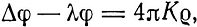
которому, в свою очередь, соответствует частное решение вида

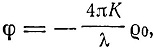
где - постоянная плотность материи. Точно так же в общей теории относительности от уравнений гравитационного поля

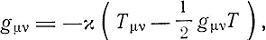
где

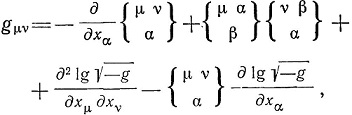
переходят к уравнению вида

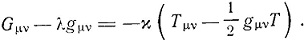
Эта постоянная λ оказывается равной

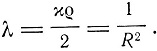
"Итак,- подводит Эйнштейн итог своим вычислениям,- вновь введенная универсальная константа λ определяется, если известна средняя плотность распределения Q, сохраняющаяся в состоянии равновесия, радиус R сферического пространства и его объем 2π²R³".

Таким образом, решение космической проблемы Эйнштейном приводит к стационарному конечному миру с положительной кривизной. Советский теоретик А. А. Фридман указал на возможность нестационарного решения, которое, как оказалось, соответствует реальным космологическим фактам (расширяющаяся вселенная Хэббла).

Таковы достижения Эйнштейна в области теории тяготения. Ему понадобилось десять лет напряженного труда и поисков, чтобы найти основы общей теории относительности и, тем самым, теории тяготения. Общая теория относительности принадлежит к числу замечательнейших достижений физики XX в. и оказала глубокое влияние на развитие теоретической физики, астрофизики и космологии нашего столетия. Ее создание определило и дальнейший научный путь самого Эйнштейна, путь мучительных поисков единой теории поля, единой физической картины мира, основанной на примате непрерывности. Грандиозная задача, которую поставил перед собой Эйнштейн, охватить математическими уравнениями всю вселенную, не увенчалась, да и не могла увенчаться успехом. Но она восхищает своей дерзновенной смелостью и несокрушимой верой в мощь человеческого разума.