Броуновское движение

В 1827 г. английский ботаник Броун открыл, что цветочная пыльца распадается в воде на мельчайшие частицы, находящиеся в непрерывном беспорядочном движении. Сначала он считал это явление присущим "первичным молекулам" живой материи, но потом обнаружил такое же движение "первичных молекул" и неорганических веществ. Открытие Броуна не сразу привлекло внимание исследователей и не сразу была понята его природа. Так, Реньо (1858) считал, что оно обусловлено неравномерным нагреванием раствора падающим светом, Джевонс полагал, что оно обусловлено электрическими силами. Но уже в 1863 г. Винер сделал заключение, что это движение "не может иметь причин ни в самих частичных, ни во внешних воздействиях на жидкость, а должно быть отнесено на счет внутренних движений, характерных для жидкого состояния". Последующие исследования, в особенности исследования Л. Гуи (1888), показали удивительное постоянство броуновского движения. Оно не меняет характера ни днем, ни ночью, ни в городе, ни в деревне и может длиться беспредельно. "Оно вечно и самопроизвольно" - так резюмирует Ж. Перрен итог многих исследований над броуновским движением. Все это укрепляло мысль, что броуновское движение представляет собой результат вечного теплового молекулярного движения среды, в которой взвешены броуновские частицы. Заслуга утверждения этой идеи в физике принадлежит Эйнштейну.

Научный путь Эйнштейна начался работами по молекулярной и статистической физике. В 1901 г. он опубликовал свою первую печатную работу "Следствия из явлений капиллярности". В следующем, 1902 г. была опубликована статья, носившая длинное название "О термодинамической теории разности потенциалов между металлами и полностью диссоциированными растворами их солей и об электрическом методе исследования молекулярных сил". В том же году Эйнштейн печатает статью "Кинетическая теория теплового равновесия и второго начала термодинамики". В следующем, 1903 г. он печатает работу "Теория основ термодинамики", и дополнение к этой работе под заглавием "К общей молекулярной теории теплоты" появляется в 1904 г., в том же году, в каком появилась упомянутая выше статья Смолуховского о флюктуациях. Вспоминая свой научный путь, семидесятилетний Эйнштейн писал об этих своих работах: "Не будучи знакомым с появившимися ранее исследованиями Больцмана и Гиббса, которые, по существу, исчерпывают вопрос, я развил статистическую механику и основанную на ней молекулярно-кинетическую теорию термодинамики. При этом главной моей целью было найти такие факты, которые возможно надежнее устанавливали бы существование атомов определенной конечной величины".

Есть что-то символическое в том обстоятельстве, что Эйнштейн, прежде чем подойти к теории броуновского движения, созданием которой он достиг намеченной им главной цели, самостоятельно и совершенно оригинально прошел путь, пройденный до начала XX в. Больцманом и Гиббсом. Этот путь привел его к доказательству существования броуновского движения, о наличии которого Эйнштейн до этого и не подозревал. Он продолжает свои заметки признанием в своем неведении: "Не зная, что наблюдения над "броуновским движением" давно известны, я открыл, что атомистическая теория приводит к существованию доступного наблюдению движения взвешенных микроскопических частиц".

Итак, броуновское движение было открыто дважды: в 1827 г. непосредственным наблюдением Броуном и в 1905 г. "на кончике пера" Эйнштейном. Сначала оно было открыто в известной степени случайно и природа его не была понята ни открывателем, ни последующими исследователями; затем, через 78 лет, оно было описано теоретически в результате углубленных занятий статистической и молекулярной физикой молодого служащего швейцарского бюро патентов.

30 апреля 1905 г. в Цюрихский университет была представлена докторская диссертация Альберта Эйнштейна "Новое определение размеров молекул", напечатанная в Берне. В 1906 г. она была перепечатана с исправлениями и дополнениями в 19-номере "Annalen der Physik". Эта работа была первой из цикла работ Эйнштейна по броуновскому движению, хотя в ней это движение даже не упоминается. Она была посвящена главной задаче, поставленной перед собой Эйнштейном: найти факты, "которые, возможно, надежнее устанавливали бы существование атомов определенной конечной величины". Эйнштейн ищет новый метод, с помощью которого можно было бы определять величину атомов. Все известные до этого методы базировались на кинетической теории газов. Эйнштейн показывает, что "величина молекул растворенного вещества в слабом недиссоциированном растворе может быть определена по внутреннему трению раствора и чистого растворителя и по диффузии растворенного вещества в растворителе, если объем молекулы растворенного вещества велик по сравнению с объемом молекулы растворителя". "Такого рода растворенная молекула,- добавляет Эйнштейн,- по своей подвижности в растворе и по влиянию на внутреннее трение последнего ведет себя подобно твердому телу, взвешенному в растворителе". Но именно так и ведут себя броуновские частицы и совершенно ясно, что Эйнштейн занимается по существу броуновским движением, не называя последнего.

Эйнштейн рассматривает задачу влияния взвешенного в жидкости очень малого шара на ее движение как чисто гидродинамическую задачу. Он показывает, что присутствие в жидкости многих беспорядочно распределенных малых шаров увеличивает ее коэффициент внутреннего трения на величину, пропорциональную отношению общего объема взвешенных шаров ко всему объему жидкости

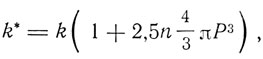
где k - коэффициент внутреннего трения жидкости, k^* - коэффициент внутреннего трения той же жидкости при наличии взвешенных шаров, n - число шаров (молекул), Р - эффективный гидродинамический радиус шара.

Далее, рассматривая диффузию растворенного недиссоциированного вещества в растворе, Эйнштейн находит соотношение

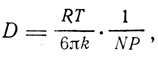
где R - газовая постоянная, Т - абсолютная температура, N - число молекул в грамм-молекуле, Р - эффективный гидродинамический радиус молекулы (частицы). Измеряя коэффициент внутреннего трения чистой жидкости и раствора, можно найти отношение

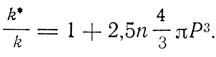
Но

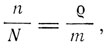
где - масса растворенного вещества в единице объема, m - его молекулярный вес. Таким образом,

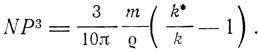
С другой стороны,

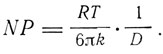
"Эти два уравнения,- пишет Эйнштейн,- дают нам возможность вычислить отдельно величины Р и N, из которых N не должна зависеть ни от природы растворенного вещества и растворителя, ни от температуры, если только наша теория соответствует действительности.

Эта диссертация, как уже говорилось, была перепечатана в 19-м томе "Annalen der Physik" с поправками и дополнением.

В журнальном тексте есть ссылка на статью 1905 г., опубликованную в том же знаменитом 17-м томе журнала, где были опубликованы работы по теории относительности и теории квант. Статья эта носит название "О движении взвешенных в покоящейся жидкости частиц, требуемом молекулярно-кинетической теорией теплоты". Таким образом, если в диссертации шла речь о методе определения размеров молекул и рассматривалось влияние взвешенных частиц на движение жидкости, то теперь речь идет уже о движении самих частиц в покоящейся жидкости. Эйнштейн в самом начале статьи пишет: "В этой работе будет показано, что согласно молекулярно-кинетической теории теплоты взвешенные в жидкости тела микроскопических размеров вследствие молекулярного теплового движения должны совершать движения такой величины, что легко могут быть обнаружены под микроскопом. Возможно,- добавляет Эйнштейн,- что рассматриваемые движения тождественны с так называемым броуновским молекулярным движением; однако доступные мне данные относительно последнего настолько неточны, что я не мог составить об этом определенного мнения".

В работе 1906 г. "К теории броуновского движения" Эйнштейн сообщает, что вскоре после появления этой работы 1905 г. Зидентопф из Вены сообщил ему, что он и другие физики пришли к выводу, что "так называемое броуновское движение вызывается беспорядочным тепловым движением молекул жидкости", как об этом думал еще Гуи в 1888 г. Однако Эйнштейн не ограничился качественной картиной движения, а подверг его количественному рассмотрению. Важнейшим его результатом был вывод, что средний квадрат смещения частицы за промежуток времени t пропорционален этому времени

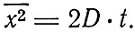
Как было показано им еще в диссертации и снова выведено в этой статье, коэффициент диффузии D равен

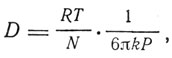
где k - коэффициент внутреннего трения, N - число Авогадро, R - газовая постоянная. Эйнштейн ясно видел, что его формула дает новый метод определения числа молекул и, следовательно, определения размеров атомов. "Если бы,- воскликнул Эйнштейн в конце своей статьи,- какому-либо исследователю удалось вскоре разрешить поднятые здесь важные для теории теплоты вопросы!"

В следующей работе - "К теории броуновского движения" (1906) - Эйнштейн обобщил и рассмотрел свой метод, распространив его не только на поступательное, но и на вращательное движение частиц. Для вращательного движения Эйнштейн нашел для среднего квадратичного поворота шарообразной частицы √Δr² формулу

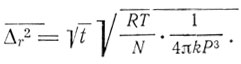
"Следовательно,- пишет Эйнштейн,- вращательное движение, вызываемое молекулярным движением, уменьшается с возрастанием Р гораздо быстрее, чем поступательное".

В том же, 1906 г. появилась статья М. Смолуховского "К кинетической теории броуновского молекулярного движения и суспензии", в которой он указывает, что полученные результаты "вполне согласуются с теми, которые я получил несколько лет тому назад и которые я считал с тех пор веским аргументом в пользу кинетической теории этого явления". Смолуховский указывает, что он хотел экспериментально проверить свои выводы, но это ему не удалось. Работы Эйнштейна заставили его опубликовать свои теоретические соображения. Свой метод Смолуховский считает более простым и потому более убедительным, чем метод Эйнштейна. Смолуховский получает ту же формулу для среднего квадрата смещения частицы, что и Эйнштейн, ко с другим коэффициентом. Как и Эйнштейн, Смолуховский приходит к выводу, что "частицы, взвешенные в жидкой или газообразной среде, держат себя так, как если бы они были самостоятельными молекулами с нормальной кинетической энергией, но соответственно с гораздо меньшей длиной свободного пути". Работы Эйнштейна и Смолуховского настоятельно требовали экспериментальной проверки. Такой эксперимент позволил бы заглянуть внутрь молекулярного мира и определить недоступные прямому определению молекулярные величины. Отсюда видно огромное принципиальное значение таких опытов. Заслугой французского физика Жана Перрена и является постановка этих важных экспериментов. Они были начаты в 1908 г. и продолжались в течение ряда лет. Результаты их были изложены в ряде статей и в книге Перрена "Атомы", получившей широкую популярность, неоднократно переиздававшейся и переводившейся на иностранные языки, в том числе и на русский. На русском языке появился также доклад Перрена "Броуновское движение и молекулы", сделанный им во Французском физическом обществе 15 апреля 1909 г.

Ж. Перрен

Перрен, прежде всего, хочет доказать, что к броуновским частицам применимы основные положения кинетической теории газов: закон равномерного распределения энергии по степеням свободы, распределение Больцмана. Непосредственное измерение скорости движения броуновской частицы приводит к неверному выводу, что кинетическая энергия частицы составляет примерно стотысячную долю средней кинетической энергии молекул. Перрен указывает, что такое непосредственное определение скорости частицы неправильно, ни кажущаяся траектория частицы, ни ее кажущаяся скорость не имеют ничего общего с действительным движением частицы. "Кажущаяся средняя скорость зернышка в течение данного промежутка времени "прямо безумно" варьирует и по величине и по направлению и при этом нисколько не обнаруживает стремления к какому-либо определенному пределу". Кинематографические снимки движения, сделанные Виктором Анри, показывают, что траектория движения не имеет касательной. "Таким образом, в этом явлении мы встречаемся с одним из тех случаев, когда нельзя не подумать о функциях, не имеющих производной,- функциях, которые не нужно было бы рассматривать, как простые математические курьезы, ибо природа подсказывает их так же, как и функции, имеющие производную".

Поэтому для изучения явления надлежит прибегнуть к статистическим методам. Перрен, изготовив однородную эмульсию с одинаковыми зернышками, рассматривал распределение частиц по высоте. Он определил сначала плотность частиц. Для зерен гуммигута при 20° С такая плотность оказалась 0,207, для мастики - 0,063. Затем он определял радиус частиц, наблюдая скорость падения и применяя закон Стокса. Для проверки он считал непосредственно зерна и измерял длину цепочки из таких зерен. Он нашел, что радиусы частиц колебались от 0,52 μ до 0,14 μ. Затем он наблюдал в микроскоп распределение частиц по высоте. Так, для зерен гуммигута радиусом 0,212 μ он делал подсчеты в четырех слоях, отстоящих по вертикали один от другого на расстояниях

Наблюденные 13 000 зернышек распределились по этим высотам так, что их соответствующие концентрации относились, как числа

которые практически совпадают с числами

полученными по показательному закону. "Итак,- заключает Перрен,- распределение зерен имеет именно такую же форму, как и распределение весомого газа в состоянии равновесия".

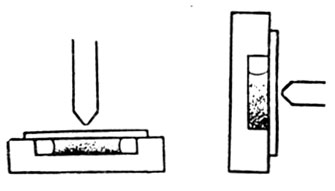
Метод наблюдения распределения частиц по высоте

Тщательные опыты подобного рода привели Перрена к важному выводу: "Законы идеальных газов, распространенные уже вант Гоффом на разведенные растворы, распространяются, стало быть, и на однородные эмульсии, и молекулярную теорию броуновского движения можно считать надежно обоснованной; вместе с тем становится крайне трудно отрицать объективную реальность молекул".

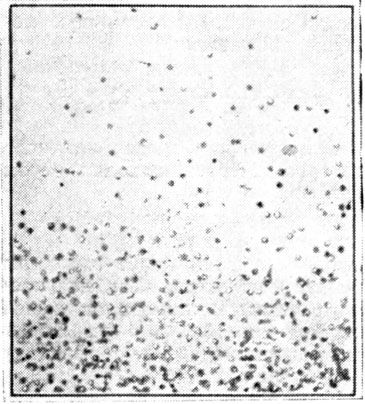
Распределение частиц по высота

Произведя "особенно тщательные измерения" с зернами радиуса 0,22 μ, Перрен получил из барометрического закона число Авогадро. Значение, данное Перреном,

Отсюда он находит постоянную молекулярной энергии

Разделив число Фарадея на число Авогадро, Перрен находит заряд электрона

Перрен вычислил далее диаметры молекул и их массы. Так, для массы молекулы кислорода он нашел значение 45,4*10^-24 г, а для массы атома водорода - величину 1,43*10^-24 г.

Рисунок Перрена 'траектории' броуновских частиц

Перрен проверил и закон Эйнштейна. Он показал его справедливость как для поступательного, так и вращательного движения. Рисунок Перрена зигзагообразных движений трех броуновских частиц вошел в учебники. В заключение своего доклада Перрен дает сводку полученных до 1908 г. измерений молекулярных величин. "Данные этой таблицы,- пишет Перрен,- образуют в своем целом самое прочное основание для того, что могло бы быть названо принципом молекулярной реальности" (см. таблицу).

Вслед за наблюдением броуновского движения в жидкостях начались и наблюдения в газах. Смолуховский в упомянутой выше работе вычислил среднее смещение броуновской частицы с радиусом а = 10^-4 см в воздухе. Принимая для числа молекул в 1 см³ значение 4*10¹⁹, он нашел для Δ = 1,4*10^-3 см. Смолуховский указал на наблюдения Бодашевского (1881-1882) броуновского движения частиц дыма. В 1907 г. броуновское движение в газе без количественного анализа наблюдал Эренгафт.

В 1908 г. М. де Бройль наблюдал движение частиц металлической пыли, распыляемой при горении электрической дуги. Пропуская эти частицы между пластинами вертикального конденсатора, де Бройль обнаружил, что часть этих частиц заряжена положительно, часть - отрицательно. В 1909 г. де Бройль произвел количественные наблюдения движения капелек воды, сконденсированных на частицах дыма. Де Бройль наблюдал движение этих капелек в горизонтальном электрическом поле (вертикальный конденсатор). Скорость движения определялась из уравнения

где F - напряженность поля, k - коэффициент трения. Далее определялось Δx², и из уравнения Эйнштейна

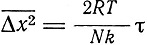
определялось k. Тогда, подставив N из данных Перрена, Де Бройль определял e. Наименьшее значение, полученное им, было e = 4,5*10^-10.

В 1910 г. Милликен со своими сотрудниками предпринял исследование броуновского движения в газах. Результаты этого исследования были им опубликованы в 1911 г. и более подробно Флетчером в том же году. Милликен комбинировал найденный им закон падения капли в электрическом поле с уравнением Эйнштейна, откуда получал значение Ne независимо от размера частиц и сопротивления среды. Милликен и Флетчер нашли, что Ne = 2,88*10¹⁴ электростатических единиц, тогда как из электролиза следует, что Ne = 2,896*10¹⁴. "Эта работа,- заключает Милликен,- доказывает справедливость уравнения Эйнштейна с гораздо большей точностью, чем было достигнуто в прежних работах по Броуновскому движению, и с минимумом допущений".

Таким образом, теория броуновского движения дала возможность экспериментального подтверждения основ молекулярной физики. Но она также доказала справедливость основной идеи статистической теории: сочетания регулярных законов механики с принципами теории вероятностей, что дало возможность статистической интерпретации второго начала. Второе начало оказалось статистическим законом, и броуновское движение продемонстрировало возможность статистических отклонений от равновесного состояния. В своем докладе 1913 г. в Геттингене (о геттингенских докладах нам неоднократно придется говорить в дальнейшем) М. Смолуховский говорил по этому поводу: "Если второе начало в одной из своих форм, как например "теплота не может сама собою переходить от более холодного тела к более нагретому", или "круговой процесс, при котором совершалась бы работа за счет теплоты тела более низкой температуры невозможен", или "энтропия замкнутой системы с течением времени может только возрастать" верно, то здесь несомненно противоречие с атомистически-кинетической теорией, требующей принципиальной обратимости всех процессов. Больцман, как известно, пытался все же доказать, что по кинетической теории процессы должны были бы вообще протекать в согласии с термодинамикой и что ожидаемые теоретические исключения из этого благодаря своей ничтожной вероятности были бы вообще незаметны; с другой же стороны, феноменологи отвергают абсолютную правильность кинетической теории. В настоящее время уже доказано, что в действительности существует целый ряд микроявлений, экспериментально легко наблюдаемых (как, например, броуновское молекулярное движение, явления опалесценции в эмульсиях), основанных как раз на том, что истинное состояние заметно отклоняется от термодинамики ожидаемого "нормального равновесия". Таким образом, абсолютное значение законов термодинамики опровергается опытом и точка зрения догматической термодинамики становится неосновательной. Насколько все-таки эту последнюю следует считать приближенно справедливой, можно судить в настоящее время лишь с точки зрения статистической механики Максвелла-Больцмана-Гиббса, получившей в вышеназванных явлениях осязаемое подтверждение, а частично и дальнейшее развитие".

Успехи атомистики были неразрывно связаны с успехами и развитием статистического метода. Но классическая статистика Больцмана-Гиббса испытала судьбу всех классических теорий: в явлениях излучения она получила, с одной стороны, новое поле применения и, с другой стороны, натолкнулась на непреодолимые противоречия. В дальнейшем нам придется говорить об этом более подробно. Тем не менее одним из наиболее значительных результатов развития физики в первом десятилетии XX в. является победа классической статистики Больцмана-Гиббса и атомной теории вообще. Отмечая этот факт на съезде естествоиспытателей в Кенигсберге в 1910 г., М. Планк говорил: "Даже в границах самой термодинамики, в области состояний равновесия и стационарных состояний, кинетическая теория пролила свет на ряд вопросов, которые должны были оставаться неясными для чистой термодинамики... Объяснив так называемое броуновское молекулярное движение, она дала непосредственное и, так сказать, осязательное доказательство своей обоснованности и необходимости и, таким образом, одержала одну из величайших своих побед. Подводя итоги, можно сказать: в области учения о теплоте, химии и теории электронов кинетическая атомистика является уже не рабочей гипотезой, а прочно и надолго обоснованной теорией".