Квантовая теория в 1910-1913 годах

Следующим этапом развития квантовой теории является период 1910-1913 гг. В этот период выявляется универсальное значение постоянной Планка, чему в особенности способствовали фундаментальные исследования школы Нернста в области низких температур. Другой особенностью этого периода является проникновение идеи квантов в спектроскопию и теорию атома. Это проникновение завершилось основополагающей работой Н. Бора 1913 г.

Рассмотрение этого периода удобно начать с обзорной работы Г. А. Лоренца. 17 апреля 1909 г. Лоренц выступил на 12-м съезде голландских естествоиспытателей и врачей с докладом "Гипотеза световых квантов". Доклад этот был опубликован в 1910 г. в немецком переводе Баркгаузена. Пояснив в начале своего доклада основные идеи вывода формулы Планка, Лоренц далее пишет: "Удовлетворительный результат, полученный Планком в теории излучения с помощью его гипотезы, вынудил различных исследователей прийти к представлению, что вообще возникновение света и его превращение в другие формы всегда осуществляется посредством конечных световых квантов, имеющих указанную Планком величину и существующих самостоятельно".

Сформулировав, таким образом, гипотезу световых квантов как своеобразных световых частичек, Лоренц упоминает в этой связи уже рассмотренную нами основополагающую работу Эйнштейна. Приведя примеры, подтверждающие гипотезу Эйнштейна (фотоэффект, люминесценция, явления в каналовых лучах, наблюдаемые Штарком в 1908 г.), Лоренц пишет: "Все это, без сомнения, весьма замечательно, но, несмотря на это, мне кажется, что при более детальном анализе возникают серьезные возражения против гипотезы световых квантов".

Из этих возражений Лоренц, прежде всего, приводит возражения, связанные с физиологией зрения. В 1906 г. Крис наблюдал наиболее слабые световые раздражения, еще воспринимаемые глазом. Из этих опытов, как указывает Лоренц, вытекало, что "зеленые лучи, которые попадали в глаза только на короткое время, могли вызвать световые ощущения, когда на сетчатку в целом падало от 30 до 60 световых квантов, тогда как при длительном освещении для светового ощущения требуется примерно 140 квантов в секунду".

Интересно, что в 30-х годах С. И. Вавилов, наблюдая флюктуации кратковременных световых потоков, наблюдаемых глазом, нашел, что в среднем глаз воспринимает 25 фотонов, соответствующих λ = 510 μ при кратковременных вспышках. Свои наблюдения флюктуации световых потоков Вавилов рассматривал как одно из важнейших доказательств квантовой природы излучения. Лоренц в 1909 г. полагал, что такое малое число световых квантов, воспринимаемых глазом, вряд ли способно вызвать такие сложные процессы, которые происходят на сетчатке при восприятии ею светового раздражения. Опыты Криса он рассматривал как одно из возражений против гипотезы световых квантов. Но Лоренц соглашается, что судить о процессах на сетчатке трудно, и переходит к другим возражениям, которые он считает "более весомыми".

Из факта интерференции при больших разностях хода, которая для "однородного" света составляет около двух миллионов волн, следует, что "в каждом световом кванте следуют друг за другом, по крайней мере, два миллиона световых волн и что, таким образом, если положить длину волны равной 4*10^-5 см, каждый квант распространяется в направлении движения на область по меньшей мере в 80 см".

Лоренц очень ясно представляет, что отдельные кванты независимы друг от друга и не могут давать интерференции, интерферирует один квант сам с собой. Поэтому если представлять его себе как некоторое волновое образование, то он согласно приведенному подсчету должен иметь в продольном направлении протяжение порядка нескольких десятков сантиметров и даже метра. Отсюда вытекает следующая трудность. Молекулы вещества могут поглощать световую энергию только целыми квантами. Как она (молекула) может решить, когда к ней подходит первая волна, следует ли начать поглощение или нет, доставит ли цуг достаточное количество волн, чтобы образовать квант? "Должно представлять, что частица заранее поглощает энергию, чтобы ее сохранять до тех пор, пока не накопится целый квант и отдаст эту энергию обратно, если ей не посчастливится накопить целый квант".

Далее Лоренц указывает, что квант должен иметь и значительные поперечные размеры. Исследуя действие телескопа при наличии диафрагмы и без нее и учитывая, что часто кванты не наблюдаемы, Лоренц приходит к заключению, что поверхность светового кванта должна иметь порядок многих сотен квадратных сантиметров. Но поскольку звезда видима и невооруженным глазом, то в зрачок проникнет очень малая часть кванта. А так как сетчатка воспринимает только целые кванты, то в глазе каким-то образом дробные части вновь объединяются в целые кванты. "Сказанное может быть достаточным,- заключает Лоренц,- чтобы показать, что о световых квантах, неделимых и сконцентрированных в малых объемах, не может быть и речи".

Эти же возражения Лоренц повторяет и в цикле докладов, прочитанных в 1910 г. под общим названием "Старые и новые вопросы физики". Эти доклады были прореферированы М. Борном, реферат которого был опубликован в том же, 1910 г. в журнале "Physikalische Zeitschrift". Большая часть реферата посвящена вопросу об эфире и теории относительности, но в последних двух докладах речь идет о теории квантов. Лоренц указывает, прежде всего, на трудность применения теоремы равномерного распределения энергии по степеням свободы к равновесному излучению. Эфир обладает бесконечным числом степеней свободы, и, соприкасаясь с материей, он должен, так сказать, "перекачать" в себя всю ее энергию, так что температура весомых тел при равновесии должна равняться абсолютному нулю. Так как это невозможно, то, очевидно, в природе при равновесии должно быть конечное соотношение между энергиями эфира и материи, что указывает на необходимость введения новой гипотезы. Такая гипотеза и была сделана Планком при выводе формулы излучения, в виде идеи квантов энергии. Лоренц указывает, что Эйнштейн и Штарк пошли дальше Планка и приписали квантам энергии "самостоятельное существование в эфире". Этим предположением удалось объяснить фотоэлектрический эффект.

Но здесь же Лоренц обращает внимание на трудности квантовых представлений и повторяет свои возражения против квантовой гипотезы.

"Хотя Лоренц,- писал в своем реферате Борн,- не мог оспаривать эвристической ценности этой гипотезы, все же он защищал старые теории так долго, сколько было возможно".

Далее Лоренц в своих докладах напоминал о теории Д. Д. Томсона, согласно которой волновой фронт является неравномерным, поскольку энергия сосредоточена в отдельных местах ("пятна света"). Квантовые представления подтверждаются теми явлениями, в которых кажется, что производимый эффект производится в отдельных точках конечными порциями энергии. Лоренц ставит вопрос: могут ли обычные пучки света, не состоящие из квантов, отдавать электрону конечную порцию энергии, равную величине элемента энергии? Проведенный им расчет показывает, что для обычных световых пучков электрон не может получить света, достаточного для кванта энергии. Чтобы электрон мог накопить свет, равный такому кванту, требуется чрезвычайно большое время. Общий вывод Лоренца из проведенного им исследования заключается в том, что объяснение целого ряда явлений без допущения световых квантов представляет большие трудности.

Лоренц упоминает также о гипотезе Эриха Гааза, который использовал модель атома Томсона и представления Ленарда о фосфоресценции, согласно которым свет выбрасывает электрон из молекул и свечение молекулы возникает при возвращении электрона. Можно рассчитать энергию, необходимую для отрыва электрона из атома Томсона, и отсюда определить порядок h. У Гааза получилось h = 4,0*10^-27, что по порядку величины совпадает с постоянной Планка. Но гипотеза Гааза также наталкивается на значительные трудности. Тем не менее в этой гипотезе мы встречаем первую попытку связать квантовый характер излучения со структурой атома.

Последнюю, шестую лекцию Лоренц посвящает выводу формулы Планка. Его вывод, основанный на идеях статистики Больцмана и Гиббса, несколько отличается от вывода Планка. Применяя статистику Больцмана, Лоренц рассматривает равновесие между молекулами и резонаторами Планка. Он находит, что в равновесном состоянии средняя энергия молекулы равна 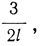а резонатора Планка 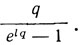Из классической статистики следует, что средняя энергия одноатомной молекулы равна 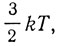откуда постоянная

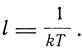
Величина q у Лоренца играет роль элемента энергии, и, полагая ее пропорциональной частоте v (q = hv), Лоренц приходит к формуле Планка для средней энергии осциллятора

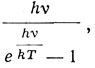
Лоренц не отрицает наличия определенного произвола в своем выводе. Придуманная им модель лотереи, иллюстрирующая статистические отношения в системе из молекул газа и осцилляторов Планка, теоретически не обоснована и является временным средством, обусловленным тем, что действительные процессы обмена энергией между молекулами и резонаторами неизвестны.

Но Лоренц дает другой вывод, основанный на статистической механике Гиббса. Применяя статистику Гиббса к системе, состоящей из весомых молекул и резонаторов частоты v, он принимает для распределения выражение

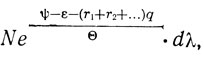
где ε - энергия только весомых молекул, а r₁, r₂,... числа элементов энергии q, приходящиеся на различные сорта резонаторов. Вычисление средней энергии молекул и резонаторов опять приводит к формуле Планка.

Лоренц заканчивает свою работу словами: "Будущему остается еще разрешить много загадок".

Пока же загадки теории квант продолжали волновать ученых. 3 февраля 1911 г., через два с небольшим месяца после лекций Лоренца Планк делает новый доклад в Немецком физическом обществе в Берлине, в том самом Обществе, где в 1900 г. он сделал свой исторический доклад о черном излучении. С воспоминания об этом он начал свой новый доклад.

"Десять с лишним лет тому назад, - говорил Планк, - я имел честь развить в этом самом месте основные черты теории теплового излучения, к которым также относилась существенная гипотеза о том, что в возникновении лучистой теплоты играют определенную своеобразную роль некоторые конечные, неделимые кванты или элементы энергии величиной hv". Планк указывал далее, что эта гипотеза противоречила представлениям электродинамики и электронной теории, но оказалась полезной в ряде исследований, из которых он особенно подчеркивает исследования Эйнштейна и Нернста об удельной теплоемкости твердых и жидких тел. Все это, по мнению Планка, заставляет "идти дальше", с тем чтобы "сколько-нибудь рассеять густой туман, еще до сих пор висящий над квантами энергии".

Основной целью длительных поисков Планка было примирение гипотезы квантов с положениями максвелловской электродинамики. Эти поиски, как он признается сам, особенно стимулировала изложенная выше статья Лоренца, в которой очень выпукло были показаны трудности наглядного "классического" представления кванта энергии. Для Планка труднейшим вопросом квантовой гипотезы был вопрос о непрерывном поглощении осциллятором падающей на него энергии. "Как можно,- спрашивал Планк,- реализовать такой осциллятор, чтобы он при облучении его тепловыми лучами, воспринимал только один элемент энергии? Он ведь должен поглощать его из падающего на него возбуждающего излучения и притом всю величину кванта сразу. Если поэтому возбуждающее излучение, которое, конечно, может иметь любую малую интенсивность, будет слабым, то осциллятор вообще ничего не поглощает".

Интересно наблюдать в этих сомнениях Планка абсолютную убежденность в справедливости классических представлений об излучении. Он может представить себе осциллятор, поглощающий и излучающий энергию непрерывно, но представить излучение с прерывной структурой, с конечной интенсивностью не ниже определенного предела он еще не может. Он допускает возможность квантового "порога раздражения" у осциллятора, идея которого, как он отмечает в своем докладе, была высказана в 1909 г. Рейнганумом, но он не может допустить квантового порога интенсивности излучения. Вместе с тем допущение квантового порога раздражения, ниже которого осциллятор вообще не способен поглощать энергию, не устраняет трудностей со временем поглощения, которые для квантов высокой частоты должны быть очень большими. Все эти трудности заставляют Планка принять новую гипотезу, что процесс поглощения энергии осциллятором следует считать непрерывным, подчиняющимся законам классической электродинамики. Излучение же осциллятора предполагается совершающимся прерывно, определенными квантами энергии ε = hv. Обрабатывая эту идею математически, Планк получает для средней энергии осциллятора выражение

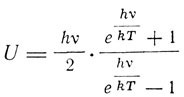
вместо прежнего значения 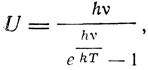причем выражение для плотности энергии излучения выражается прежней формулой Планка. Таким образом, новая гипотеза не приводит к новым выводам относительно законов черного излучения, но приводит к новому выражению для энергии осциллятора. Эта энергия для абсолютного нуля уже не будет равняться, как раньше, нулю, а будет равняться конечному значению ^hv/₂. "Эта остаточная энергия сохраняется в среднем у осциллятора и при абсолютном нуле температуры. Он не может ее потерять, поскольку он вообще не излучает никакой энергии, если U меньше ^hv/₂". Так вошла в физику идея нулевой энергии. Это, конечно, существенный результат, хотя Планк и указывает, что измерения теплоемкости для низких температур, предпринятые Нернстом и его учениками, недостаточны для проверки выражения энергии осциллятора. Но, обсуждая возможные пути проверки своей гипотезы о независимом характере процессов поглощения и излучения, Планк делает несколько интересных замечаний. Он считает, например, что при бомбардировке осциллятора электронами он будет сообщать этим электронам определенную скорость, зависящую от частоты осциллятора v, и что, возможно, этим объясняется отсутствие вклада "свободных" электронов в теплоемкость металла. Планк высказывает идею, что и радиоактивные излучения обусловлены квантовыми процессами, указывая, в частности, на определенную скорость α-частиц, хотя квантовый механизм радиоактивных процессов должен отличаться от тех колебаний, которые обусловливают и температуру, и теплоемкость тела. Планк заканчивает свой доклад утверждением, что, хотя новая гипотеза еще не уясняет законов случая, все же идея квант способна привести в связь многие физические явления и поэтому не может быть отвергнута.

1911-й год вообще был очень важным для развития квантовой теории. Теория квант со всей силой зазвучала на 83-м съезде немецких естествоиспытателей и врачей в Карлсруэ, где 25 сентября 1911 г. были заслушаны доклады Ф. Газенорля и А. Зоммерфельда, посвященные проблемам теории квантов. Через месяц после этого съезда в Брюсселе состоялся первый Соль-веевский конгресс, посвященный теме "Излучение и кванты".

Доклад Ф. Газенорля "Об основах механической теории тепла" любопытен тем, что в нем содержалась первая попытка квантового истолкования серии Бальмера. Газе-норль начинает с больцмановского вероятностного определения энтропии, которое, по его мнению, трудно применять в связи с необходимостью гипотез о молекулярной структуре тел. Поэтому Газенорль кладет в основу своих рассуждений каноническую совокупность Больцмана- Гиббса. Отсюда Газенорль переходит к исследованиям Планка по тепловому излучению и получает его формулу для энергии и энтропии осциллятора. Газенорль упоминает также и о результатах Эйнштейна в теории теплоемкости твердых тел. Все это приводит к выводу, что гипотеза Планка в высшей степени полезная рабочая гипотеза и что поэтому пока не следует ставить вопроса о законности такой гипотезы, а попытаться проследить все возможные следствия этой гипотезы. Газенорль поднимает вопрос обобщения теории Планка на случай резонаторов, период колебания которых будет зависеть от энергии (несинусоидальные процессы). Он предполагает, что и в этом общем случае фазовое пространство подразделяется, как и в случае план-ковского осциллятора, на равновеликие области h, ограниченные кривыми постоянной энергии. Он полагает по Планку фазовый объем равным v = τ*dE, где τ - период колебания, являющийся в общем случае функцией энергии. Проведя в фазовой плоскости кривые

он полагает части фазовой плоскости между этими кривыми одинаковыми и равными постоянной Планка h:

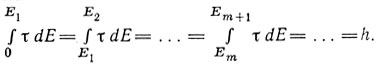
Газенорль полагает, что энергия осциллятора может принимать только дискретные значения 0, E₁, E₂, ..., которые теперь не являются кратными "кванта энергии", как в случае линейного осциллятора Планка. Периоды колебаний теперь будут также иметь дискретные значения τ₁ = τ(E₁), τ₂ = τ(E₂), ... Эти значения определяются величиной фазового элемента h и видом функции τ(E). Газенорль ставит вопрос; какова должна быть связь между энергией и периодом колебания, чтобы получилась серия Бальмера? Эту связь он изображает графически в виде кривой, изображающей зависимость Е от τ. Для малых значений энергии τ имеет постоянное значение А, затем период очень медленно растет с увеличением энергии. Возрастание периода с энергией постепенно начинает убыстряться и при приближении энергии к предельному значению E₁ период будет бесконечным. Газенорль иллюстрирует это поведение осциллятора примером движения тяжелой точки в потенциальной яме. Энергия Е соответствует отрыву электрона из атома, а в модели с потенциальной ямой - выбросу точки на край ямы. Для двух последовательных периодов τ_m и τ_m+1 должно удовлетворяться условие

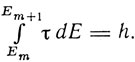
Отсюда при данной зависимости τ от E Газенорль получает формулу Бальмера

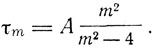
При этом последовательные значения энергии у него имеют вид

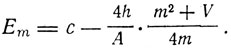
Сам Газенорль замечает, что нет ничего удивительного в том, что подходящим выбором функции τ(E) можно получить частоты серии Бальмера. Он полагает, что при соответствующих функциях τ(E) можно получить любые сериальные законы, вроде законов Ридберга. Эта гибкость, или, как выражается Газенорль, "растяжимость", теории позволяет описать сложные спектры, не прибегая к.сложным гипотезам о структуре излучателя. Вместе с тем теория Газенорля исходит из гипотезы Планка о дискретных значениях энергии осциллятора. Сам Газенорль признает, что его теория не может претендовать на знание теории закономерности спектров. Он рассматривает ее как пример возможного обобщения гипотезы Планка. Конечно, теория Газенорля неудовлетворительна и не получила дальнейшего развития. Но как первая попытка квантовой интерпретации спектральных закономерностей, как первая попытка связать частоты колебаний с формой энергетических кривых она, несомненно, заслуживает внимания.

Того же 25 сентября 1911 г., когда Газенорль делал свой доклад, выступил с докладом "Квант действия Планка и его общее значение в молекулярной физике" А. Зоммерфельд. В начале своего доклада (названного самим автором рефератом) Зоммерфельд указывает, что ему было сделано предложение выступить на съезде с докладом об относительности. На это Зоммерфельд ответил, что теория относительности уже стала прочным достоянием физики и поэтому перестала быть актуальной проблемой физики.

Это очень характерное замечание. За шесть лет, прошедших с момента создания теории относительности, ведущие физики уже стали рассматривать ее как классическую, прочно утвердившуюся в физике теорию. Иная судьба постигла теорию квантов. Хотя квантовая гипотеза была старше теории относительности на пять лет, она отнюдь не стала ясной и законченной. "Здесь основные понятия находятся в движении и проблемы неисчислимы",- говорил Зоммерфельд. Упомянув о том, что создатель теории Планк меняет свою первоначальную точку зрения, что Эйнштейн и Нернст расширили область применения теории квантов, Зоммерфельд продолжал. "Ничто не может быть насущнее для современной физики, чем выяснение взглядов на этот вопрос. Здесь находится ключ ситуации, ключ не только для теории излучения, но и для молекулярной структуры материи, и этот ключ сегодня еще далеко запрятан".

Таким образом, Зоммерфельду стало ясно, что гипотеза квантов является не только ключом для теории излучения, но и ключом к атомной физике (Зоммерфельд говорит о "молекулярной" теории, имея в виду атомную теорию).

Рассматривая далее в своем докладе проблему излучения, Зоммерфельд указывает, что все попытки рассматривать проблему излучения с классических позиций неизбежно приводят к неверному закону Рэ-лея-Джинса. Необходимо отказаться от теоремы равномерного распределения энергии по степеням свободы. В связи с этим Зоммерфельд излагает только что предложенный Нернстом вывод формулы Планка. В выводе Нернста средняя энергия осциллятора вычисляется не по теореме равномерного распределения энергии по степеням свободы, а в предположении наличия дискретных порций энергии. Из общего числа N осцилляторов N₀ обладают энергией 0, N₁ - энергией ε, N₂ - энергией 2ε и т. д. При этом числа N₀, N₁, N₂, ... определяются по статистике Больцмана:

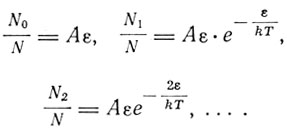
Так как 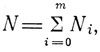то 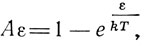средняя энергия осциллятора

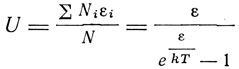
вместо kT по классической теории.

Используя получаемое из электродинамики соотношение между средней энергией осциллятора и объемной плотностью энергии излучения

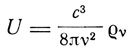
и полагая ε = hv, получим формулу Планка:

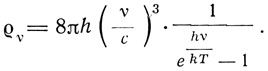
"Простота и красота этих рассуждений,- замечает Зоммерфельд,- не может, однако, скрыть от нас исключительных трудностей, лежащих в их основании". Трудность эта заключается в противоречии между формулой, выражающей зависимость энергии осциллятора от энергии излучения, и гипотезой квантов энергии. Формула, связывающая U и _v основана на представлении непрерывного обмена энергией между излучением и осциллятором, а выражение для U основано на гипотезе поглощения и излучения энергии осциллятора квантами.

Затем Зоммерфельд останавливается на трудностях в классической теории теплоемкости. В классической теории теплоемкости принцип равномерного распределения энергии привел к блестящим результатам, а именно правильному отношению теплоемкостей для одноатомных и двухатомных газов и закону Дюлонга и Пти для твердых тел. "Это, конечно, светлая сторона картины, которую нельзя представить иначе, как светлую",- говорит Зоммерфельд и переходит к "облакам" картины, заимствуя это выражение из знаменитой балтиморской лекции Томсона (Кельвина), Таким "облаком" является зависимость теплоемкости твердых тел от температуры... "Перед этим фактом,- как заметил Нернст,- теперешняя механика тепла совершенно беспомощна".

Эти трудности были в сильной степени смягчены теорией Эйнштейна. Формула Эйнштейна заменяет классическое выражение для энергии грамм-молекулы твердого тела U = 3RT выражением

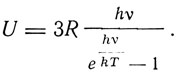
Это выражение получается при замене равномерного распределения энергии по степеням свободы распределением Планка. При этом предполагается, что все молекулы твердого тела колеблются независимо друг от друга с одной и той же частотой. В том же, 1907 г., в каком появилась статья Эйнштейна, Нернст прочитал силимэновскую лекцию, в которой указывал, что атомные теплоемкости твердых тел при низких температурах становятся крайне малыми. Этот результат вытекает из формулы Эйнштейна, причем он сам смог проиллюстрировать на алмазе справедливость закона зависимости теплоемкости от температуры даваемой его формулой. Тщательные исследования, проводимые Нернстом и его сотрудниками в лаборатории физико-химического института Берлинского университета, показали, однако, что количественное совпадение формулы Эйнштейна с опытными данными не вполне удовлетворительно. В 1911 г. Нернст и Линдеман предложили эмпирическую формулу

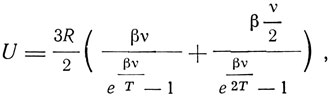
где β = ^h/_k. Но уже в следующем, 1912 г. Дебай нашел теоретически более точную формулу, чем формула Эйнштейна и Нернста и Линдемана.

Говоря о работах лаборатории Нернста, Зоммерфельд сравнивает их начение для квантовой теории со значением работ по черному излучению, проводимых в Физико-техническом институте, которые "создали опору квантовой теории - экспериментальные основы теплового излучения". "Может быть,- прибавляет далее Зоммерфельд,- столь же велика заслуга института Нернста, который доставил нам в планомерных измерениях удельных теплоемкостей другую, не менее важную опору квантовой теории".

Факты показывают, что применение квантовой теории к проблеме теплоемкости действительно сыграло важную роль в укреплении этой теории. Именно с этого времени у физиков возникает представление об универсальности теории, об общем смысле квантовой постоянной Планка, и сам доклад Зоммерфельда - яркое свидетельство этого обстоятельства.

Зоммерфельд указывает в своем докладе на другие возможности применения квантовой теории. К таким он относит прежде всего явления, наблюдаемые при низких температурах: открытую Каммерлинг-Оннесом сверхпроводимость и найденные Перье при низких температурах отклонения магнитной восприимчивости парамагнетиков от закона Кюри-Вейсса. Другая группа явлений примыкает к квантовым законам фотоэффекта, найденным Эйнштейном. Сюда Зоммерфельд относит гипотезу Штарка (1904, 1908) о том, что фиолетовая граница полосатого спектра связана с ионизационным потенциалом соотношением I = hv. Эта гипотеза была экспериментально исследована Штейнбингом в 1909 г. Все эти явления связаны с идеей световых квантов, введенной Эйнштейном. Эта идея ограничена периодическими процессами. Однако, как полагает Зоммерфельд, идея кванта действия имеет универсальное значение и может быть применена и к непериодическим молекулярным процессам. Исходя из того обстоятельства, что квант действия имеет размерность энергия×время, Зоммерфельд усматривает его универсальное значение в том, что он регулирует самым общим образом временное течение процессов, связанных с обменом энергией. "В самом общем случае большие количества энергии будут поглощаться или отдаваться материей за короткое время, а малые количества - за большое время, так что произведение энергии на время, или (подлежаший дальнейшему определению) интеграл энергии, определяется величиной h".

Это поразительное утверждение, предвосхищающее будущее соотношение неопределенности Гейзенберга, Зоммерфельд пытается оправдать экспериментальными данными. Так он указывает, что катодные лучи больших энергий при торможении дают жесткий рентгеновский импульс, медленные же электроны дают мягкие лучи. Зоммерфельд, следуя идеям Д. Д. Томсона и Вихерта, считает мерой жесткости ширину рентгеновского импульса: чем жестче лучи, тем уже импульс, тем меньше, по Зоммерфельду, время торможения катодных лучей. Таким образом, утверждает Зоммерфельд, лучи больших энергий тормозятся за меньшее время, чем лучи меньших энергий. "Этот результат, полностью подтверждаемый опытом,- пишет Зоммерфельд,- является тем не менее в высшей степени странным. Он противоречит любой аналогии из области баллистических опытов и дает нам качественное указание на то, что в чисто молекулярных процессах существенное значение имеет величина, определяемая произведением воспринятой энергии на требуемое для ее поглощения время".

Это место является, по-видимому, первым в истории квантовой физики указанием на то, что атомные процессы ("молекулярные", по терминологии Зоммерфельда) подчиняются своим странным законам, не имеющим аналогии в макроскопической механике. При этом указывается, что для этих атомных процессов существенную роль играет произведение энергии на время.

Но это еще не формулировка принципа неопределенности, а скорее его предчувствие. Пример Зоммерфельда ничего общего с принципом неопределенности не имеет - это просто пример на применение уравнения Эйнштейна для фотоэффекта. Зоммерфельд еще не знает опытов Лауэ-Брэггов, и волновая природа рентгеновских лучей пока не доказана. Для Зоммерфельда найденное им соотношение является интегральным принципом, который он далее формулирует следующим образом: "При всяком молекулярном процессе молекула поглощает или отдает определенное универсальное количество действия, имеющее величину .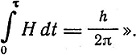

При этом τ определяет продолжительность действия, а величина Н есть функция Лагранжа Т-U. Таким образом, принцип Зоммерфельда - это принцип квантования, действия, сыгравший большую роль в старой атомной механике.

Зоммерфельд пытается применить свой принцип квантования действия к теории фотоэффекта. Как он указывает, его теория представляет собой нечто среднее между теорией Ленарда и теорией Эйнштейна. В теории Ленарда фотоэффект рассматривается как резонансный процесс, энергия которого заимствуется из атома. У Эйнштейна энергия электрона заимствуется из излучения. В теории Зоммерфельда энергия фотоэффекта, как и в теории Эйнштейна, заимствуется из излучения, но электрон освобождается из атома только по истечении некоторого "времени аккумуляции". Применив свой принцип к линейному незатухающему осциллятору, находящемуся под воздействием электрического поля световой волны, Зоммерфельд получает уравнение фотоэффекта Эйнштейна в случае резонанса, когда частота падающего излучения v совпадает с собственной частотой осциллятора v₀. В случае если v≠v₀, фотоэмиссия может происходить только если v>v₀. Поэтому график зависимости энергии фотоэлектрона Т от частоты падающего излучения v не выражается прямой линией, как у Эйнштейна, а имеет резонансные пики вблизи собственных частот. Таким образом, теория Зоммерфельда говорит об избирательном характере фотоэффекта, причем селективные частоты зависят от свойств освещаемого материала.

Однако эта полуклассическая теория фотоэффекта все же не рассматривается Зоммерфельдом как путь к классическому истолкованию кванта действия. Наоборот, Зоммерфельд считает, что не атомные (молекулярные) размеры определяют, но "само существование молекул рассматривается как функция и следствие элементарного кванта действия. Какое-либо электромагнитное или механическое "объяснение" мне кажется столь же мало уместным и перспективным, как и механическое "объяснение" уравнений Максвелла" (курсив мой.- П. К.). "Было бы много полезнее,- продолжает Зоммерфельд,- проследить гипотезу во всех ее многочисленных следствиях и свести к ней другие явления. Если наша физика нуждается, в чем едва ли можно сомневаться, в новых фундаментальных гипотезах, которые добавлялись бы как нечто непривычное к электромагнитной картине мира, то, как мне кажется, к этому более других призвана гипотеза кванта действия".

Именно в этих тонких и проницательных замечаниях по поводу гипотезы кванта действия и заключается важное историческое значение доклада Зоммерфельда. Он понял принципиальное значение гипотезы квантов, ее фундаментальный характер, не сводимый к классическим понятиям. Правда, Зоммерфельд чувствует неясность и темноту квантовых представлений, но это не смущает его. "Но научный оптимизм,- говорит он,- который является основным обязательным принципом прогресса, заставляет нас верить в то, что эта темнота в недалеком будущем рассеется и физические принципы предстанут тогда перед нашим взором во всем ярком свете".

Оптимизм ученого восторжествовал, как и восторжествовало его убеждение в невозможности "объяснения" кванта классически.

Но в 1911 г. положение оставалось далеко не ясным. Разногласия во взглядах на квантовые явления достигли большой остроты. Начиная с 1910 г. ведущие ученые глубоко сознавали, что необходимо обсудить коллективно назревшие трудные вопросы. Так Планк в письме к Нернсту от 11 июня 1910 г. писал: "В области законов излучения, удельной теплоемкости и т. д. создавшееся ныне состояние теории, исполненное пробелов, стало невыносимым для каждого настоящего теоретика". Планк добавлял: "Отсюда вытекает необходимость объединиться и совместно продумать, как помочь делу".

Как раз в эти годы известный изобретатель аммиачного способа производства соды, бельгийский капиталист Эрнст Сольвей выделил средства на организацию Сольвеевских конгрессов по животрепещущим проблемам физики. "Он воспринял с энтузиазмом,- писал о Сольвее Лоренц,- высказанную проф. Нернстом в Берлине идею и собрал осенью 1911 г. небольшой кружок физиков из различных стран, чтобы в многодневных заседаниях обсудить важнейшие проблемы современного естествознания".

По окончании конгресса Сольвей в целях материальной поддержки научных исследований по физике учредил Международный институт физики, в распоряжение которого выделил миллион франков. Во главе института стал комитет под председательством Лоренца. В число членов комитета вошли: от Франции - Мария Кюри-Склодовская и М. Бриллюэн, от Германии - Э. Варбург и В. Нернст, от Голландии, кроме Лоренца,- Каммерлинг-Оннес, от Англии - Э. Резерфорд, от Дании - М. Кнудсен.

В первом Сольвеевском конгрессе, посвященном теме "Излучение и кванты" и проходившем с 3 октября по 3 ноября 1911 г., приняли участие: от Франции - Марсель Бриллюэн, Поль Ланжевен, Жан Перрен и Анри Пуанкаре, от Германии - Макс Планк, Вальтер Нернст, Генрих Рубенс, Арнольд Зоммерфельд, Вильгельм Вин, Эмиль Варбург, от Англии - Эрнст Резерфорд и Джемс Джинс, от Австрии - Альберт Эйнштейн и Фриц Газенорль,. от Голландии - Хейке Каммерлинг-Оннес и Гендрик Лоренц, от Дании - М. Кнудсен. На конгрессе состоялись доклады Лоренца, Джинса, Варбурга, Рубенса, Планка, Кнуд-сена, Перрена, Нернста, Каммерлинг-Оннеса, Зоммерфельда, Ланжевена, Эйнштейна. Проблема излучения и гипотезы квантов трактовалась в докладах Лоренца, Варбурга, Рубенса, Планка. Проблему теплоемкости и теории квантов в физико-химических проблемах рассматривали Джинс, Нернст, Эйнштейн, Кнудсен. Каммерлинг-Оннес делал доклад о сверхпроводимости, Ланжевен - о теории магнетизма. Как мы уже говорили, Лоренц в своем докладе "О применении к излучению теории равномерного распределения энергии по степеням свободы" показал, что теорема равномерного распределения энергии по степеням свободы, примененная к излучению, с необходимостью ведет к закону Рэлея-Джинса.

Участники Сольвеевского конгресса 1921 г. В первом ряду: А. Майкельсон, П. Вейсс, М. Бриллюэн, Э. Соль вей, Г. А. Лоренц, Э. Резерфорд, Р. Милликен, М. Кюри. Во втором ряду: М. Кнудсен, Ж. Перрен, П. Ланжевен, О. Ричардсон, Д. Лармор, X. Кармерлинг-Оннес, П. Зееман, М. де Бройль. В третьем ряду: У. Л. Брэгг, 3. фон Аубель, В. де Гааз, Э. Герцен, Э. Баркла, П. Эренфест, М. Зигбан, И. Фершафельт, Л. Бриллюэн

Планк в своем докладе излагал свой новый вариант теории, приводящий к наименьшему значению энергии ^hv/₂. Мы уже приводили изложение этого варианта его теории, и здесь ограничимся только краткой характеристикой его словами самого Планка.

"Я сам пришел к результату, что" энергия определенного периодического колебания может принимать любое произвольное значение от 0 до ∞, но что она меняется непрерывно только при возрастании, наоборот, при убывании делает скачки, а именно уменьшается всегда только от целого кратного hv до нуля".

При этом выражение тепловой энергии тела имеет вид

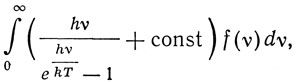
и константа в этом выражении будет равна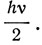

Другая часть доклада Планка была посвящена новой формулировке квантовой гипотезы. Пуанкаре цитирует основные положения этой формулировки из доклада: "Вероятность непрерывной переменной получится, если мы будем рассматривать элементарные независимые области равной вероятности... Для того чтобы найти эти элементарные области, в классической динамике пользуются теоремой, гласящей, что два физических состояния, из которых одно является необходимым результатом другого, одинаково вероятные. В физической системе если мы выразим через q одну из обобщенных координат, через р - соответствующий момент, то согласно теореме Лиувилля область ∫ pdq, рассматриваемая в какой-нибудь момент, будет неизменной величиной по отношению ко времени, если q и р изменяются соответственно уравнениям Гамильтона. С другой стороны, q и р могут в данный момент принимать всевозможные значения независимо друг от друга. Отсюда следует, что элементарная область вероятности неизмеримо мала, имея порядок величины dpdq. Новая гипотеза должна иметь целью ограничение изменяемости q и р, так чтобы эти переменные изменялись уже только скачками или чтобы они рассматривались как частью связанные одна с другой. Мы приходим, таким образом, к уменьшению количества элементарных областей, так что пространство, занимаемое каждой из них, увеличивается. Гипотеза квантов действия заключается в предположении, что эти области, будучи равными между собой, уже не бесконечно малы, но конечны и что для каждой из них мы имеем формулу

где h - постоянная величина".

Плоскость переменных (обобщенных координат) и соответствующих импульсов (моментов) называется фазовой плоскостью. Периодический процесс изображается на этой плоскости замкнутой фазовой кривой. Новое правило квантования Планка состоит в том, что площадь, заключающаяся между двумя последовательными допустимыми с точки зрения теории квантов кривыми, должна равняться кванту действия h. Допустимыми же с точки зрения теории квантов фазовыми кривыми являются кривые, ограничивающие площадь, кратную кванту действия:

Так, для гармонического осциллятора q = x = a sin ωt, p = mx = mωa cos ωt. Уравнение фазовой кривой есть уравнение эллипса

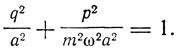
Площадь эллипса S = πab = πa²mω = nh.

Но энергия осциллятора

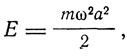
Отсюда E = nhv, т. е. гипотеза квантов энергии. Эта новая формулировка квантовой гипотезы очень близко примыкает к идеям Зоммерфельда, который, как мы видели, принимал действие ∫ Ldt равным ^h/_2π. Планк назвал теорию Зоммерфельда "смелой и очень интересной". Эту теорию отмечал и Пуанкаре, считая, что она объясняет "почему Х-лучи бывают тем проницательнее и тем "жестче", чем больше скорость катодных лучей".

Впрочем, и значительно позже, в 1918 г. Ф. Рейхе, излагая теорию Зоммерфельда, писал, что Зоммерфельд "с успехом применил свою теорию к объяснению механизма возбуждения рентгеновских лучей и γ-лучей". В то время физики не могли еще дать правильную оценку возникающим теориям. Их ошеломило само вторжение прерывности в мир физических законов. "Мы уже не ограничиваемся вопросом, должны ли быть изменены дифференциальные уравнения динамики,- писал Пуанкаре, сравнивая переворот, вызванный теорией относительности, с переворотом, вызванным теорией квантов,- мы уже спрашиваем себя, могут еще законы быть выражены с помощью дифференциальных уравнений".

"И в этом-то,- продолжает Пуанкаре,- и состоит наиболее глубокая революция, какую только переживала философия природы со времен Ньютона".

Но революция еще только начиналась. Еще можно было думать, что классическая электродинамика может быть спасена (в этом и заключалась цель второй теории Планка). Говоря о Сольвеевском конгрессе, русский физик Н. А. Умов писал: "Здесь обнаружилось, что теории излучения основываются частью на старых, частью на новых учениях, что они не представляют цельности в своих методах и не могут быть рассматриваемы как окончательные".

Эта борьба старого и нового характерна для всего периода, вплоть до создания новой квантовой механики, которая наконец-то привела к столь страстно желаемой законченности и цельности. Но эта законченность и цельность были достигнуты путем отказа от классических, привычных представлений.

Вскоре после конгресса 16 декабря 1911 г. Планк выступил с докладом "О новых термодинамических теориях" в Немецком химическом обществе в Берлине. Здесь Планк связывает тепловую теорему Нернста с гипотезой квантов. Планк, по-видимому, был первым из физиков, кто понял, что "вычисление кривых упругости паров и химических равновесий становится в зависимость от планковской постоянной h". Разбирая основные принципы термодинамики и останавливаясь на основных термодинамических функциях: внутренней энергии, энтропии, свободной энергии и термодинамическом потенциале, Планк указывает, что в определениях всех этих функций содержатся неопределенные постоянные, которые классическая термодинамика не в состоянии определить. "Таково было состояние теории,- пишет Планк,- когда шесть лет тому назад В. Нернст выступил с изумительной гипотезой, значение которой, коротко говоря, заключается в том, что она чрезвычайно простым способом и в то же время применимо ко всем вообще случаям устанавливает значение аддитивной константы в выражении энтропии S, которое классическая термодинамика оставляла еще неопределенным".

Планк дает свою формулировку теоремы Нернста, которая как он пишет, "по моему мнению, является наиболее глубокой и в то же время самой простой". Вот эта формулировка Планка: "Энтропия конденсированного (т. е. твердого или жидкого) химически гомогенного вещества при нуле абсолютной температуры равна нулю". Из этой формулировки вытекает в качестве следствия и вывод сформулированный Нернстом в качестве теплового закона, что теплоемкость всех конденсированных химически однородных веществ при приближении к абсолютному нулю стремится к нулю.

Для химически однородного идеального газа классическая термодинамика дает выражение энтропии:

где n - число молекул, р - давление, С_р - молекулярная теплоемкость при постоянном давлении, R - газовая постоянная, k - неопределенная константа. "Нернстова теорема теплоты,- указывает Планк,- делает это выражение более точным в том отношении, что константа имеет вполне определенное, измеримое значение, характерное для всех физико-химических свойств газа. Поэтому указанную константу можно назвать химической константой газа".

Это важное значение химической постоянной газа стимулировало поиски ее теоретического расчета. Замечательные результаты получил в 1911-1913 гг. О. Саккур, который показал, что эта постоянная может быть вычислена для одноатомных газов из числа п, массы молекул и универсальных постоянных Больц-мана и Планка. Об этих результатах Саккура, полученных также Г. Тетроде (1912) и О. Штерном (1913), мы скажем дальше, а пока продолжим изложение доклада Планка. Указав на большое принципиальное значение теоремы Нернста и пояснив это значение на ряде примеров, Планк подходит к выяснению глубокого физического смысла этой теоремы. Этот смысл раскрывается в атомистике. Планк обращается к знаменитому соотношению Больцмана между энтропией и термодинамической вероятностью, которое, по его мнению, позволит уяснить атомистическое значение константы энтропии и, следовательно, теоремы Нернста. Для вычисления термодинамической вероятности состояния надо подсчитать распределение молекул по интервалам энергии. Величины этого интервала в классической статистике оставались произвольными лишь бы они были физически бесконечно малыми. Эта неопределенность в определении величин интервала и приводила к неопределенности в выражении энтропии.

"Аддитивная константа в выражении энтропии,- пишет Планк,- оставляемая неопределенной классической термодинамикой, соответствует с атомистической точки зрения неопределенности элементарных областей вероятности, которыми мы пользуемся для вычисления энтропии; а так как тепловая теорема Нернста определенно устанавливает значение этой константы, то физическое содержание этой теоремы, будучи выражено в самой общей форме, состоит в том, что элементарные области вероятности не могут быть как угодно малы, но имеют вполне определенную величину, которую во многих случаях можно прямо указать".

В этом утверждении содержится исходный пункт квантовой статистики. Не мудрено, что он казался "всякому, кто занимается более близким изучением молекулярных процессов, странным и в высшей степени поразительным". Планк указывает, однако, что к этой гипотезе вынуждают поразительные результаты, достигнутые в теории излучения и теории теплоемкости. "Ввиду таких результатов представляется едва ли допустимым долее говорить здесь о случайности". Но именно это обстоятельство делает особенно актуальной проблему: "Найти самую сущность и более глубокое физическое значение гипотезы, согласно которой для термодинамической вероятности существуют вполне определенные элементарные области, потому что,- добавляет Планк,- именно так мне хотелось бы формулировать истинное содержание так называемой гипотезы квантов".

Планк указывает, что Саккур недавно произвел вычисление таких элементарных областей. Он имеет в виду работу Саккура 1911 г., в которой последний производил расчет химической постоянной, исходя из гипотезы квантов. Но само обоснование гипотезы Планку кажется в высшей степени трудным. Предположение, что сама энергия квантуется, Планк решительно отвергает: "Мы не можем считать мыслимым прерывистое, скачкообразное изменение кинетической энергии прямолинейно-поступательного движения". Правда, гипотеза квантов энергии колебательного движения выдвигалась и защищалась. "Последнего предположения,- пишет Планк о квантах энергии колебательного движения,- я и сам раньше придерживался, но теперь отказался от него, так как и его считаю слишком радикальным для того, чтобы исходить из него во всех случаях".

"Однако,- продолжает Планк,- нет никакой надобности идти так далеко. Гипотеза квантов требует только, чтобы в элементарных законах, которым подчинены атомистические силы, заключалась некоторая прерывистость, скачкообразность, результатом которой были бы отдельные рассеянные в пространстве и не связанные непрерывно (дискретные) области вероятности. О природе такой прерывистости ничего нельзя сказать наперед, и надо принять во внимание, что строение из элементарных количеств относится ближайшим образом не к энергии, а к вероятности" (курсив мой.- П. К.).

Далее Планк указывает, что о квантах энергии можно говорить только в периодических процессах. "Для непериодических процессов А. Зоммерфельд недавно предложил в общих чертах очень смелую и очень интересную теорию, в которой, разумеется, играют роль только элементарные количества действия, а не энергии".

Несмотря на такие разногласия в гипотезе квантов, Планк убежден, что "этой гипотезой заложен фундамент для сооружения здания теории, которой предназначено в будущем пролить новый свет на детали тонких и быстрых процессов, происходящих в молекулярном мире".

Эти замечательные идеи Планка расширяли область применения гипотезы квантов и начинали развитие квантовой статистики. Теорию одноатомных газов с точки зрения теории квантов разрабатывали также Саккур и Тетроде. Результаты этих исследований сыграли важную роль в развитии статистики и поныне входят во все учебники термодинамики и статистической физики. Для давления одноатомных газов термодинамика дает выражение

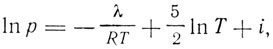
здесь λ - скрытая теплота парообразования, R - газовая постоянная, Т - абсолютная температура, i - некоторая постоянная, которую классическая термодинамика оставляет неопределенной. Эта постоянная тесно связана с постоянной в выражении энтропии, будучи ей пропорциональной. Нернст назвал ее химической постоянной и указал, что она "зависит только от природы взятого газа и не зависит от свойств рассматриваемого физического или химического равновесного состояния". Это свойство химической постоянной вытекало из его теплового закона и приводило к выводу о возможности вычисления ее путем простого теоретического расчета. "Различные исследователи,- писал Нернст,- побуждаемые этим предположением, занялись разработкой этого вопроса и получили чрезвычайно важное и замечательное соотношение:

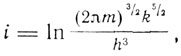
где m = ^M/_N есть масса атома, k = ^К/_N (N - число молекул в одном моле), h - планковская постоянная". Это выражение было получено почти одновременно О. Саккуром и Г. Тетроде в 1912 г. и получило название формулы Саккура-Тетроде. Нередко формулой Саккура-Тетроде называют формулу для энтропии одного моля:

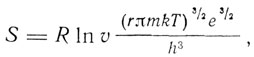
где e - основание натуральных логарифмов. В этом случае константа энтропии для одного моля будет

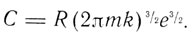
В 1913 г. теоретический вывод формулы Саккура-Тетроде дал О. Штерн, впоследствии получивший Нобелевскую премию за открытый им метод молекулярных пучков. Основную идею расчета Штерна Нернст излагает следующим образом: "Наш тепловой закон устанавливает, что i не зависит ни от природы конденсата, ни даже от природы рассматриваемого равновесного процесса. Поэтому если бы удалось создать возможно простую модель твердого тела, находящегося в равновесии со своими насыщенными парами, для которой мы могли бы произвести расчет, то с очень большой вероятностью можно было бы считать полученное таким путем для i значение пригодным и для всех других случаев, как бы сложны они ни были".

Такой моделью у Штерна была совокупность атомов - осцилляторов, подчиняющихся эйнштейновскому закону твердого тела, каждый из которых колебался внутри ограниченной сферы действия, вне которой его можно считать свободным. Расчет Штерна изложен как у Нернста, так и в современном курсе термодинамики Эпштейна.

Обращаясь к выводу Саккура, следует отметить, что, основываясь на теории квантов и вероятностной интерпретации энтропии, он уже в 1911 г. показал связь теоремы Нернста с квантовыми представлениями, как это было сделано и Планком в рассмотренном нами выше докладе.

В 1912 г. Саккур и независимо от него Тетроде пришли к выводу, что фазовый объем одноатомного газа равен h³. В 1913 г. в Геттингенском университете состоялась серия докладов по кинетической теории материи и электричества. Доклады делали М. Планк, П. Дебай, М. Смолуховский, Г. Лоренц и А. Зоммерфельд, X. Каммерлинг-Оннес и В. Кеезом. Доклад "Современное значение квантовой гипотезы для кинетической теории газов" сделал М. Планк. Он вновь подчеркнул, что квантовая гипотеза требует определенной конечной величины ячеек фазового пространства, в отличие от статистики Больцмана оставлявшей их неопределенными. Тем самым получает определенное значение постоянная энтропии и Планк выписывает значение энтропии, полученное на основе квантовой гипотезы:

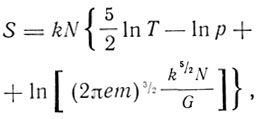
где e - основание натуральных логарифмов, G - величина фазового объема,

где ξ, η, ζ - компоненты импульса. "Чтобы эта величина,- пишет Планк,- как этого требует квантовая гипотеза, имела определенное значение, пределы интеграла, естественно, должны быть вполне определенными, и фундаментальной важности задача теории состоит в том, чтобы выяснить физическое значение этих пределов". Планк указывает, прежде всего, что эта область G пропорциональна числу атомов: G = Ng, где g уже не зависит от числа атомов. Далее он получает формулу Нернста для давления насыщенного пара:

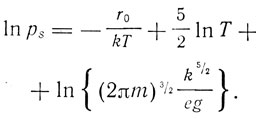
В этом уравнении ясно видна связь химической постоянной Нернста с элементарной ячейкой фазового объема g, имеющей размерность энергия×время.

"О. Саккур и Г. Тетроде,- пишет Планк,- исходя из выполненных до сих пор измерений, именно с аргоном и ртутью, пришли к заключению, что g = h³, где h означает выведенный из теплового излучения универсальный квант действия около 6,4*10^-27 эрг*сек. Если это следствие оправдается, если при этом окажется, что только g является величиной, не зависящей от природы газа и отличающейся от h³ только числовым множителем, то тем самым будет получен результат такого фундаментального значения для всей термодинамики и всего учения о химическом сродстве, что я хочу здесь обратиться с призывом ко всем тем, кто в состоянии выполнять такого рода измерения, чтобы этот принципиальный вопрос был решен возможно скорее и возможно основательнее. Их решение в ту или другую сторону будет, в свою очередь, содействовать тем, кто поставил целью дальнейшее развитие квантовой гипотезы в области кинетической теории материи".

Планк ясно видел глубокое значение гипотезы Саккура и Тетроде, которая ныне стала основным принципом квантовой статистики. Найденное ими значение химической постоянной, кроме того, подводило к вопросу о справедливости газовых законов вблизи абсолютного нуля. Уже в это время начала выкристаллизовываться идея вырождения газа. Тетроде (1913), Зоммерфельд (1913) и Кеезом (1914) выдвинули гипотезу, что при низких температурах газ становится подобным твердому телу, что и для газов энтропия при абсолютном нуле обращается в нуль. Нернст (1916) представлял, что "при низких температурах поступательное движение газовых молекул под влиянием происходящего в нулевой точке излучения эфира все более переходит во вращательное движение, таким образом, что в самой точке абсолютного нуля газовые молекулы уже вращаются с постоянной скоростью вокруг равномерно распределенных в пространстве точек равновесия".

Явление вырождения газов было полностью объяснено квантовой статистикой.

Саккуру принадлежит также важная идея, относящаяся к общей концепции кванта действия. Мы говорили уже о найденном Зоммерфельдом соотношении между энергией и временем ее действия, связанном с понятием кванта действия. Принцип Зоммерфельда произвел большое впечатление на современников, и мы уже приводили ряд высказываний, относящихся к этому принципу. Приведем еще высказывание русского физика Николая Алексеевича Умова о принципе Зоммерфельда, взятое из его доклада "Эволюция физических наук и ее идейное значение", прочитанного 29 декабря 1913 г. на съезде преподавателей физики, химии и космографии.

"По мнению Зоммерфельда,- говорит Н. А. Умов,- теория квантов указывает на существование общего закона, регулирующего течение молекулярных процессов. Время, потребное материи, чтобы заимствовать или отдать некоторое количество энергии, тем короче, чем эта энергия больше. Обмен большими количествами энергии происходит в короткое время, а малыми - в продолжительное, так что произведение количества энергии на время обмена есть кратное от кванта, которое является не элементом энергии, а элементом действия, представляемым произведением энергии на время. Все молекулярные процессы сопровождаются обменом энергиями; поэтому, по Зоммерфельду, течение молекулярных процессов совершается определенными порциями действия. Его закон гласит: во всяком элементарном молекулярном явлении действие, поглощенное или потерянное молекулой, имеет вполне определенную универсальную величину ^h/_2π. Этот закон находит свое оправдание в тех процессах, в которых смысл термина - молекулярное явление - и продолжительность последнего могут быть точно установлены".

Вот этот-то принцип Зоммерфельда и привлек внимание Сак-кура.

25 октября 1912 г. он сделал на заседании Немецкого физического общества доклад "Универсальное значение так называемого элементарного кванта действия".

Саккур начинает свой доклад с упоминания о работах по вычислению постоянной энтропии и химической постоянной. "В двух недавно появившихся работах,- пишет он, имея в виду свои статьи 1911 и 1912 гг.,- я пытался показать, что константа энтропии и вместе с тем введенная Нернстом "химическая постоянная", определяющая химическое поведение газа и давление пара его конденсата, определяются так называемой элементарной областью dσ".

Эта элементарная область dσ, о которой говорит Саккур, есть та область фазового пространства, о которой писал Планк, называя ее элементарной областью вероятности. Она, как пишет Саккур, "может быть вычислена для однратомных газов из числа молекул и их массы и универсальных постоянных... Я пришел к этому результату с помощью гипотезы Зоммерфельда, что каждое действие является целократным элементарного действия h. Но так как действие определяется произведением энергии на время, т. е. произведением двух величин, принимаемых до сих пор всеми за непрерывные, то эта гипотеза кажется в высшей степени странной". Саккур и ставит своей задачей объяснение постоянной Планка "менее странным образом", не отказываясь от непрерывности энергии. С этой целью он рассматривает, как и в теории излучения, систему из N осцилляторов с заданной полной энергией Е. Как и в теории твердого тела Эйнштейна, он считает период колебаний τ всех осцилляторов одинаковым, а сами осцилляторы - взаимодействующими друг с другом только посредством излучения. Состояние каждого осциллятора определяется его энергией ε. Саккур задает вопрос: какова вероятность того, что атом, проходя через положение равновесия, обладает энергией ε? Он указывает, что эта вероятность будет конечной только тогда, "когда мы будем рассматривать энергию равной не в точности ε, а заключающейся между ей ε+dε". Вместе с тем и время прохождения атома через положение равновесия не должно быть бесконечно малым, а иметь некоторое конечное значение Δt. "Только для конечного времени наблюдения и конечного интеграла энергии мы получим конечную вероятность, причем она будет тем больше, чем большими мы выберем интервал энергии Δε и время наблюдения Δt". Это очень интересная постановка вопроса, совершенно в духе современной квантовой механики, где неопределенность в измерении наблюдаемых сопряженных величин является совершенно обязательной. Саккур полагает, что в простейшем случае искомая вероятность обнаружить атом в интервале энергии Де за время наблюдения At пропорциональна произведению этих интервалов:

При этом вероятность определяется отношением числа атомов п, соответствующих данным условиям, к полному числу атомов (осцилляторов) N:ω = ⁿ/_N, и поэтому

Далее Саккур описывает мысленный эксперимент, позволяющий определить n. Наблюдатель, обладающий способностью видеть и считать атомы (нечто вроде максвелловского демона), дает сигнал всякий раз, когда атом с энергией в пределах от ε до ε+dε проходит через положение равновесия. Тогда n равно числу сигналов, посылаемых наблюдателем за время Δt. Если число n постоянно, т. е. вероятность обнаружить атом в этом состоянии постоянна, то произведение Δε*Δt должно быть постоянным. "Это столь естественное допущение сначала является произвольным, однако оно будет подтверждено согласием его следствий с опытом". Поэтому для одинаковых вероятностей ω произведение Δε*Δt должно быть постоянной и именно универсальной постоянной. Все же величины, характерные для данной системы (объем v, энергия E, масса атомов m и т. д.), должны входить в функцию f.

Обозначим

и, следовательно,

Равенство Δε*Δt = h, по Саккуру, является, следовательно, определением h. Из него следует, что для бесконечного времени наблюдения (Δt = ∞) имеется конечная вероятность того, что атом будет обладать энергией, в точности равной ε (Δε = 0). Для того чтобы сумма ∑n = ∑ Nhf(ε) равнялась N, а не была бесконечной, необходимо, чтобы атом считался только один раз. Таким образом, время наблюдения Δt должно быть таким, чтобы за это время атом проходил через положение равновесия только один раз. Но для этого, очевидно, время наблюдения должно равняться периоду колебаний τ. Тогда

т. е. энергия осциллятора квантуется.

Таковы принципиальные соображения Саккура. Важность их не подлежит сомнению. Саккур пошел дальше Зоммерфельда, который выразил свой принцип в интегральной форме. Саккур же придал ему форму, тождественную с современной формой соотношения неопределенностей. Это соотношение у Саккура является определением постоянной Планка. Сам Саккур хорошо сознавал новый и принципиальный характер своего определения. Когда вскоре после публикации доклада Саккура К. Эйзенман заявил претензию на приоритет вывода эйнштейновской формулы энергии твердого тела, содержащейся в статье Саккура, то Саккур решительно возразил, что суть его работы не в этом выводе. "Данное мною определение постоянной n,- писал Саккур в своем ответе Эйзенману,- и вытекающий отсюда вывод уравнения излучения, поскольку он выходит за рамки рассуждений Планка и Эйнштейна (курсив мой.- П. К.), в статье Эйзенмана не содержится".

Опираясь на свое определение h, Саккур получил и закон излучения Планка, и уравнение Эйнштейна для теплоемкости. Вместе с тем он дал новый вывод выражения энтропии идеального газа. Это выражение имеет вид

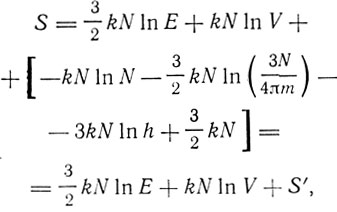
где

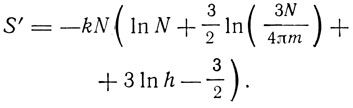
"Это уравнение,- пишет Саккур,- полностью совпадает с ранее выведенным уравнением энтропии для идеального газа, если мы положим там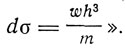

Далее он приводит данные эмпирической проверки его уравнений по кривой давления ртутных паров. "Согласие вычисленной и экспериментально определенной кривой давления вполне хорошее... Тем самым впервые проведен расчет кривой давления пара из определяемых калориметрических величин; одновременно получается новое непосредственное подтверждение теоремы Нернста, которая предполагалась при выводе уравнения давления пара".

Таковы замечательные результаты Саккура. Однако если его формула химической постоянной и постоянной энергии не была забыта, то его определение постоянной Планка постигла другая участь. Его не вспомнили даже тогда, когда уравнение ΔE*Δt = h и эквивалентное ему соотношение Δp*Δq = h вошли во все учебники.

В этом, по-видимому, виноват сам Саккур, который не только не мог понять истинного смысла своего соотношения, но и неправильно думал, что оно избавляет от квантования энергии. Он думал, что данный вывод энергии и энтропии идеального газа не нуждается "в противоположность старому, обоснованному Планком представлению" в том, чтобы "приписывать энергии или действию атомную структуру".

Само представление h в виде двух множителей Δε и Δt Саккур считал только "вычислительным приемом", который необходим для расчета констант, входящих в выражение энтропии. Он полагал, что взамен "странного "принципа квантования" непрерывной" энергии им дано физическое понятие вероятности, основанное на "почти само собой разумеющемся допущении, что наступление событий будет тем более вероятным, чем больше предоставляется времени на его появление".

Как бы то ни было, самый факт написания в 1912 г. соотношения неопределенности

является замечательным и не может быть обойден историком квантовой физики.

Н. А. Умов

Вскоре после Саккура принципиальная сторона концепции квантов подверглась обсуждению в статье русского физика Н. А. Умова "Возможный смысл теории квантов", опубликованной в 1913 г. Эта статья в ее выводах удивительным образом перекликается со статьей Саккура. При этом если Саккур ставил своей целью сделать менее странным принцип Зоммерфельда, то Умов пытался спасти закон равномерного распределения энергии по степеням свободы. С этой целью он рассматривает состояние системы по отношению к окружающему агенту - эфиру - и задается вопросом о том, какие движения по отношению к этому агенту являются упорядоченными и какие неупорядоченными. Чувствительность агента - эфира - по отношению к движениям моделируется некоторым манометром. Если манометр, подобный обычному манометру, воспринимает только действие всей совокупности молекул, то для такого манометра сумма энергий неупорядоченных движений равнялась нулю. Манометр типа демона Максвелла способен воспринимать импульсы отдельных молекул, и для него вся энергия будет энергией неупорядоченных движений. "Между этими крайними типами могут быть вставлены манометры, чувствительность которых определяется способностью воспринимать группы импульсов, энергия которых лежит между пределами: произвольным Е и другим Е + ε, где величину ε мы будем считать пока определяемой природой манометра и дробь ¹/_ε - мерой его чувствительности. Для обыкновенного манометра ε = ∞ и чувствительность равна 0; для демона Максвелла ε = 0 и чувствительность бесконечно велика",- пишет Умов в своей работе.

Очень интересно наблюдать, как самыми различными путями входит идея неопределенности измерения. Саккур представляет наблюдателя, который регистрирует атомы с энергией Е с неопределенностью ΔЕ. Умов воображает некий прибор - манометр, выполняющий ту же функцию с определенной чувствительностью. Обрабатывая математически свою идею, Умов получает формулу Планка. Его окончательный вывод формулируется следующим образом: "Эфир обладает различной степенью чувствительности по отношению к неупорядоченным движениям материальных систем. Эта чувствительность зависит от числа естественных колебаний молекулы и представляется величиной ¹/_hv, где h есть постоянная, зависящая от свойств эфира и потому универсальная, a v есть число естественных колебаний молекулы системы". Таким образом, если обозначить наименьшую энергию, воспринимаемую прибором - эфиром,- через ΔE, а период молекулы ¹/_v через Δt, то вывод Умова представляется формулой Саккура

Комментируя этот вывод Умова, проф. А. С. Предводителев, впервые обративший внимание на то, что он совпадает с принципом неопределенности, писал: "Таким образом, мы видим, насколько близко Умов подходил уже тогда к современным воззрениям волновой механики. По сути дела, он первый в истории развития теории квантов осмелился сказать о приближенном характере измерений параметров, определяющих состояние системы".

Мы закончим эту главу рассмотрением теории "световых атомов" М. Вольфке, изложенной им же в двух сообщениях в октябре-ноябре 1911 г. Вольфке исходит из гипотезы Эйнштейна, что "световая энергия не только при испускании и, возможно, при поглощении, но и в свободном пространстве обладает прерывным характером". Исходя из этого, Вольфке предполагает, что "световая энергия распространяется в пространстве не непрерывно, а локализована в очень большом конечном числе центров". Эти центры Вольфке называет атомами света. Он принимает, что эти атомы не могут сами по себе возникать и исчезать, они порождаются и поглощаются материальными телами. Он полагает далее, что число световых атомов в вакууме не может быть изменено отражением от абсолютно отражающих поверхностей. И наконец, в соответствии с фактом существования светового давления он принимает, что световые атомы оказывают на поглощающую или отражающую поверхность давление, пропорциональное переносимой ими энергии. Далее, опираясь на теорию отражения света от движущегося зеркала, он формулирует основной закон световых атомов: "Световой атом может изменять энергию и частоту только одновременно и притом так, что отношение энергии и частоты остается постоянным ^ε/_v = α". Вольфке использует концепцию световых атомов для вывода закона Планка, исходя из статистических соображений и закона Вина. Он получает формулу для плотности энергии излучения в виде

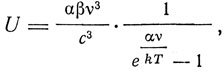
из которой следует, что а тождественно с планковской постоянной h. Он находит, что ^α/_k = 4,79*10^-11, βk = 3,37*10^-5, и, полагая k = 1,34*10^-16, находит α = 6,42*10^-27. Он вычисляет также массу светового атома

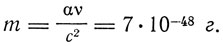
Так развивалась концепция квантов. Но в том же, 1913 г. произошло важнейшее событие, круто повернувшее развитие теории квантов: Н. Бор применил гипотезу квантов к теории строения атома. Этот шаг был подготовлен не только развитием квантовой теории, но и экспериментальными исследованиями взаимодействия излучения с веществом. К этим исследованиям мы и обращаемся.