
Глава десятая. Спектры и теория атома Бора
Спектральные серии
"Лет пятнадцать тому назад в отношении проблемы излучения физика находилась в очень странном состоянии. Были четыре отдельные главы физики, сами по себе хорошо обоснованные, но связи между ними не существовало; они были даже до некоторой степени несовместимы одна с другой. Первая глава - это классическая электродинамика, завершенная блестящей электронной теорией Лоренца и Лармора. Вторая глава - данные опыта о спектрах, объединенные эмпирическими законами Бальмера, Ритца и Ридберга. Третья глава - данные Резерфорда о нуклеарном атоме и, наконец, четвертая - квантовая теория черного излучения Планка. Ясно было, что развитие теории излучения и строения атома застынет до тех пор, пока эти четыре области остаются разрозненными и одна с другой не связанными". Так писали в начале 20-х годов нашего века сотрудники Бора Г. А. Крамерс и X. Гольет. Характеристика ситуации, сложившейся в физике перед открытием Бора, указана ими абсолютно точно. Нами были уже рассмотрены принципы электрической теории материи Лоренца и Лармора, мы рассмотрели также работы Резерфорда, приведшие к возникновению ядерной модели атома, и подробно осветили развитие квантовой теории Планка. Теперь нам осталось рассмотреть вопрос о спектрах и основные предпосылки теории атома Бора будут нами исчерпаны.
Уже со времен открытия Кирхгофом и Бунзеном спектрального анализа стало ясно, что каждому химическому элементу, излучающему в газообразном состоянии, соответствует свой определенный набор спектральных линий. Классическим примером, с которого, собственно, и началось открытие Кирхгофа, является желтая линия натрия, точнее дублет линий. Этот факт, как мы уже видели во втором томе этой книги, дал возможность открытия новых элементов по испускаемому ими спектру. Вполне естественно, что линейчатые спектры стали тщательно исследоваться и описываться. Исследование показало, что в линейчатом спектре линии группируются в отдельные серии. Такова главная серия с наиболее интенсивными линиями, диффузная, или первая побочная серия с размытыми линиями, резкая, или вторая побочная серия и т. д. Выделить из линий спектра серии нелегко; линии, принадлежащие одной и той же серии, нередко перепутаны между собой. Индентификация серии основана на одинаковых физических свойствах линий одной и той же серии, например все линии диффузной серии размыты. В каждой серии наблюдается уменьшение интенсивности линий по мере приближения к концу серии, конец серии характеризуется все большим и большим сгущением линий, сходящихся к общему пределу. Линии одной и той же серии одинаковой структуры, либо все сингулеты (единичные линии), либо все дублеты (двойные линии), либо все триплеты (тройные линии). Линии одной и той же серии одинаково расщепляются в магнитном поле (эффект Зеемана).
Одной из первых изученных серий была серия в видимой части водородного спектра. Здесь были описаны и измерены четыре линии в видимой части спектра: линия Нα (6563 А0), Нβ (4861 A0), Hγ (4340 А0) и Нδ (4102 А0). В 1885 г. швейцарский учитель И. Бальмер нашел эмпирическую формулу, позволяющую с большой точностью вычислить длины волн всех линий водородной серии. Эта формула имела вид
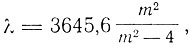
m = 3, 4, 5, 6.
Во время солнечного затмения 1899 г. было найдено более двадцати линий в ультрафиолетовой части и позднее было показано, что все двадцать девять линий хорошо укладываются в формулу Бальмера.
К этому времени Г. Кайзер и К. Рунге в серии работ в 1888-1894 гг. тщательно изучили серии щелочных металлов. Формула Бальмера может быть представлена в виде
n = А + Вm-2, m = 3,4,...
где n = 1/λ - волновое число. Кайзер и Рунге пытались представить линии щелочных металлов формулами:
n = А + Вm-2 + Сm-4
n = А + Вm-1 + Сm-2.
Ридберг в работах 1889-1900 гг., анализируя спектры щелочных металлов, показал, что спектры щелочных металлов распределяются в три серии (позже Бергман нашел четвертую - фундаментальную серию, или серию Бергмана): главную и две побочные. Линии этих серий могут быть представлены формулами.
Главная серия: 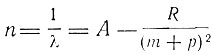
1-я побочная: 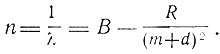
2-я побочная:
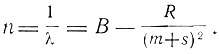

Серия Бальмера
Здесь введены позднейшие обозначения для постоянной R, получившей название постоянной Ридберга, и поправок р, d, s - поправок Ридберга. Ридберг показал, что линии могут быть представлены в виде разности двух членов - "термов". Так, линии главной и побочной серий могут быть представлены формулами:
Главная серия:
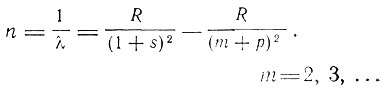
1-я побочная:
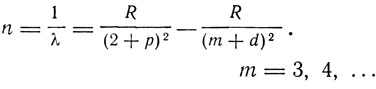
2-я побочная:
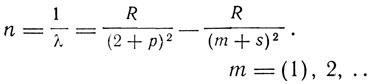
Постоянная Ридберга имеет значение 109 675, если для линии натрия принять длину волны равной λ = 5896,13 А0 (шкала Роуланда).
О своих работах по спектрам щелочных металлов Ридберг делал доклад на Парижском Международном конгрессе физиков 1900 г. Бор писал о результатах Ридберга: "На основе чрезвычайно точных измерений длин волн спектральных линий Роуландом и др. и после работ Бальмера и Шустера... общие спектральные законы чрезвычайно остроумным способом были систематизированы Ридбергом. Основным результатом тщательного анализа видимой серии линейчатых спектров и их взаимоотношений было установление того факта, что частота v каждой линии спектра данного элемента может быть представлена с необыкновенной точностью формулой v = Т' - Т", где T' и T" - какие-то два члена из множества спектральных термов Т, характеризующих элемент".
В этом высказывании Бора содержится уже и результат, найденный позже Ридберга В. Ритцем и известный под названием комбинационного принципа Ритца. Ритц в 1908 г. уточнил выражения для спектральных линий, данные Ридбергом. Он указал, что каждый из двух членов формулы, представляющей частоты спектральных линий, имеет как бы самостоятельное существование; из различных комбинаций этих членов (термов), относящихся к различным сериям, получаются частоты других линий спектра. Каждый терм характеризуется бегущим целым числом m и поправкой s, р или d, f, ... Ритц предложил записывать термы сокращенно в виде (mp), (ms) и т. д. Таким образом, частоты серий главной и побочных могут быть записаны в виде
vp = 1S - mP, m = 1, 2, 3, ... (главная серия)
vD = 2Р - mD, m = 3, 4, ... (1-я побочная)
vs = 2P - mS, m = 2, 3, ... (2-я побочная)
То обстоятельство, что частоты представляются такими формулами, было чрезвычайно трудно понять с точки зрения классической теории, поскольку с этой точки зрения, как указал в 1897 г. Рэлей, в спектральные законы должны входить квадраты частот. Положение сложилось весьма тягостное. "Никто,- писал в 1906 г. Стоней,- еще не достиг успеха, прокладывая путь от периодичностей, интенсивностей и других свойств спектральных линий элемента к такому движению электронов в молекулах, которое было бы способно в точности воспроизвести эти тонкие эффекты. Информация, даваемая нам природой, экспонирована в спектрах. Она записана в них, но таким языком, который никогда не был расшифрован".
|
ПОИСК:
|