Теория Бора

Таким образом, квантовые идеи все более и более проникали в атомную и молекулярную физику. Немудрено, что эти идеи захватили и молодого Бора. В своей уже цитировавшейся нами статье о Резерфорде он прямо пишет:

"Мои письма к Резерфорду, написанные осенью 1912 г., посвящены продолжавшимся усилиям выяснить роль кванта действия в электронном строении атома Резерфорда, включая сюда проблему молекулярной связи, а также вопросы излучения и магнитные эффекты. Однако,- продолжает Бор,- вопросы устойчивости, неизбежно возникающие при таких рассмотрениях, резко увеличивали трудности и вынуждали искать более надежную основу для решения проблемы. После многочисленных попыток использовать квантовые идеи в более строгой форме ранней весной 1913 г. мне пришло в голову, что ключом к разрешению проблемы атомной устойчивости, непосредственно приложимым к атому Резерфорда, являются изумительно простые законы, определяющие оптический спектр элементов".

Н. Бор

Здесь Бор имеет в виду, прежде всего, комбинационный принцип Ридберга-Ритца, согласно которому частоты спектральных линий представлялись в виде разности двух термов. Объединяя идею световых квантов Эйнштейна с моделью атома Резерфорда, Бор и пришел к мысли о возможности энергетического истолкования термов и к интерпретации испускания и поглощения излучения атомов как скачкообразного энергетического перехода.

При осуществлении этой идеи Бор столкнулся с одним затруднением. В 1897 г. американский астроном Эдвард Чарльз Пикеринг обнаружил в спектрах некоторых звезд серию, которую он интерпретировал как побочную "резкую" серию водорода. Одну из линий этой серии наблюдал английский спектроскопист Альфред Ф аул ер во время солнечного затмения 22 января 1898 г. в спектре солнечной хромосферы. В 1912 г. он нашел другие линии серии Пикеринга в лабораторных условиях в разрядной трубке, содержащей смесь водорода и гелия. Но включение линий Пикеринга и Фаулера в формулу Ридберга для спектра водорода требовало, чтобы число n в выражении термов принимало не только целые, но и полуцелые значения. А это не увязывалось с тем подходом к вычислениям термов, который был принят Бором. Зато чрезвычайно естественно было бы в соответствии с боровским подходом приписать эти линии спектру ионизованного гелия. "Если бы этот вывод подтвердился,- писал Бор,- можно было бы сделать первый шаг к установлению количественных связей между свойствами различных элементов на основе модели Резерфорда".

Титульный лист 26-го тома 'Phil. Mag.' 1913 г. со статьей Бора 'О строении атомов и молекул'

В марте 1913 г. Бор написал Резерфорду письмо, содержащее набросок его первой работы по строению атома. Резерфорд немедленно ответил письмом от 20 марта 1913 г. В этом письме он писал:

Я получил в полной сохранности Вашу работу и прочел ее с большим интересом, но мне хотелось бы еще раз тщательно просмотреть ее, когда у меня будет больше времени. Ваши мысли относительно причин возникновения спектра водорода остроумны и представляются хорошо продуманными, однако сочетание идей Планка со старой механикой создает значительные трудности для понимания того, что же все-таки является основой такого рассмотрения. Я обнаружил серьезное затруднение в связи с Вашей гипотезой, в котором Вы, без сомнения, полностью отдаете себе отчет; оно состоит в следующем: как может знать электрон, с какой частотой он должен колебаться, когда он переходит из одного стационарного состояния в другое? Мне кажется, что Вы вынуждены предположить, что электрон знает заблаговременно, где он собирается остановиться".

Сомнения Резерфорда очень показательны. Действительно, сочетание классической механики с идеями Планка кажется до известной степени противоестественным, а гипотеза недетерминированных квантовых скачков резко противоречила всему строю идей классической физики. Сам Бор называет замечание Резерфорда "очень дальновидным" и отмечает, что позднее оно стало центральным пунктом дискуссии вокруг идей квантовой теории.

Другое критическое замечание Резерфорда касалось размера статьи. Однако Бор не согласился ка ее сокращение и лично поехал в Манчестер к Резерфорду, где Резерфорд после длинных разговоров "согласился оставить все старые и новые вопросы в окончательном варианте статьи". Статья Бора, ставшая поворотным пунктом в развитии квантовой теории и атомной физики, появилась в 26-м томе журнала "Philosophical Magasin". Статья состояла из трех частей: первая была напечатана в июльском номере, вторая в сентябрьском, третья в ноябрьском номере журнала. В сноске перед каждой частью отмечалось, что статья представлена Резерфордом, и каждая статья Бора начиналась с указания на модель атома Резерфорда. Резерфорд и Бор стояли у истоков атомной теории, и это отразилось в только что указанных фактах.

Представляет интерес проследить "окружение" боровских статей. Из 90 с лишним статей и заметок тома почти треть составляют статьи по атомной и ядерной физике (преимущественно по радиоактивности). Здесь мы находим и знаменитую статью Мозли о спектрах рентгеновских лучей, и статью Д. Д. Томсона о "квантовом" варианте своей теории атома. Непосредственно за статьей Бора в июльском номере идет статья Крегора об образовании молекул элементов и их соединений с атомами, построенными по корпускулярно-кольцевой теории. Эта статья вся построена на основе идей томсоновского атома, тогда как статья Мозли уже примыкает к идеям Бора. Кроме того, в томе содержится статья Конвея об электромагнитной гипотезе происхождения линейчатых спектров. Все эти статьи характеризуют доборовскую и начальную боровскую ситуацию в атомной физике и мы должны позднее к ним вернуться.

Что касается ядерной физики и радиоактивности, то здесь видное место занимают работы Резерфорда и его сотрудников. Таковы статья "Анализ γ-лучей радия D и радия Е", написанная Резерфордом совместно с Ч. Ричардсоном, статья о рассеянии α-частиц в газе Резерфорда и Нэттела, об анализе α-лучей радия В и радия С Резерфорда и Робинсона, статья написанная Резерфордом совместно с Ч. Ричардсоном "Анализ γ-лучей тория и продуктов актиния", интересная заметка петербургского химика Г. Н. Антонова об уране Y. Среди других работ наиболее близко к атомной тематике подходят оптические работы знаменитого американского физика Роберта Вуда, которому принадлежат в этом томе три работы, в том числе две, посвященные резонансным спектрам, явлению, открытому Вудом и имеющему важное значение для квантовой теории атома. О резонансных спектрах говорит и Бор в своих статьях, разбирая проблему абсорбции света.

Еще до опубликования своей первой статьи Бор, посылая ее Резерфорду, обратил внимание на таинственную серию линий, наблюдавшихся Пикерингом и Фаулером, которые, как мы уже говорили, приписывали ее водороду. В свою очередь Бор приписывал ее ионизованному гелию, о чем и сообщил Резерфорду, указывая на желательность экспериментальной проверки этой идеи.

Резерфорд в уже цитировавшемся нами письме писал, что он очень заинтересовался предположениями Бора относительно спектра Фаулера, и сообщил об этом Эвансу, который намеревался поставить ряд опытов для проверки гипотезы Бора.

Однако пора перейти к самой статье Бора. Чтобы понять дух и содержание статьи, приведем выдержки из введения Бора ко всем трем частям статьи, предпосланного первой части. Вначале Бор говорит о моделях атома Резерфорда и Бора и указывает на различия между ними. "Принципиальное различие между атомными моделями Томсона и Резерфорда,- пишет Бор,- заключается в том, что силы, действующие на электрон в атомной модели Томсона, допускают определенные конфигурации и движения электронов, для которых система находится в устойчивом равновесии; но такие конфигурации, очевидно, не имеют места во второй модели атома. Характер обсуждаемого различия наиболее ясно виден, если принять во внимание то обстоятельство, что среди величин, характеризующих первый атом, имеется величина - радиус положительной сферы,- которая имеет размерность длины и тот же порядок величины, как и линейные размеры атома, в то время как длина не фигурирует среди величин, характеризующих второй атом: заряда и массы электронов и положительного ядра; эта длина не может быть и определена из этих величин".

Первая страница статьи Бора 'О строении атомов и молекуль'

Далее Бор указывает на успехи квантовой теории излучения, теплоемкости, фотоэффекта и пишет: "В результате обсуждения этих вопросов выявилось общее убеждение в неадекватности классической электродинамики для описания систем атомных размеров (здесь Бор делает ссылку на доклады Сольвеевского конгресса "Теория излучения и кванты", 1911). Каковы бы ни были изменения законов движения электронов, кажется необходимым ввести в эти законы величину, чуждую классической электродинамике - постоянную Планка, или, как ее часто называют, элементарный квант действия. Благодаря введению этой величины вопрос об устойчивости конфигурации электронов существенно меняется, так как эта постоянная имеет такую величину и размерность, что она вместе с массой и зарядом частицы определяет длину требуемой величины".

Определяя затем задачи своей работы, Бор пишет: "Эта статья является попыткой показать, что применение упомянутой выше идеи к модели атома Резерфорда может быть основой теории строения атомов. Далее будет показано, что, исходя из этой теории, мы можем прийти к теории строения молекул.

В настоящей статье обсуждается механизм связывания электронов положительным ядром в его отношении к теории Планка. Она имеет целью показать, что с этой точки зрения возможно объяснить простым образом закон линейного спектра водорода. Далее приводятся аргументы в пользу главной гипотезы, на которой основаны рассуждения, содержащиеся в последующих частях. Я хочу здесь выразить мою благодарность проф. Резерфорду за его благожелательное отношение и воодушевляющий интерес к этой работе".

Такова программа Бора. Нельзя отказать ей в смелости. Бор пытается построить на основе квантовой гипотезы теорию строения не только простых атомов типа водородного атома, но и других более сложных атомов - даже молекул. Это может означать только то, что Бор понял, что идея квантов является ключом к пониманию структуры атомов и молекул. И в этом отношении он не ошибся. Однако конкретное выполнение этой обширной программы в этой его первой статье, разумеется, было еще далеко от завершенности. Это только начало большого пути атомной физики, и в том, что Бор положил это начало, и заключается его бессмертная заслуга в истории физики.

Бор начинает свой анализ с рассмотрения простейшей системы: положительно заряженного массивного ядра и электрона, описывающего замкнутые орбиты вокруг ядра. Для электрона принимается, что его масса мала по сравнению с массой ядра, а скорость мала по сравнению со скоростью света. Первое позволяет считать центром системы центр ядра, второе - применять нерелятивистскую классическую механику.

Как-то сразу, без особого подчеркивания, Бор пишет: "Предположим в качестве первого допущения, что отсутствует энергия излучения. В этом случае электрон будет описывать стационарные эллиптические орбиты". Он не объясняет, почему отсутствует, вопреки классической электродинамике, энергия излучениями просто принимает, что ее нет. Тогда энергия, затрачиваемая на то, чтобы привести электрон из бесконечности на орбиту с большой полуосью 2а, по которой электрон вращается с частотой (не круговой!) со, будет W и частота ω и ось 2а связаны с W выражениями:

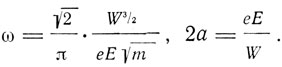
(1)

Здесь e - заряд электрона, Е - заряд ядра, m - масса электрона. Далее оказывается, что среднее значение кинетической энергии электрона за период равно W.

Затем Бор рассматривает, что случилось бы, если система начала излучать. В этом случае W будет возрастать до бесконечности, а электрон будет приближаться к ядру. Очевидно, что реальные атомные системы не ведут себя таким образом. "Прежде всего,- пишет Бор,- реальные атомы в своем постоянном состоянии кажутся имеющими абсолютно неизменные размеры и частоты. Кроме того, если мы рассмотрим какой-либо молекулярный процесс, в результате которого оказывается излученной определенная энергия, имеющая величину, характерную для рассматриваемой системы, то эта система снова возвращается в устойчивое состояние равновесия, в котором состояния между частицами будут того же порядка величины, что и до процесса".

Вот эта-то удивительная устойчивость атомных систем и находится в противоречии с моделью Резерфорда, если последнюю описывать классической электродинамикой. Здесь Бор и привлекает гипотезу Планка, согласно которой излучение совершается целыми квантами.

Бор рассматривает процесс образования простейшей системы, состоящей из положительного ядра и электрона, вращающегося по круговой орбите. Предполагается, что в начале процесса электрон находится на чрезвычайно большом расстоянии от ядра и обладает ничтожно малой скоростью. В результате взаимодействия с ядром электрон переходит на круговую стационарную орбиту. В этом процессе, по гипотезе Бора, он излучал энергию частоты, равной половине частоты его обращения по окончательной орбите. При этом, по гипотезе Планка, величина излученной энергии

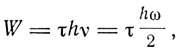
(2)

где τ - целое число, W - кинетическая энергия, которой электрон обладает в конечном состоянии, определяемая формулой (1). Вводя из формул (1) величины со и а, получаем

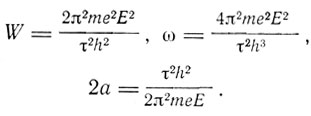
(3)

Давая τ различные значения, мы получаем набор значений W, ω, а, соответствующий набору возможных конфигураций системы. Эти конфигурации "будут соответствовать состояниям системы, в которых энергия не излучается, т. е. состояниям, которые остаются стационарными до тех пор, пока система не возмущается извне".

Наиболее устойчивому состоянию соответствует состояние, в котором W максимально, что соответствует значению τ = 1. Для этого состояния Бор получает, используя значения e = 4,7*10^-10,

Эти значения соответствуют линейным размерам атома, оптических частот и ионизационного потенциала.

Бор указывает, что согласие между наблюдаемыми значениями частот и размеров атомов и вычисленными значениями по способу, аналогичному приведенному, неоднократно обсуждалось. Он указывает на вычисления А. Э. Гааза (1910), А. Шидлова (1911), Э. Вертгеймера (1911), Ф. Линдемана (1911), Ф. Габера (1911), напоминая при этом о попытке Гааза вычисления h на основе модели Томсона.

Далее Бор упоминает о работе Никольсона (1912), о которой, равно как и о работе Гааза, говорилось выше. Он пишет по поводу теории Никольсона: "Блестящее согласие между вычисленными и наблюдаемыми значениями отношений длин волн спектров является сильным аргументом в пользу теории Никольсона". Вместе с тем он указывает на возражения против этой теории. Никольсон отождествлял частоту излучения с частотой колебаний механической системы, но системы, в которых частота является функцией энергии, не могут испускать конечного количества однородного излучения, так как при излучении частота их будет меняться. Кроме того, системы, рассчитанные Никольсоном, будут неустойчивы при некоторых формах колебаний. И наконец, как замечает Бор, теория Никольсона не может дать отчета о сериальных законах Бальмера и Ридберга. Поэтому Бор снова возвращается к своим предположениям, которые он формулирует еще раз следующим образом:

"(1) ... динамическое равновесие систем в стационарных состояниях можно рассматривать с помощью обычной механики, тогда как переходы системы между различными стационарными состояниями нельзя рассматривать на этой основе.

(2) ... последний процесс влечет за собой испускание однородного излучения, для которого соотношение между частотой и величиной излучаемой энергии будет тем, какое дает теория Планка".

Комментируя первое допущение, Бор указывает, что оно является до известной степени притянутым, поскольку обычная механика применима только к средним значениям движения электронов. Но при расчетах стационарных состояний, когда нет относительного смещения частиц, различие между средними и действительными значениями исчезает. Что же касается второй гипотезы, то Бор не скрывает ее противоречия с обычной электродинамикой, однако указывает, что эта гипотеза необходима для описания экспериментальных фактов.

В следующем параграфе статьи Бор переходит к обсуждению линейного спектра водорода. Для водорода заряд ядра Е равен заряду электрона е, и поэтому выражение для энергии, данное в формулах (3), принимает вид

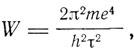
где τ - целое число. Отсюда величина энергии, излучаемой при переходе системы из состояния, для которого τ = τ₁ в состояние, для которого τ = τ₂, будет

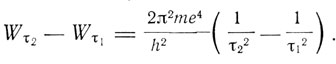
Полагая, что излучается один квант энергии hv, т. е. что W_τ2 - W_τ1 = hv, получим

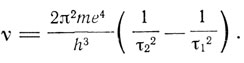
Для τ₂ = 2 получается серия Бальмера, для τ₂ = 3 - серия в инфракрасной области, наблюденная Пашеном в 1908 г. и существование которой подозревал Ритц. Для τ₁ = 1, а также τ₂ = 4, 5, ... получаются еще не известные во времена Бора серии в ультрафиолетовой области. Вычисление постоянной перед скобками с помощью значений

дает

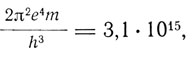
тогда как экспериментальное значение равно 3,290*10¹⁵. "Согласие между теоретическим и наблюденным значениями,- пишет Бор,- находится в пределах неточности, обусловленной экспериментальными ошибками в определении констант, входящих в выражение для теоретической величины".

Бор указывает далее, что тот факт, что в лабораторных условиях не удавалось получить более 12 линий серии Бальмера, тогда как в спектрах некоторых небесных тел наблюдалось 33 линии, также говорит в пользу теории. Для больших τ размеры орбит становятся очень большими, и для получения линий, соответствующих этим высоким значениям τ, требуется очень высокая степень разреженности газа. Но для получения линий высокой интенсивности, наоборот, должно быть очень много атомов в исследуемом пространстве. "Если теория верна, то мы, таким образом, никогда не можем наблюдать в экспериментах с вакуумными трубками линии, соответствующие высоким номерам серии Бальмера в спектре испускания водорода; однако возможно наблюдать эти линии при исследованиях спектра поглощения в этом газе". Бор переходит затем к обсуждению спектра, найденного в 1896-1897 гг. Г. Пикерингом в спектре звезды ζ-Puppis, а также Фаулером в 1912 г. в вакуумных трубках, заполненных смесью водорода и гелия. Эти линии приписывались названными исследователями водороду. Бор утверждает, что их следует приписывать ионизованному атому гелия, для которого, полагая в (3) E = 2e, получаем

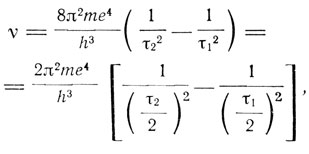
т. е. те самые линии, которые наблюдали Пикеринг и Фаулер. Линии Фаулера получаются, если положить τ₂ = 3, а Пикеринга, если положить τ₂ = 4. Каждая вторая из этих линий тождественна линиям серии Бальмера, которые наблюдались также и в опытах Фаулера и назывались им "резкой" серией водородного спектра.

Переходя к спектрам других элементов, Бор устанавливает, что по принципу Ридберга-Ритца частоты линий спектра элемента всегда могут быть представлены в виде разности

где τ₁, τ₂ - целые числа, а функции F₁, F₂, F₃,... могут быть приближенно представлены выражениями

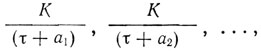
причем К - универсальная постоянная, входящая в выражение спектра водорода (ее теперь называют постоянной Ридберга). Такое выражение для линий в рассматриваемых спектрах подсказывает мысль, что происхождение линий в них аналогично происхождению линий в водородном спектре. Правда, в случае многоэлектронных систем задача будет очень сложной. Вместе с тем константа К будет фигурировать и в этих сложных спектрах. Бор это показывает тем, что система, состоящая из отдельного электрона, ядра и остатка электронов, будет аналогична водородному атому. Таким образом, для больших τ

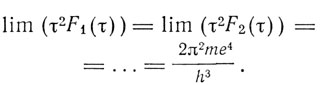
Затем Бор переходит к обсуждению своего основного постулата, что испущенная энергия

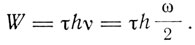
(2)

Предположение, что сразу излучается несколько квантов, кажется сомнительным, "поскольку один испущенный квант изменяет частоту". Для обсуждения этого вопроса Бор вводит вместо (2) более общее соотношение W = f(τ)*hω. В этом случае вместо уравнений (3) получается

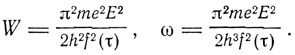
Если предположить, что величина энергии, испущенной при переходе из состояния τ = τ₁ в состояние τ = τ₂, равна hv, то отсюда получаем

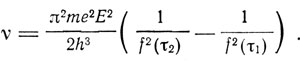
Отсюда видно, что для получения выражения типа бальмеровского надо положить f(τ) = cτ. Для определения с Бор рассматривает переход из состояния τ = N в состояние τ = N-1. Тогда частота испускаемого излучения

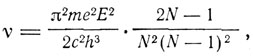
и для частот обращения электрона до и после излучения получаем

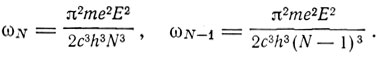
При большом N отношение ^ω_N/_ωN-1∼1, и согласно обычной электродинамике следует ожидать, что и отношении ^v/_ωN∼1, т. е. ²/_c∼1 и c≅¹/₂ Полагая f(τ) = ^τ/₂, приходим к прежнему выражению (2). Если же рассматривать переход между состояниями τ = N и τ = N - n, где N>>n, то с тем же приближением получаем f(τ) = ^τ/₂, v = nω. Эта частота соответствует частоте n-го обертона в разложении Фурье. "Мы приходим, таким образом, к предположению,- пишет Бор,- что интерпретация уравнения (2) заключается не в том, что различным стационарным состояниям соответствует испускание разного числа квантов энергии, а в том, что частоты энергии, излучаемые во время перехода системы из состояния, в котором энергия еще не излучалась, к одному из различных стационарных состояний, равны различным кратным от ^ω/₂, где ω - частота обращения электрона в рассматриваемом состоянии". В этих рассуждениях Бора мы усматриваем зародыш его будущего принципа соответствия. Вообще же следует сказать, что в истории новая истина никогда не рождается сразу в готовом виде. Автор новой идеи, как правило, вначале еще продолжает пользоваться старыми привычными представлениями. Так, Максвелл формулировал свои идеи в механических образах, исходя из сомнительной аналогии вектора-потенциала с механическим импульсом. И Герц не сразу перешел в "чистый эфир", а сначала связывал контур проводящим мостиком с излучателем. Так, Бор в своей первой статье тесно связан с механическим образом электрона, вращающегося по замкнутой орбите, и частота его обращения все еще доминирует в спектральных формулах. Новое рождается в старой оболочке.

Применяя принципы обычной механики, Бор приходит к замечательной особенности стационарных орбит. Обозначая угловой момент электрона относительно ядра через M, причем πM = ^T/_ω, где Т - кинетическая энергия электрона, а ω - его частота (число обращений в секунду) и для круговой орбиты T = W, и условие W = τh^ω/₂ дает M = τM₀, где M₀ = ^h/_2π = 1,04*10^-27.

Таким образом, условие стационарности орбит может быть выражено так: "Угловой момент электрона относительно ядра в стационарном состоянии равен целому кратному от универсального значения, не зависящего от заряда ядра".

Мы видим, что действительный путь Бора резко отличается от того, который ныне описывается в учебниках. Условие квантования вращательного момента для стационарных орбит было не постулатом, как это представляет современное изложение теории Бора, а следствием постулата, что частота излучения равна половине угловой частоты вращения на стационарной орбите. Бор отмечает, что на важное значение углового момента при обсуждении атомных систем указал Никольсон. Он отмечает также, что обычное "постоянное" состояние атома соответствует значению τ = 1.

Р. Вуд

Замечательными являются рассуждения Бора об абсорбции, которым посвящен четвертый параграф его статьи. Он вводит идею резонансного поглощения, которую формулирует следующим образом: "... мы должны принять, что система, состоящая из ядра и электрона, вращающегося вокруг него, может при некоторых обстоятельствах поглощать энергию частоты, равной частоте однородного излучения, испускаемого в течение перехода между двумя стационарными состояниями. Допустим, что мы рассматриваем излучение, испущенное во время перехода системы между стационарными состояниями А₁ и A₂, соответствующими значениям τ, равным τ₁ и τ₂, причем τ₁>τ₂. Так как необходимое условие испускания рассматриваемого излучения заключалось в наличии систем в состоянии A₁, то мы должны принять, что необходимым условием поглощения является наличие систем в состоянии А₂". Бор подчеркивает, что такая точка зрения на поглощение излучения расходится с обычной электродинамикой, так как система может поглощать излучение, частоты которого отличны от классической частоты колебаний электрона. Он указывает, что эти теоретические соображения подтверждаются опытами Р. Вуда 1911 г. по поглощению света парами натрия. Здесь это резонансное, как его теперь называют (Бор этого термина еще не употреблял), поглощение, как указывает Бор, не является истинным поглощением, а только рассеянием первичного излучения.

Бор считает, что и возникновение рентгеновских лучей, а следовательно, столкновение свободного и связанного электронов также подчиняются квантовым законам, а не обычной электродинамике.

Он вводит принцип, согласно которому сталкивающиеся электроны - свободные и связанные - как до столкновения, так и после него находятся в определенных механических состояниях. Из этого принципа вытекает, что при столкновении "связанный электрон не может потреблять энергии меньше, чем разность энергий между двумя последующими стационарными состояниями, и, следовательно, свободный электрон, сталкивающийся с ним, не может терять энергии, меньшей этой величины".

Этот вывод Бора был блестяще подтвержден классическими опытами Франка и Герца 1914 г. И сам Бор, подчеркивая провизорный и гипотетический характер своих рассуждений, не сомневался в том, что "обобщение теории стационарных состояний, может быть, будет в состоянии дать простую основу для описания многих экспериментальных фактов, не объяснимых с помощью обычной электродинамики".

В заключительном параграфе первой части своей статьи Бор рассматривает "постоянное" ("permanent") состояние атома. Для системы, состоящей из ядра и электрона, т. е. водородного атома, это состояние соответствует значению углового h момента электрона, равному ^h/_2π.

Бор указывает, однако, что это состояние трудно наблюдать на опыте, поскольку в обычных условиях атомы водорода связаны в молекулы. Поэтому он переходит к рассмотрению более сложных атомов, содержащих несколько электронов. Здесь он, примыкая к идеям Д. Д. Томсона, считает стационарным состоянием то, в котором электроны распределены по кольцам. Тогда возникает трудный вопрос об устойчивости системы.

Однако на первых порах Бор обходит этот вопрос и рассматривает размеры и частоту такой системы электронов. Считая кольцо окружностью радиуса а, на которой размещены на равных угловых расстояниях друг от друга п электронов, Бор пишет выражение потенциальной энергии такой системы:

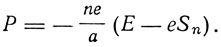
Здесь Е - заряд ядра, а

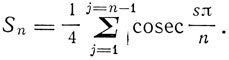
Условие динамического равновесия системы заключается в равенстве центробежной силы радиальной силе притяжения:

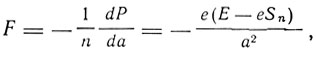
а именно

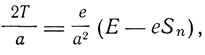
где Т - кинетическая энергия электрона. Из этого равенства

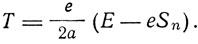
Отсюда

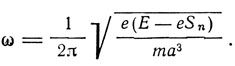
Полное значение энергии, которое необходимо сообщить системе, чтобы удалить электроны от ядра и друг от друга,

т. е. равно полной кинетической энергии электронов. Отличие этой формулы от формулы для одного электрона заключается в замене Е на Е - eS_n. Поэтому так же, как и в случае одного электрона, энергия, испускаемая при образовании системы, равна кинетической энергии электронов. По аналогии с системой, состоящей из одного электрона, приходим здесь к представлениям о существовании стационарных состояний, в которых кинетическая энергия равна τh^ω/₂. Конфигурации, при образовании которой испускается наибольшее количество энергии, соответствует τ = 1. Это и есть постоянное состояние атома, причем каждый из электронов обладает угловым моментом ^h/_2π.

Далее Бор останавливается на вопросе устойчивости системы, примыкая к исследованиям Томсона и Никольсона. Эти рассуждения об устойчивости мы опустим. Бор заканчивает свою статью следующей теоремой: "В каждой системе, содержащей электроны и положительные ядра, в которой ядра покоятся, а электроны движутся по круговым орбитам со скоростью, малой по сравнению со скоростью света, кинетическая энергия численно равна половине потенциальной энергии". И наконец, Бор в общем виде формулирует признак постоянного состояния системы: "В любой молекулярной системе, содержащей положительные ядра и электроны, в которой ядра покоятся друг относительно друга, а электроны движутся по круговым орбитам, угловой момент каждого электрона относительно центра его орбиты для постоянного состояния системы будет равен ^h/_2π, где h - постоянная Планка". Эта конфигурация будет устойчивой, если полная энергия системы будет меньше, чем в любой соседней конфигурации, удовлетворяющей тому же самому условию углового момента электронов. Таково содержание первой части статьи Бора.

Во второй части статьи Бор рассматривает многоэлектронные атомы. Эта часть начинается с упоминания о модели Резерфорда и гипотезы ван ден Брука о равенстве 4jH-сла электронов порядковому номеру элемента: "Все эксперименты подчеркивают гипотезу (в этом месте Бор ссылается на статью А. ван ден Брука 1913 г.), что действительное число электронов в атоме, за немногими исключениями, равно числу, которое указывает положение соответствующего элемента в рядах элементов, расположенных в порядке возрастания атомного веса".

Во втором параграфе этой части статьи Бор рассматривает устойчивые конфигурации системы. Электрон заряда е и массы m вращается по круговой орбите радиуса а под действием радиальной силы, закон которой выражается формулой ^e2/_a²*F, где F вообще зависит от а и для водородного атома равно 1. Условие динамического равновесия дает

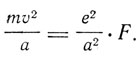
Если орбита устойчива, то ее угловой момент равен ^h/_2π. Следовательно,

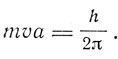
Из этих двух уравнений получаем

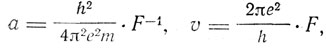
(1)

и

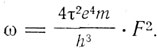
(2)

Этот вывод параметров устойчивого движения хорошо известен из учебников для водородного атома, когда F = 1. В случае кольца из "электронов, вращающихся вокруг ядра с зарядом Ne,

где

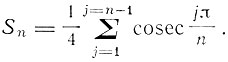
Ссылаясь на теорему, приведенную в конце предыдущей статьи, Бор пишет выражение для полной кинетической энергии электронов, которая по этой теореме равна энергии, испущенной в процессе образования системы:

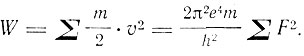
(3)

Подставляя сюда данные для

и

получаем

При этом F должно быть мало по сравнению с 150.

Бор рассматривает далее вопрос об устойчивости системы. Для смещений, происходящих в плоскости кольца, устойчивость обеспечивается универсальным постоянством углового момента. Для смещений, перпендикулярных плоскости кольца, Бор утверждает следующее: "Если смещения системы производятся бесконечно медленно, то движение электронов в любой момент будет параллельно первоначальной плоскости кольца и угловой момент каждого электрона вокруг центра его орбиты будет, очевидно, равен его первоначальному значению". Здесь для вычисления колебаний электронов перпендикулярно к плоскости ядра и, следовательно, для решения вопроса об устойчивости пригодна обычная механика, что было показано еще Никольсоном. Бор рассматривает возможные системы колец и их устойчивость. Его результаты можно иллюстрировать примерами систем с небольшим числом электронов, которое он разбирает в третьем параграфе статьи. При этом он вводит символическое обозначение N(n₁,sub>2, n₃, ...), где N - полное число электронов (заряд ядра), n₁ - число электронов в первом, самом внутреннем кольце радиуса a₁, n₂ - число электронов во втором кольце радиуса а₂ и т. д. Величина энергии, испущенной при образовании данной конфигурации, обозначается через

Для водорода N = 1. Конфигурация 1 (1) характеризуется числами

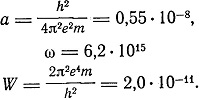
Для ^W/_e получаем число 0,043 ед. CGSE = 13 в, значение ионизационного потенциала, совпадающее с найденным Томсоном из опытов с положительными лучами.

Бор показал и возможность конфигурации 1 (2), т. е. отрицательного иона водорода, для которого а = 1,33 а₀, (ω = 0,563 ω₀, W = 1,13 W₀, где а₀, ω₀, W₀ - величины, относящиеся к конфигурации 1 (1). Дважды отрицательного иона водорода 1 (3), как следует из энергетических соображений, быть не может. Затем Бор переходит к описанию гелия, для которого N = 2. Для конфигурации, соответствующей положительно заряженному однократному иону гелия (конфигурация 2 (1)), Бор получает

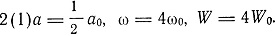
Что касается нейтрального гелия, то Бор пишет, что можно с полной уверенностью допустить существование стабильной конфигурации:

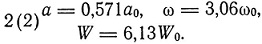
Энергия, необходимая для отрыва одного электрона,

Отсюда ионизационный потенциал гелия равен 2,13^W₀/_e = 27 в, в то время как опыты Франка и Герца 1913 г. дали значение 20,5 в. Бор считает, что теория по порядку величины дает согласие с опытом. Далее Бор показывает, что конфигурация 2 (3) энергетически менее выгодна для конфигурации 2(2) и, следовательно, атом гелия не может приобретать отрицательный заряд. Для лития N = 3 Бор пишет по аналогии с водородом и гелием спектральную формулу

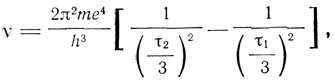
одновременно указывая, что этот спектр можно наблюдать только в исключительных случаях.

Для постоянного состояния атома лития, потерявшего два электрона (ион лития с двойным положительным зарядом), Бор получает

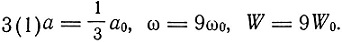
Для атома лития с одним положительным зарядом

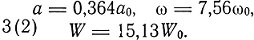
Так как W[3(2)] - W[3(1)] = 6,13 W₀, то Бор утверждает, что два электрона в атоме лития более сильно связаны, чем электроны в атоме гелия. Для нейтрального атома лития по химическим соображениям следует ожидать конфигурации 3(2, 1) причем

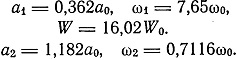
Бор считает вероятной и конфигурацию 3(3), для которой W = 17,61 W₀, и для отрицательного иона конфигурацию 3(2,2). Вместе с тем Бор сознается, что мы еще не располагаем достаточными сведениями об атомных состояниях.

Таким же образом Бор обсуждает конфигурацию бериллия 4(2,2), считая, что она в своем образовании проходила следующие стадии: 4(1), 4(2), 4(2,1) и наконец 4(2,2). Вместе с тем он не считает исключенной и конфигурацию 4(4).

Обсуждая системы с многими электронами, Бор приходит к выводу, что кольца с равными числами электронов имеют тенденцию сливаться, и поэтому числа электронов ЕО внутренних кольцах будут 2, 4, 8, ... Он указывает, что эта гипотеза сильно поддерживается периодичностью в системе элементов, в которой число 8 является одним из основных периодов. Бор рассматривает конфигурацию электронов и выписывает возможные, по его мнению, распределения электронов для элементов от 1 до 24. Так, уже в первой своей статье Бор предпринял попытку истолкования периодической системы элементов.

В заключение своей статьи Бор рассматривает возникновение рентгеновских лучей, которые, по гипотезе Томсона, возникают при вырывании электрона из внутренних колец атома, а также возникновение радиоактивного излучения. Испускание α- и β-частиц происходит из самого ядра и сопровождается перестройкой атома в соответствии с законом смещения Содди-Фаянса.

Бор резюмирует основную идею этой части своей статьи следующими словами: "В настоящей статье была сделана попытка показать, что применение планковской теории излучения к модели атома Резерфорда посредством введения гипотезы универсального постоянства углового момента связанных электронов приводит к результатам, находящимся в согласии с экспериментом".

В третьей части своей статьи, носящей заглавие "Системы, содержащие несколько ядер" и опубликованной в ноябрьской книжке журнала "Philosofical Magazin", Бор рассматривает строение молекул. Обсуждая принцип образования молекул, Бор приходит к выводу, что молекула может образоваться посредством взаимодействия систем, каждая из которых состоит из ядра, связавшего некоторое число электронов. Тот процесс связывания электронов ядром, который играл доминирующую роль в первых двух частях статьи Бора, не подходит для образования молекул, ибо нельзя удержать совместно положительные ядра атомов, образующих молекулу. Таким образом, Бор и приходит к изложенной выше идее. Свою теорию образования молекул Бор развивает, прежде всего, на простейшем случае системы, содержащей два ядра и кольца электронов, вращающихся вокруг оси, соединяющей ядра. Результат расчета такой системы, по мнению Бора, дает указание на то, какие конфигурации могут быть ожидаемы в более сложных случаях. Расчет равновесных конфигураций производится на основе обычной механики, но для определения абсолютных размеров системы и для ее устойчивости необходим квантовый принцип, согласно которому угловой момент каждого электрона относительно его центра равен универсальному значению ^h/_2π. Устойчивость же определяется тем условием, что полная энергия системы меньше, чем для любой ближайшей конфигурации, удовлетворяющей тому же условию углового момента.

Рассматривая систему из двух положительно и одинаково заряженных ядер и кольца электронов, вращающихся вокруг линии, соединяющей ядра, Бор находит выражения для стационарной конфигурации, т. е. соотношение между расстоянием между ядрами и радиусом кольца в зависимости от заряда ядра и числа электронов, а из квантового условия для углового момента находит радиус кольца и угловую скорость вращения электронов, равно как и значение кинетической энергии электрона.

В частности, для водородной молекулы соотношение между расстоянием между ядрами 2b и диаметром кольца 2а оказывается равным b = ¹/_√3a. При этом радиус электронного кольца, частота обращения электронов со и их кинетическая - энергия W связаны с радиусом орбиты водородного атома а₀, угловой скоростью электрона в водородном атоме ω₀ и его энергией W₀ соотношениями

Поскольку W>2W₀, то водородная молекула образуется из атомов водорода с выделением энергии, величина этой энергии (W-W₀)*N, где N = 6,2*10²³ (число Авогадро), по подсчетам Бора, равна 6*10⁴ кал, тогда как, по измерениям Лэнгмюра 1912 г., величина энергии, выделяющейся при образовании грамм-молекулы водорода, составляет 13*10⁴ (по современным данным, 10,4*10⁴). Бор рассматривает также возможность образования системы из двух ядер и трех электронов (отрицательный молекулярный водородный ион) и двух ядер и одного электрона (положительный молекулярный водородный ион) и показывает, что вторая комбинация неустойчива, а появление таких ионов в опытах Том-сона с положительными лучами следует объяснить специфическими условиями, при которых наблюдаются такие системы.

Бор рассматривает процесс образования молекулярных систем, например образование водородной молекулы из атомов водорода. С этой целью он рассматривает бесконечно медленное сближение атомов, плоскости орбит которых параллельны друг другу. Это сближение происходит до тех пор, пока не образуется устойчивая конфигурация, полная энергия которой будет меньше, чем энергия двух отдельных атомов. Наконец, Бор рассматривает и более сложные молекулы.

В заключительных замечаниях Бор указывает, что им во всех трех частях статьи была предпринята попытка "развить теорию строения атомов и молекул на основе идей, введенных Планком для описания излучения черного тела, и теории строения атома, предложенной Резерфордом для объяснения рассеяния α-частиц веществом".

Бор перечисляет основные допущения, которые им вводились для решения поставленной задачи. Вот эти допущения:

1. "Что энергия излучения не испускается (или поглощается) непрерывно способом, принятым в обычной электродинамике, а испускается только во время перехода системы из одного "стационарного" состояния в другое.
2. Что динамическое равновесие системы в стационарных состояниях управляется обычными законами механики, но эти законы неприменимы для переходов системы из одного стационарного состояния в другое.
3. Что излучение, испускаемое во время перехода системы из одного стационарного состояния в другое, однородно и что соотношение между частотой v и величиной излученной энергии дается уравнением Е = hv, где h - постоянная Планка.
4. Что различные состояния простой системы, состоящей из электрона, вращающегося вокруг положительного ядра, определяются условием, что отношение между полной энергией, испускаемой в процессе образования конфигурации, и частотой обращения электрона есть целое кратное ¹/₂h. Принимая, что орбита электрона круговая, мы видим, что это предположение эквивалентно предположению, что угловой момент электрона вокруг ядра равен целому кратному ^h/_2π.
5. Что "постоянное" состояние любой атомной системы, т. е. состояние для которого испущенная энергия максимальна, определяется условием, что угловой момент каждого электрона относительно его орбиты равен ^h/_2π".

Эти предположения, будучи применены к модели атома Резерфорда, и дают возможность Бору объяснить спектральные закономерности Бальмера и Ридберга. Вместе с тем Бор полагает, что ему удалось объяснить основные черты строения атомов различных элементов и образования молекул химических соединений в удовлетворительном согласии с экспериментом. Он заканчивает свою статью следующими словами: "Тесная связь настоящей теории с современной теорией черного излучения и удельной теплоемкости очевидна. Кроме того, поскольку по обычной электродинамике магнитный момент, обусловленный вращением электрона по круговой орбите, пропорционален угловому моменту, мы должны ожидать близкой связи с теорией магнетонов, предложенной Вейсом. Развитие обстоятельной теории теплового излучения и магнетизма на основе настоящей теории требует, однако, дополнительных предположений о поведении связанных электронов в электромагнитном поле. Автор надеется позднее вернуться к этим вопросам". Так, Бор намечает программу дальнейшего развития своей теории.