Эффект Штарка

В 1913 г. И. Штарк открыл эффект расщепления спектральных линий в электрическом поле. В том же году Э. Варбург попытался истолковать этот эффект, опираясь на теорию Бора, основные положения которой он формулирует в следующих постулатах:

"Постулат 1. Вращающийся электрон не излучает. Излучение, по г. Бору,- процесс, происходящий во время связывания электрона.

Постулат 2. Представим себе электрон, покоящийся на далеком расстоянии от ядра. Когда он затем движется к ядру, часть его потенциальной энергии расходуется на вращательное движение вокруг ядра, часть превращается в излучение, испускаемое квантами. По окончании этого процесса электрон вращается вокруг ядра без излучения.

Постулат 3. Возможны различные процессы подобного рода, отличающиеся друг от друга числом τ испущенных квантов энергии, причем τ может принимать значения 1, 2, 3, ... Тем самым определяется ряд окружностей, каждой из которых соответствует один из этих процессов".

Эти окружности определяются значениями

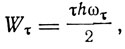
где W_τ - кинетическая энергия τ-й окружности, частота обращения электрона по ним, равно как и радиусы окружностей, определяются равенством

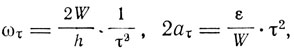
где ε - заряд электрона.

Далее Варбург формулирует пятый постулат:

"Постулат 5. Пусть далее возможны процессы, при которых система от одной окружности a_n переходит к другой a_m (m>n), испуская только один квант hv, это будут как раз те процессы, которым соответствуют наблюдаемые спектральные линии". Отсюда получается формула Бальмера

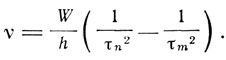
По-видимому, изложение Варбурга является первым изложением теории Бора, как она дана в первой боровской статье. Чтобы объяснить явление Штарка, Варбург прежде всего устанавливает, что внутреннее электрическое поле в атоме значительно превосходит внешнее приложенное поле. Поэтому он принимает, что орбиты атома остаются невозмущенными и определяются боровскими условиями. Однако приложенное поле изменяет энергию, появляется добавочный член ±Eεa_m и согласно условию частот Бора частота изменяется. По вычислениям Варбурга изменение длины волны для m-го состояния, определяемого номером τ_m, составляет

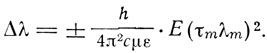
Это означает, что линии остаются теми же самыми, как в первоначальном спектре, но испытывают симметричное расширение на величину 2Δλ_m.

Однако результат, полученный Штарком для водородных линий, гласит:

1. Под действием электрического поля в поперечном поле линии Н_β и H_γ разлагаются на пять компонент, из которых три средние колеблются параллельно, две крайние - перпендикулярно электрическому полю. Средняя компонента параллельного триплета приблизительно совпадает с нерасщепленной линией.
2. Расщепление спектральной линии (расстояние между компонентами), измеренное в длинах волн, оказывается в первом приближении пропорциональным первой степени напряженности поля.

Эти результаты первых опытов Штарка, процитированные в статье Варбурга, очевидно, не совпадают с результатом теории Варбурга. Отсюда Варбург делает вывод, что теория Бора для описания явлений Штарка и Зеемана нуждается в видоизменении и расширении^*. Впервые явление Штарка на основе теории Бора было истолковано К. Шварцшильдом и П. С. Эпштейном в 1916 г. на основе волновой механики - Э. Шредингером в 1926 г. и матричной квантовой механики - В. Паули в том же, 1926 г.

^* (Бор в сноске к своей статье 1914 г. "О влиянии электрических и магнитных полей на спектральные линии" кратко излагает результаты Э. Варбурга.)

Таковы были первые шаги теории Бора. Несмотря на очевидную "сыроватость" и уязвимость этой теории, историческое значение ее огромно: она открыла путь в мир атомных явлений. Первый шаг, сделанный Бором, оказался далеко не последним, и после трудных поисков и сомнений физика создала замечательную квантовую теорию атомных явлений. Но это случилось уже. спустя 12-14 лет после появления первой статьи Бора.