Модели Томсона и Конвея

В статье "О строении атомов" (речь на съезде в Британской ассоциации 11 сентября 1913 г.) Д. Д. Томсон пытался связать свою модель атома с квантовыми свойствами атомных систем. Говоря об этих квантовых свойствах, Томсон указывал на то, что соотношение Планка ε = hv обычно рассматривается как "указание на то, что лучистая энергия имеет молекулярную структуру". По мнению Томсона, то же самое вытекает и без этой гипотезы о структуре излучения, с помощью особого представления о механизме атома, трансформирующего лучистую энергию в кинетическую. "Соотношение Планка,- пишет Томсон,- скорее зависит от свойств атома, являющегося агентом, преобразующим энергию, чем от наличия структуры в самой энергии". Томсон предполагает наличие в атоме двоякого рода сил:

1. радиальной отталкивающей силы, меняющейся обратно пропорционально кубу расстояния от центра и распределенной по всему пространству атома,
2. радиальной притягивающей силы, изменяющейся обратно пропорционально квадрату расстояния от центра и сосредоточенной в конечном числе радиальных трубок в атоме.

Томсон показывает, что точка" где уравновешиваются притягивающая и отталкивающая силы (^A/_a² = ^c/_a³) является центром, вокруг которого корпускула колеблется с периодом, определяемым уравнением ^2π/_T = √^ce/_ma⁴. При этом работа, производимая отталкивающей силой при удалении корпускулы из положения равновесия а в бесконечность W = ^ce/_2a². Таким образом, W пропорционально ¹/_T, т. е. v, и оказывается равным

Полагая π√Cem = h, получаем соотношение Планка. Исходя из своей модели, Томсон объясняет фотоэффект и возникновение рентгеновских лучей под действием удара катодных частиц. При этом он получает соотношение

где υ - скорость катодной частицы до удара, v - частота возникающего при ударе рентгеновского излучения. Вычисления Томсона показывают далее, что полная энергия рентгеновского излучения пропорциональна четвертой степени скорости катодных лучей, возбуждающих это излучение;

Томсоновский атом послужил также основой для теории происхождения спектральных серий, высказанной Конвеем в статье "Электромагнитная гипотеза о происхождении спектральных серий", опубликованной в том же, "боровском" томе "Philosophical Magazin". Конвей делает предположение, что томсоновский атом вращается с постоянной угловой скоростью, причем оказывается, что отдельные электроны в атоме описывают круговые орбиты с постоянным угловым моментом ^h/_π. Предполагая, что атом способен совершать упругие колебания, Конвей показывает, что сама внутренняя узловая сфера может удерживать электроны. Орбиты таких электронов не возмущаются при излучении и дают начало спектру, частоты которого определяются бальмеровской формулой

где А определяется внешней структурой атома, В - одно и то же для всех атомов и μ зависит от природы условий на поверхности для упругих волн.

Стационарные орбиты электрона определяются условием равновесия магнитных сил, обусловленных вращением заряженной сферы и притягательных электрических сил. Для таких орбит угловой момент оказывается постоянным и равным (в пределах экспериментальных ошибок) ^h/_π.

Конвей обращает внимание на связь его теории, столь отличной от теории Бора, с этой теорией. Хотя у Бора постоянный угловой момент равен ^h/_2π, но частота излучения в теории Бора равна половине угловой частоты вращения в стационарном состоянии. Угловая скорость обращения электрона по устойчивой орбите, по Конвею, выражается формулой

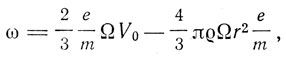
где Ω - угловая скорость вращения атома, - объемная плотность заряда атома (положительного), VQ - потенциал атома в его центре. Если атом колеблется таким же образом, как сферический объем газа при постоянном давлении, то узловыми поверхностями будут сферы радиусов, определяемых уравнением

где k, в свою очередь, определяется уравнением ka = nπ, где а - радиус сферы, n - целое число. Только самая внутренняя узловая сфера способна удерживать электрон на постоянной орбите, которая не возмущается излучением, радиус этой орбиты r = ^1,4303/_nа. Отсюда частота спектральных серий определяется формулой

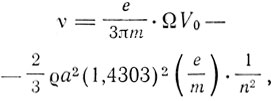
т. е. формулой Бальмера типа в v = A - ^B/_n². Конвей пытается также построить модель атомов, излучающих побочные и главную серии. Не останавливаясь на этих соображениях Конвея, рассмотрим результаты, получаемые из формулы Бальмера в интерпретации Конвея.

Угловой момент электрона в теории Конвея выражается формулой

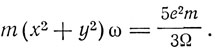
Постоянная Ридберга в теории Конвея равна

²/₃Ωa²(1,4303)²(^e/_m) = B.

Плотность заряда в томсоновской сфере определяется равенством

e = ⁴/₃πа³.

Угловой момент Конвей полагает равным ^h/_π. Подставив в вышенаписанные формулы значения

мы получим из формул Конвея значения h = 6,8*10^-27. Механизм излучения, по Конвею, описывается таким образом: электрон, имеющий частоту v, обладает кинетической энергией hv. Если он в этот момент находится на узловой сфере и вынуждается чисто радиационными силами покинуть эту сферу, то магнитная сила и, следовательно, v остаются постоянными. Однако благодаря излучению круговая орбита непрерывно уменьшается до тех пор, пока не будет излучена вся кинетическая энергия. В течение всего этого процесса излучаемая во вне радиация имеет одну и ту же частоту и ее полная величина равна hv. Остающаяся энергия будет потенциальной, и если возникает дальше какое-либо излучение, оно будет другого типа. Попытка Кон-вея спасти классическую теорию интересна тем, что в ней в какой-то мере предчувствуются идеи будущей волновой механики.

Попытки, типа попыток Томсона и Конвея примирить кванты с классическими представлениями продолжались долго. Основная идея Бора о несовместимости классической электродинамики с квантовой теорией Планка долго казалась неприемлемой. Однако теория Бора сразу обратила на себя внимание и уже в том же 1913 г. послужила основой для новых физических исследований. Теория Бора фигурирует в знаменитом исследовании Мозли по рентгеновским спектрам, опубликованным в декабрьском номере того же, 26-го тома журнала "Phil. Mag.". Оказалось, что константа v₀ в соотношении Мозли

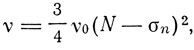
где N - порядковый номер элемента совпадает с численным значением константы Ридберга ^2π2Ω4m/_h³ вычисленной Бором, и объяснение происхождения рентгеновских линий совпадает с боровским объяснением происхождения водородных линий. "Это числовое согласие между экспериментальным значением R и вычисленным из теории, предназначенной для объяснения обычного водородного спектра, замечательно, так как длины волн, с которыми имеют дело в обоих случаях, отличаются примерно в 2000 раз". Вместе с тем Мозли отмечает, что дальнейшие эксперименты, вероятно, укажут на необходимость некоторого изменения теории. Во всяком случае, исследования Мозли по рентгеновским спектрам явились одним из первых достижений теории Бора, которое сам Мозли справедливо назвал "замечательным". Он писал: "Уже полученные результаты показывают, что подобного рода данные имеют важное значение для вопроса о внутреннем строении атома и сильно поддерживают воззрения Резерфорда и Бора".