Тепловые и механические свойства твердых тел

В этом отходе кристаллографии от минералогии и ее превращении в физическую науку решающую роль сыграли успехи физики. Развитие электронной теории привело физиков к твердому убеждению, что "механические упругие силы твердых тел в действительности есть силы электрические". Форма кристаллов, их физические и химические свойства должны определяться внутренним их строением, силами, действующими между частицами, образующими кристаллическую решетку. Так физика XX в. вернулась к идеям Гюйгенса и Гаюи.

Однако определение свойств кристаллов из строения их решеток оказалось нелегкой задачей. "Путь к решению этого вопроса был длинен. Сперва пришлось осветить с точки зрения решетки зависимость между всевозможными механическими, термическими, электрическими и оптическими свойствами кристаллов и формально свести их к силам между отдельными частицами кристаллической решетки". Так писал один из основоположников теории твердого тела Макс Борн. Как выяснилось позже, ключ к пониманию свойств твердого тела дала квантовая механика. В рассматриваемый нами период гипотеза квантов Планка была впервые применена к твердому телу Эйнштейном и позволила разрешить трудности, связанные с теорией теплоемкости, основанной на представлениях классической статистики Больцмана.

Применяя теорему о равномерном распределении энергии по степеням свободы к колебаниям атомов кристаллической решетки, получаем для внутренней энергии одного моля кристалла выражение

и значение теплоемкости

что соответствует закону, найденному экспериментально Дюлонгом и Пти еще в 1819 г. Однако к концу XIX в. выяснилось, что существуют неметаллы такие, как углерод, бор и кремний, которые в твердом состоянии имеют теплоемкость, меньшую 3R (для алмаза, например, теплоемкость порядка 1 ^кал*г/_град). Кроме того, исследования Нернста обнаружили при низких температурах зависимость теплоемкости твердых тел от температуры, а именно при приближении температуры тела к абсолютному нулю его теплоемкость также стремится к нулю.

Таким образом, классическая кинетическая теория материи оказалась не в состоянии описать полностью тепловые свойства твердого тела. На это обратил внимание в 1907 г. Эйнштейн. В статье "Теория излучения Планка и теория теплоемкости" он показывает, что применение теории Планка "ведет к видоизменению молекулярно-кинети-ческой теории, позволяющему устранить некоторые трудности, до сих пор стоящие на пути этой теории". В своей статье Эйнштейн предполагает, что закон равномерного распределения энергии по степеням свободы неприменим не только к черному излучению, но и к колебаниям молекул твердого тела. Предполагая, что все молекулы твердого тела ведут себя как планковские осцилляторы, колеблющиеся с одной и той же частотой v, он принял, что они обладают в среднем энергией осциллятора Планка, так что полная энергия одного моля

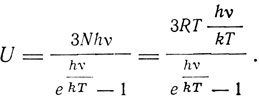
Для слабых связей осцилляторов с положением равновесия hv<<kT и U≅3RT - закон Дюлонга и Пти. Но, если hv≥kT, что имеет место для крепкой связи (алмаз) или при низких температурах, закон Дюлонга и Пти более не имеет места, что и было подтверждено качественно опытами Нернста и его сотрудников.

В количественном отношении формула Эйнштейна не вполне соответствует опыту, и Нернст и Линдеман в 1911 г. заменили ее другой, лучше согласующейся с опытом. Формула Нернста и Линдемана имеет вид

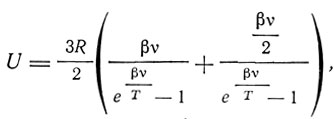
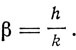
Отсюда теплоемкость

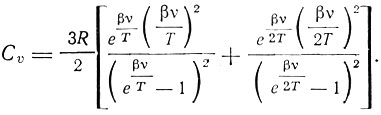
В связи с формулой Нернста и Линдемана Эйнштейн писал в работе "Элементарное рассмотрение теплового движения в твердых телах", опубликованной в том же, 1911 г.:

"Колебания атомов не являются гармоническими даже приближенно. Интервал частот атома настолько велик, что изменение энергии колебания в течение полупериода по порядку величины равно самой энергии. Значит, каждому атому следует приписывать не какую-то одну определенную частоту, а интервал частот Δv по порядку величины, равной самой частоте. Чтобы получить для удельной теплоемкости твердых тел точную формулу, надо было бы, основываясь на некоторой механической модели, провести для атома твердого тела рассмотрение, совершенно аналогичное выводу Планка для случая осциллятора с бесконечно малым затуханием. Следовало бы определить, при какой средней энергии колебания атом, обладающий электрическим зарядом, излучает в поле теплового излучения столько же энергии, сколько поглощает.

Пока я почти без успеха бился над этой программой, Нернст прислал мне корректурный оттиск работы, содержащий поразительно хорошее предварительное решение задачи. Он нашел, что формула (здесь Эйнштейн приводит вышенаписанную формулу Нернста и Линдемана) для теплоемкости, превосходно изображает температурную зависимость атомной теплоемкости. То обстоятельство, что эта формула согласуется с опытом лучше, чем моя первоначальная, в соответствии со сказанным выше легко объясняется. Ведь эту формулу можно получить, предполагая, что атом совершает квазинезатухающие синусоидальные колебания половину времени с частотой v, а другую половину времени - с частотой ^v/₂. Значительное отклонение колебаний от монохроматических отражается этим способом самым простым путем". В приведенном отрывке очень хорошо показаны искания Эйнштейном новых путей в решении проблемы теплоемкости. Эти поиски заставили его размышлять над вопросами связи оптических, тепловых и упругих свойств кристалла. Этим вопросом занимались и многие другие авторы.

В 1908-1910 гг. Э. Грюнейзен, исследуя упругие свойства металлов, пришел к выводу, что отношение коэффициента теплового расширения металла к его удельной теплоемкости не зависит от температуры. В 1911 г., опираясь на теорему Нернста, Грюнейзен показал, что коэффициент расширения должен представляться той же температурной функцией, что и удельная теплоемкость. Таким образом, упругие и тепловые свойства оказались связанными с собственными частотами колебаний атомов в решетке. Эйнштейн (1911) в работе "Связь между упругими свойствами и атомной теплоемкостью в твердых телах с одноатомными молекулами" и несколько ранее Сезерленд (1910) и Э. Маделунг (1909) установили связь между сжимаемостью кристалла и частотами колебаний его атомов.

Э. Грюнейзен пытался вывести общее соотношение, связывающее упругие и тепловые свойства кристалла - его уравнения состояния. Он рассматривал одноатомное твердое тело и, следуя идеям Ми, высказанным последним в 1903 г., предположил, что атомы твердого тела находятся в равновесии под действием притягательных и отталкивательных сил. Ми и, следуя ему, Грюнейзен полагали, что силы сцепления аналогичны ван-дер-ваальсовым силам и потенциальная энергия, соответствующая этим силам, имеет вид

Отталкивательные силы меняются с расстоянием значительно быстрее притягательных, и соответствующая им доля потенциальной энергии равна

При абсолютном нуле твердое тело по Грюнейзену представляет статическую систему, в которой атомы находятся в определенных положениях равновесия, в которых действия притягательных и отталкивательных сил уравновешиваются. При нагревании кристалла происходит смещение атомов из их положения равновесия и в связи с этим возбуждаются их тепловые колебания. Грюнейзен считает атомы гармоническими осцилляторами, в которых кинетическая энергия в среднем равняется потенциальной и полная энергия колебаний выражается интегралом ∫^T₀C_vdT. Применяя теорему вириала Клаузиуса, Грюнейзен находит уравнение состояния, которое мы здесь выписывать не будем, так как ни Грюнейзену, ни его предшественнику Ми не удалось получить уравнения состояния, удовлетворительно согласующегося с опытом. Однако Грюнейзену удалось получить формулу, связывающую частоту колебаний атомов с упругими константами кристалла. Формула Грюнейзена

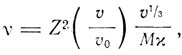
где Z - число, зависящее от расположения атомов в теле, М - атомный вес, א - коэффициент сжимаемости, υ - атомный объем, υ₀ - атомный объем при абсолютном нуле. Эйнштейн в том же, 1911 г., что и Грюнейзен, но несколько раньше (Грюнейзен ссылается на работу Эйнштейна), исходя из представления, что твердое тело имеет плотную кубическую упаковку атомов, вычислил коэффициент Z2; формула Эйнштейна имеет вид

v = 2,77*10⁷M^-1/₃-1/₆א^-1.₂.

Здесь вместо атомного объема v фигурирует плотность . И у Грюнейзена, и у Эйнштейна кристалл обладает только одной частотой упругих колебаний.

Вычисление теплоемкости твердого тела при учете наличия спектра упругих колебаний - акустический спектр - было проведено в 1912 г. П. Дебаем в работе "К теории удельных теплоемкостей" и в том же и последующем году М. Борном и Т. Карманом в статьях "О колебаниях пространственной решетки" (1912), "К теории удельной теплоемкости" (1913) и "О теории распределения собственных колебаний точечной решетки". Как видно из названий статей Борна и Кармана, в основе их теории лежала модель кристаллической решетки, частицы которой, расположенные в ее узлах, были способны совершать гармонические колебания. Тепловая энергия твердого тела - это энергия этих колебаний, и Борн и Карман подсчитывали ее с помощью приближенных методов. Результат их вычислений совпадал с результатом, полученным Дебаем, работу которого мы рассмотрим подробнее в виду ее важного исторического значения.

Дебай начинает свою статью ссылкой на исследования Нернста, показавшие неприменимость теоремы равномерного распределения энергии к теории теплоемкости. Указав далее на результаты Эйнштейна и формулу Нернста-Линдемана, он отмечает, что предположение о единственности частоты колебаний, принятое Эйнштейном в работе 1907 г., "не может быть оправдано, как предположил уже Эйнштейн" (Дебай ссылается на статью Эйнштейна 1911 г.). "Окружение вибрирующего атома,- говорит Дебай,- оказывает на него такое сильное влияние, что его движение лишь весьма отдаленно напоминает простое гармоническое движение". В результате прямое применение формулы Планка становится сомнительным. Если же представить движение атома с помощью разложения Фурье, то детальное проведение вычисления энергии и теплоемкости становится трудной задачей. Дебай предлагает метод расчета, аналогичный доказательству Джинса для рэлеевского закона излучения. Твердое тело, состоящее из N атомов, трактуется как система с 3N степенями свободы, совершающая 3N различных колебаний. Дебай рассматривает в своих вычислениях твердое тело как непрерывную среду и исходит из уравнений теории упругости. "Прерывную структуру тела,- пишет Дебай,- мы будем принимать в расчет только постольку, поскольку она приводит к следствию, что спектр состоит в целом только из 3N, а не бесконечно многих спектральных линий. В соответствии с этим, спектр, вычисленный из уравнений упругости, будет обрезаться до 3N спектральных линий". Результаты своих расчетов Дебай сводит в первой части работы. Вначале он приводит выражение для числа колебаний тела объема V, с частотами ниже некоторой частоты v:

здесь F - функция упругих констант; сжимаемости א, отношения Пуассона σ и плотности :

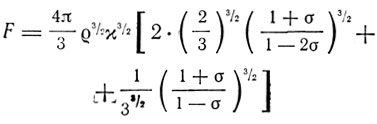
(2)

Максимальная частота колебаний v_m определяется выражением

Плотность спектральных линий дается формулой

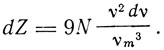
(4)

Каждое из колебаний в соответствии с формулой Планка обладает энергией

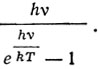
(5)

Полная энергия тела

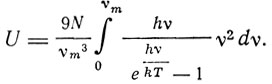
(6)

Дебай вводит далее константу, названную им характеристической температурой тела,

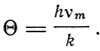
(7)

Введя новую переменную

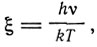
(8)

получим

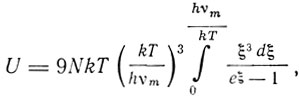
или

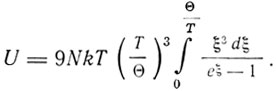
(9)

Отсюда получается выражение для теплоемкости

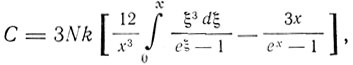
(10)

где

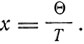
Дебай формулирует полученные им результаты в следующих девяти пунктах:

1. "Для твердого тела не существует единственной частоты колебаний атомов, как это предполагал первоначально Эйнштейн при подсчете удельной теплоемкости. Твердое тело может быть характеризовано лишь полным спектром собственных частот.
2. Спектр обладает конечным числом линий (равным трехкратному числу атомов). Линии низких частот - обычные акустические колебания.
3. Спектр может быть характеризован плотностью спектральных линий на интервале частот dv. Мы нашли, что число колебаний, приходящихся на этот интервал, пропорционально v²dv. Фактор пропорциональности вычисляется из упругих констант вещества.
4. При использовании (3), формулы для полной энергии и удельной теплоемкости могут быть получены, если каждой степени свободы приписать энергию
   
   
   соответственно квантовой теории.
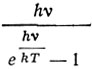
5. Эта процедура приводит к выражению для удельной теплоемкости, которое зависит только от отношения ^θ/_Т, где θ - температура, характерная для данного тела. Удельная теплоемкость одноатомного твердого тела будет, таким образом, универсальной функцией отношения ^θ/_Т.
6. Для низких температур из окончательной формулы (или также непосредственно из (3)) можно вывести, что удельная теплоемкость пропорциональна Т³ для всех веществ. Тогда величина энергии пропорциональна Т⁴, точно так же, как для излучения по закону Стефана-Больцмана, справедливому для всех температур. Этот предельный закон особенно просто демонстрирует отличие нашей формулы от формулы Эйнштейна или формулы Нернста-Линдемана. Согласно двум последним формулам удельная теплоемкость при низких температурах стремится к нулю по экспоненте.
7. Сравнение нашей формулы с наблюдениями над алмазом, алюминием, медью, серебром и свинцом показывает очень хорошее согласие теории с экспериментом.
8. В Определенном смысле формула Нернста и Линдемана является приближением к нашей формуле. Это объясняет, почему в прежних исследованиях последняя формула показывала такое хорошее согласие с экспериментом.
9. Характеристическая температура θ может быть вычислена из упругих констант, и результаты вычисления являются хорошими. Помимо числового множителя, наша формула отличается от формулы, данной ранее Эйнштейном, поскольку она содержит не только сжимаемость, но также и отношение Пуассона". Итак, теоретический анализ свойств твердого тела, проделанный Эйнштейном, Дебаем, Борном и Карманом, выявил важную роль частот атомных колебаний, с которыми связаны упругие и тепловые свойства кристаллов. Экспериментальная проверка теории, прежде всего, состояла в определениях этих частот. В своем докладе в Геттингене в 1913 г. о кинетической теории твердого тела В. Нернст указывал, что из трех величин, характеризующих состояние твердого тела, а именно его массы, атомного объема и атомной частоты, наиболее трудно поддаются экспериментальному определению последние и, однако, уже наметились разнообразные методы их определения.

В числе таких методов Нернст указал следующие:

1. Метод удельных теплоемкостей, который позволяет по теоретическим формулам типа дебаевской определить атомные частоты наиболее надежным способом.

2. Метод определения точки плавления. В 1910 г. и более подробно в своей диссертации 1911 г. Ф. А. Линдеман, рассматривая молекулярную теорию твердого тела, предположил, что точка плавления определяется нарастанием амплитуды тепловых колебаний, которые становятся соизмеримыми с межатомными расстояниями. В результате взаимные соударения колеблющихся атомов разрушают межатомные связи и тем самым структуру кристалла. Обозначив через r₀ орбиту кругового движения атома при точке плавления T_s, так что скорость колеблющейся частицы u = 2πr₀v,мы получим для средней энергии атома

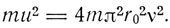
По формуле Планка-Эйнштейна эта средняя энергия

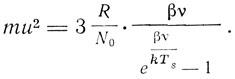
Но при точке плавления β_v<< kT_s справедлив закон Дюлонга и Пти и, следовательно,

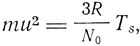
т. е.

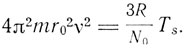
Таким образом, частота атомных колебании пропорциональна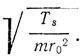

Так как, в свою очередь, среднее расстояние между атомами пропорционально корню кубическому из атомного объема, то Линдеман получает следующую формулу:

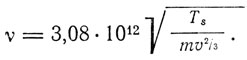
3. Метод упругих констант. Как мы уже говорили, связь упругих констант с атомными частотами исследовалась

Маделунгом, Эйнштейном, Грюнейзеном, Линдеманом. Приближенная формула такой зависимости

v = 3,0*10⁷m^-1/₃-1/₆א^-1/₂,

где m - атомный вес, - плотность, א - сжимаемость. Значительно более точные результаты дает теория Дебая-Борна-Кармана, где предельная частота связана с средней скоростью звуковых волн ст. Расчеты Борна и Кармана дали следующее выражение:

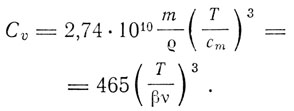
Средняя скорость звука определяется через продольную и поперечную скорость уравнением

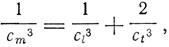
где c_l - скорость продольных, c_t - скорость поперечных звуковых волн.

4. Метод теплового расширения. По закону Грюнейзена, в одноатомных телах коэффициент теплового расширения и теплоемкость пропорциональны друг другу. Поэтому, по Грюнейзену, имеет место соотношение

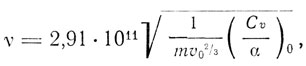
где v₀ - атомный объем при абсолютном нуле, α = ¹/_v*^dv/_dT - коэффициент теплового расширения. Уравнение Грюнейзена хорошо подтверждается опытом.

5. Оптический метод. Для кристаллов типа каменной соли в узлах решетки находятся ионы, колебания которых сопровождаются испусканием электромагнитных волн инфракрасных частот. Исследуя поглощение или отражательную способность таких кристаллов, находят, что вблизи собственных частот атомов тело обладает аномально высокой отражательной способностью. Если излучение сложного спектрального состава неоднократно отражается от такого тела, то, в конце концов, в отраженном луче остаются только те волны, для которых имеет место это аномально высокое отражение. Этот метод остаточных лучей был разработан Г. Рубенсом.

6. Наконец, Нернст упоминает еще об одном методе - методе определения электропроводности при низких температурах. Как известно Каммерлинг-Оннес открыл аномально высокое падение сопротивления в области низких температур (сверхпроводимость). При низких температурах также убывает атомная теплоемкость и коэффициент теплового расширения. В 1911 г. Каммерлинг-Оннес и Нернст установили независимо друг от друга, что убывание термического коэффициента происходит при тем более низкой температуре, чем ниже атомная частота соответствующего металла. Таким путем можно оценить атомную частоту у какого-либо металла, поместив его между металлами, атомные частоты которых уже известны. С другой стороны, Грюнейзен в 1913 г. установил, что отношение сопротивления к абсолютной температуре возрастает в области низких температур приблизительно пропорционально атомной теплоемкости.

Эйкен в своем курсе химической физики сопоставляет значения величины

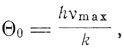
определенные различными методами, в частности по формуле Эйнштейна: v = 3,0*10⁷m^-1/₃-1/₆א^-1/₂, Дебая: 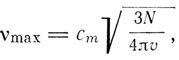Грюнейзена: 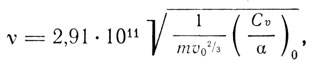Линдемана: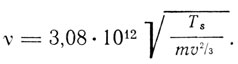

Обсуждая полученные результаты, Эйкен резюмирует, что совпадение результатов в общем и целом вполне удовлетворительно, и это доказывает, что атомные частоты известны с точностью до 10%, и что теория Дебая дает правильные значения для теплоемкости.

Вопросы квантовой теории вещества рассматривались в апреле 1913 г. в геттингенском докладе Дебая "Уравнение состояния и квантовая гипотеза". Добавление к докладу содержит теорию теплопроводности. Во вступительных замечаниях к своему докладу Дебай указывает ка несостоятельность классической статистики в области низких температур и на универсальную значимость планковского выражения для средней энергии осциллятора, позволяющего дать точное решение не только проблемы черного излучения, но и теории теплоемкости твердого тела. Вместе с тем он обращает внимание на то, что опытом исследуется только производная внутренней энергии но температуре и тем самым остается открытым вопрос о существовании в выражении внутренней энергии постоянного члена, не обращающегося в нуль при абсолютном нуле. Этот постоянный член есть так называемая "нулевая энергия", значение которой было подчеркнуто Эйнштейном в 1911 г. Дебай указывает, что открытие рентгеноструктурного анализа Фридрихом, Книппингом и Лауэ позволяет надеяться, что в недалеком будущем можно экспериментально сделать выбор между выражениями внутренней энергии твердого тела. Далее Дебай ставит общую задачу установления уравнения состояния на основе квантовой теории. Он указывает на работы Грюнейзена в этом направлении, обобщенные в его докладе "Молекулярная теория твердого тела" на втором Сольвеевском конгрессе 1913 г. Дебай подходит к проблеме уравнения состояния твердого тела, исходя из представления об ангармоническом осцилляторе. Именно представление о молекуле твердого тела как ангармоническом осцилляторе позволяет объяснить факт увеличения объема тела с температурой. Полагая потенциальную энергию осциллятора записанной в виде степенного ряда по степеням х, где х смещение частицы из положения равновесия х = 0, имеем

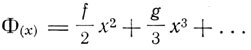
Таким образом, во втором приближении потенциальная энергия несимметрична относительно положения равновесия х = 0. Уравнение движения частицы

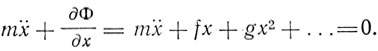
Решение этого уравнения в первом приближении имеет вид

где 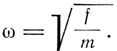Чтобы найти второе приближение, подставляем это значение в член gx² и тогда получим

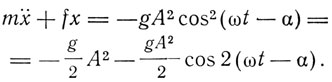
Откуда во втором приближении

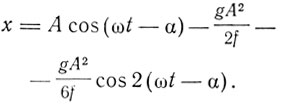
Для теории важно значение среднего смещения

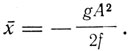
Квадрат амплитуды можно заменить из выражения энергии осциллятора

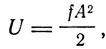
и тогда

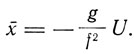
Следовательно, с возрастанием энергии колебания центр колебаний смещается, причем это смещение пропорционально энергии. Это соответствует теореме Грюнейзена о пропорциональности коэффициента расширения удельной теплоемкости. Таким образом, термическое поведение тела описывается моделью ангармонического осциллятора, но формула Планка применима только к гармоническим колебаниям. Эту трудность Дебай обходит с помощью приближенного метода, рассматривая колебания вокруг нового центра 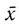и применяя к этим колебаниям выводы Планка. При этом частота колебаний оказывается зависящей от смещения 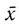(в первом приближении v₁ = v₀(1 + ^g/_f)*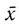. Применяя выводы, полученные для ангармонического осциллятора к твердому телу, Дебай получает следующее приближенное выражение для запаса энергии твердого тела U и для его уравнения состояния:

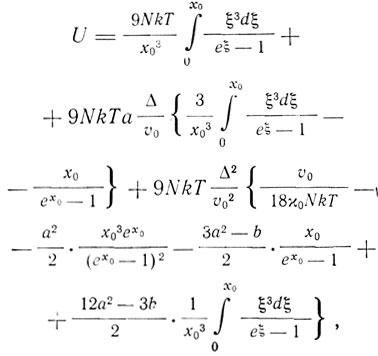
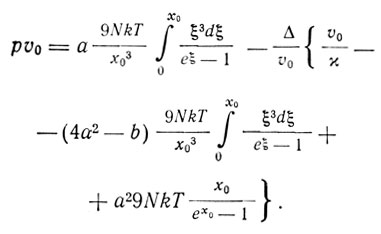
Здесь Δ - растяжение первоначального объема υ₀, א₀ - коэффициент сжимаемости при температуре T = 0, א₀ = ^Θ₀/_T; а и b - члены разложения величины Θ₁ = ^hv1_max/_k.

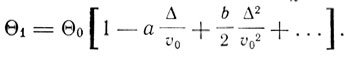
Если а = b = 0, то для U получается

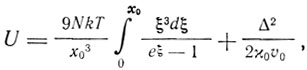
из которого вытекает закон температурной зависимости "T⁴" Дебая. Уравнение состояния принимает в этом случае вид

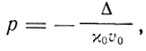
т. е. никакой зависимости р от температуры нет (растяжение Δ предполагается вызванным внешними силами). Дебай получает из уравнения состояния при р = 0 (атмосферное давление) в первом приближении закон Грюнейзена

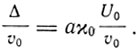
Что касается температурной зависимости коэффициента расширения, то она в теории Дебая определяется законом "T³".

Наиболее замечательным в теории Дебая является применение идеи квантования к ангармоническому осциллятору. Вместе с тем асимметричный характер потенциальной функции в дальнейшем был усвоен в теории твердого тела Борном, Маделунгом и другими авторами, разработавшими теорию твердого тела.

Как было уже сказано, доклад Дебая был одним из геттингенских докладов по кинетической теории материи и электричества, читавшихся в Геттингене в апреле 1913 г. Эти доклады были опубликованы в 1914 г. под общим заглавием "Доклады о кинетической теории материи и электричества" с предисловием известного математика Д. Гильферта^*. Одной из тем докладов была квантовая теория газов, которой был посвящен доклад Планка, рассмотренный нами в седьмой главе. Кинетическая теория твердого тела была предметом доклада Нернста, о котором мы уже упоминали выше.

^* (Мы их называли выше (см. главу шестую) геттингенскими докладами.)

Из доклада Нернста ясно видны успехи и трудности теории твердого тела. Еще неясна природа частиц, образующих кристаллическую решетку, не найден закон межатомных сил, теория Дебая учитывает квантовые свойства искусственным приемом обрезания частот. Нернст хочет улучшить теорию Дебая учетом атомной структуры, но сам признает, что его вывод не является строго обоснованным. Вместе с тем уже поведение тел при низких температурах нашло отражение в теории Дебая, хорошо согласующейся с опытом в этой области температур. Не случайно, что А. Зоммерфельд, также в геттингенском докладе, посвященном кинетической теории газов, пытается построить квантовую теорию газа по образцу теории твердого тела Дебая.

Доклад Зоммерфельда носил название "Проблемы длины свободного пробега". Первый раздел доклада как раз посвящен квантовой теории одноатомного газа. Вопрос о применении квантовой теории к идеальному одноатомному газу был поставлен в порядок дня. Его обсуждали в своих докладах и Планк, и Нернст. Применение квантовой теории к газу позволило Саккуру и Нернсту определить константу энтропии. Зоммерфельд примыкает к Планку и Нернсту в их попытках построить квантовую модель газа. Здесь он опирается на метод Рэлея-Джинса в теории излучения, примененный Дебаем в теории теплоемкости твердого тела. Газ мыслится заключенным в кубический сосуд с ребром l, так что объем газа υ = l³. Число молекул газа в этом объеме N, число степеней свободы всей системы 3N. Это число равно числу собственных колебаний системы. "Длина волны", соответствующая отдельному собственному колебанию частоты υ, λ = ^с/_ν. Далее, через N' обозначается число собственных колебаний, длина волны которых лежит вне λ, и dN' - число собственных колебаний, длина волны которых лежит в области λ, λ+dλ. Газ рассматривается как континуум, каждое собственное колебание которого характеризуется тремя числами а, Ь, с, равными трем ребрам куба, заключенного между узловыми плоскостями. Основное колебание имеет длину волны 2l и

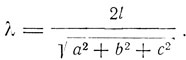
Тогда

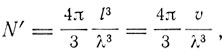
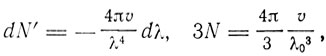
где λ₀ - граница акустического спектра, определяемая тем, что соответствующее максимальное число N' равно числу степеней свободы 3N. Все эти подсчеты совпадают с соответствующими величинами в теории Дебая, за исключением того, что здесь используется длина волны λ, а не частота v, как в теории Дебая. Для скорости звука в этом континууме имеем формулу:

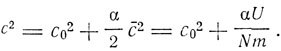
Здесь c₀ - часть, обусловленная взаимным расположением атомов (потенциальная энергия), U - кинетическая энергия молекул во всем объеме v. Для твердого тела α<<c₀ и c = c₀. Для газа c₀ мало и α = ¹⁰/₉*²/₃^C_p/_Cv, так что получается обычная формула для скорости звука в газе:

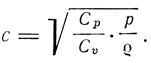
Далее Зоммерфельд в соответствии с методом Планка вычисляет функцию распределения f элементов энергии hv по резонаторам. Тогда энтропия газа

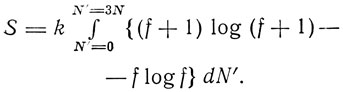
Для наиболее вероятного распределения, соответствующего стационарному состоянию газа, Зоммерфельд находит

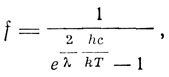
и энтропия

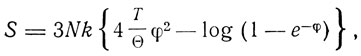
где

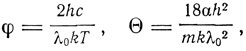
и граничная длина волны определяется равенством

Далее доказывается, что

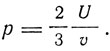
"Тем самым,- пишет Зоммерфельд,- из метода собственных колебаний мы находим характерную связь между давлением и плотностью энергии, которая является основной в кинетической теории газов, где она записывается в виде соотношений

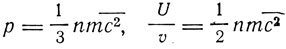
(n - число молекул в единице объема, с^-2 - средний квадрат скорости). Поэтому в качестве первого результата мы имеем: метод собственных колебаний эквивалентен кинетическому методу. Именно он дает то же самое соотношение между давлением и энергией, которое вытекает из кинетического представления этих величин (давление - импульс поступательного движения, энергия - кинетическая энергия)".

Далее для высоких температур получается (Т>>θ)

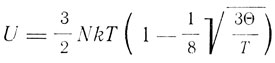
и уравнение состояния

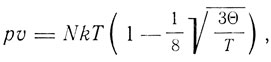
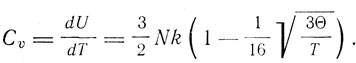
Отсюда в первом приближении

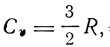
где R = Nk. Таким образом, "метод собственных колебаний дает автоматически, до известной степени без нашего участия, правильное выражение ³/₂R для теплоемкости, совпадающее со значением, даваемым законом Дюлонга и Пти для твердого тела". Для аддитивной константы энтропии этот метод дает то же значение, какое дает квантовая теория

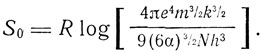
Для низких температур

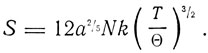
Таким образом, и для газов энтропия при абсолютном нуле обращается в нуль - в соответствии с новой формулировкой тепловой теоремы Нернста, если абсолютный нуль может быть достигнут при постоянном θ без конденсации.

Значение, данное Саккуром для постоянной энтропии,

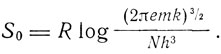
Оно отличается от данного выше на

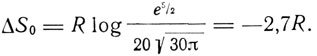
Таким образом, формула Зоммефельда не дает числового согласия с формулой Саккура. Однако Зоммерфельд указывает, что его формула зависит от известных величин k, h, m совершенно так же, как формула Саккура, и, следовательно, дает такую же универсальную зависимость между элементарной областью вероятности g и h³, какую постулирует Планк в своем докладе.

Зоммерфельд рассматривает далее уточнения своей теории, если принять во внимание нулевую энергию. Оказывается, что при этом различии в константах энтропии разность между его формулой и формулой Саккура ΔS₀ не уменьшается, а увеличивается. Другой способ улучшения теории Зоммерфельд видит в том, чтобы ввести в расчет длину свободного пробега или среднее время между соударениями. Если сравнить путь молекул с колебательным процессом, чтобы иметь возможность применить правило квантования Планка, то это среднее время должно играть приблизительно такую же роль, как половина периода. Другой метод введения квантовых представлений в теорию газов опирается на соотношение Зоммерфельда между величиной передаваемой энергии и временем ее передачи. И этот способ взедения квантов будет также учитывать длину свободного пробега. Однако мы не будем больше останавливаться на попытках построения квантовой теории газов: они не привели к успеху и не решили всех проблем, в частности проблемы вырождения газа. Нужна была новая статистика, которая и была создана через десять лет после публикации доклада Зоммерфельда. Сам доклад представлял любопытную попытку применить методы, приведшие к успеху в теории твердого тела, к газам. Именно поэтому он и был рассмотрен нами в главе о физике твердого тела.