Электропроводность металлов

Переходим теперь к рассмотрению электрических свойств твердого тела. Из этой области наибольшее развитие получила теория электропроводности металлов.

Уже в 1898 г. Э. Рикке предположил, что молекулы металла частично диссоциированы и в пространстве между молекулами имеются положительно и отрицательно заряженные частички. Поведение этих частиц определяется законами кинетической теории газов, однако плотность их настолько мала, что в расчет принимаются только их столкновения с молекулами металла, но не столкновения их между собой. Ток представляет упорядоченный поток этих частиц: положительно заряженных по направлению поля, отрицательно заряженных против поля. Существованием таких частиц Рикке объяснял и контактную разность потенциалов.

Рикке пытался выяснить, происходит ли перенос вещества в металлах током, обусловленным движением этих частиц. С этой целью он пропускал довольно сильный ток (около 10 ампер) в течение нескольких лет через цепь, составленную из кусков золота и серебра, плотно прилегающих друг к другу. Он не обнаружил никакого проникновения атомов золота в серебро и наоборот. Таким образом, носители электрического тока в металле являются не ионами, как в электролитах, а частицами, не связанными с массами обычных атомов.

В 1900 г. теорию электропроводности металлов развил Пауль Друде. Друде принимает, что электропроводность металлов обусловлена наличием свободных электронов. Однако наряду с отрицательными электронами он допускает и наличие положительных электронов, причем ток создается совместным направленным движением электронов обоего рода в противоположных направлениях. Друде применяет к электронам выводы классической теории газов (электронный газ) и принимает, что вследствие взаимных столкновений электронов между собой они в среднем получают одинаковую кинетическую энергию, пропорциональную абсолютной температуре

где α = ³/₂^R/_N.

На это движение под действием электрического поля напряженностью Е накладывается упорядоченное движение со скоростью v, в результате чего создается ток плотностью j = nev, при этом v = ¹/₂ft, где f - ускорение электрона, равное f = ^Ee/_m, a t - время пробега электрона от столкновения до столкновения, равное t = ^λ/_u, где λ - длина свободного пробега. Подставляя для m значение m = ^2αT/_u², получаем для плотности тока

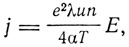
т. е. закон Ома: j = kE, где коэффициент электропроводности

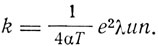
Отсюда Друде находит соотношение между теплопроводностью К и электропроводностью k:

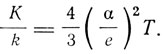
Таким образом, при постоянной температуре теплопроводность и электропроводность металла пропорциональны друг другу. Этот закон был установлен экспериментально в 1853 г. Г. Видеманом и Р. Францем и носит название закона Видемана-Франца. Теория Друде объяснила этот закон теоретически. В том же, 1900 г., когда Друде выступил с своей теорией электропроводности, Д. Д. Томсон на Международном конгрессе физиков в Париже излагал свою теорию этого предмета. Собственно говоря, Томсон развил две теории: одну почти целиком совпадающую с теорией Друде, теорию электронного газа, и другую, которую можно назвать поляризационной. Отличие первой теории Томсона от теории Друде заключается, прежде всего, в том, что Томсон рассматривает только один род носителей - отрицательно заряженные корпускулы, т. е. электроны. Другое отличие состоит в том, что в формулы Томсона входит коэффициент р. Этот коэффициент учитывает остаточное влияние электрического поля на корпускулу в момент ее столкновения. Поэтому средняя скорость корпускулы, приобретаемая под действием электрического поля, будет не ¹/₂^Ee/_mt, как у Друде, а ¹/₂β^Xe/_mt, где X - обозначение Томсона для напряженности электрического поля. Коэффициент β у Томсона несколько больше 1. Однако для практических расчетов Томсон полагает его равным 1 и, таким образом, например, получает такую же форму закона Видемана-Франца, как и у Друде.

С помощью представления о свободных электронах Томсон получает объяснение термоэлектрических явлений (явления Пельтье и Томсона), а также явления Холла. Но в последнем случае встречается одно затруднение: явление Холла в различных веществах имеет разный знак. Друде обходил это затруднение, предполагая существование двух родов носителей тока: отрицательных и положительных. В зависимости от природы вещества в нем может преобладать либо ток отрицательного, либо ток положительного электричества (прообраз современной электронной и "дырочной" проводимости). Однако Томсон, принимая за носителей тока только отрицательно заряженные корпускулы, отклоняет эту теорию. Причину различия эффекта Холла он усматривает в неодинаковости действия магнитного поля на корпускулы во время их свободного движения и во время их столкновения. Последнее действие в зависимости от природы молекул может совпадать с действием на корпускулу при свободном движении, а может быть и прямо противоположным. Вместе с тем Томсон указывает, что применять образы кинетической теории газов к металлам следует с большой осторожностью; строение куска металла резко отличается от строения газов. "Кусок металла, по-видимому, представляет собой агрегат большого числа маленьких кристаллов",- пишет Томсон.

Томсон останавливается также и на теории теплового излучения электронами, движущимися в металле. Эта теория была предложена Лоренцем и о ней говорилось в шестой главе.

По второй теории Томсона проводимость обусловлена переходом корпускулы вдоль цепочки поляризованных атомов от одного атома к другому. По этой теории отношение теплопроводности к электропроводности равно

где υ - абсолютная температура, d - длина оси поляризованного атома (диполя), b - расстояние между диполями. Для плотно расположенных диполей d∼b и это отношение равно ³/₂^α2υ/_e², в то время как по первой теории оно равно ⁴/₃^α2υ/_e², т. е. отношение обоих величин равно ⁹/₈. Томсон считает, что этот результат не хуже прежнего. Такой же результат получается и для лучистой энергии. Поэтому Томсон полагает, что при современном состоянии наших знаний мы не можем сказать, какая из этих теорий лучше согласуется с фактами".

В 1903 г. Г. А. Лоренц опубликовал статью "Об испускании и поглощении металлами тепловых лучей больших длин волн", на результаты которой и ссылается Д. Д. Томсон в своей теории проводимости в 1906 г. в книге "Корпускулярная теория материи". Выше мы приводили этот результат, который является не чем иным, как законом Рэлея-Джинса. В этой статье Лоренц исходит из теории проводимости Рикке-Друде и опытов Гагена и Рубенса 1903 г. по отражательной способности металлов для лучей длин волн более 8μ. Из этих опытов следует, что поведение металлов при отражении таких волн определяется только их проводимостью. Лоренц кратко излагает суть теории Друде и приводит его выражение для электропроводности, на которое он и опирается в последующих расчетах излучательной и поглощательной способности металлов. В 1905 г. Лоренц развивает дальше кинетическую теорию электропроводности, предполагая, что распределение тепловых скоростей электронов подчиняется закону Максвелла. Он получает при этом выражение для коэффициента электропроводности в виде

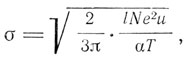
где N - число электронов в единице объема, μ - скорость теплового движения, l - длина свободного пробега, тогда как эта же величина по Друде будет

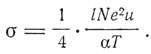
Закон Видемана-Франца в теории Лоренца имеет вид

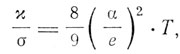
тогда как у Друде

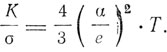
Лоренц так же, как и Томсон, прилагает свою теорию к термоэлектрическим явлениям, объясняя и явление Пельтье, и явление Томсона.

Камнем преткновения для теории свободных электронов в металле было явление Холла, которое, как кажется, говорит в пользу гипотезы двух родов носителей тока. 17 апреля 1906 г. Лоренц прочитал лекцию "О положительных и отрицательных электронах" в Американском философском обществе в Филадельфии, основанном Б. Франклином. Разбирая гипотезу двух родов электричества, Лоренц приходит к выводу, что она противоречит второму закону термодинамики и, следовательно, электрический ток в металле обусловлен движением частиц одного рода, отрицательно заряженных электронов. Свою лекцию Лоренц заканчивает следующими словами: "Поскольку эффект Холла на первый взгляд кажется очень сильно благоприятствующим теории двух флюидов, мы должны исследовать, не может ли он быть объяснен движением только отрицательных электронов. Если мы преуспеем в этом, проникнув возможно глубже в механизм явления... то мы после всего придем к системе объяснения, значительно напоминающей франклинову унитарную теорию электричества".

Однако теория свободных электронов наталкивалась на серьезные трудности. Она приводила к закону Рэлея-Джинса для теплового излучения электромагнитных волн, возникающих при столкновениях электричеств, не объясняла отсутствия вклада электронов в теплоемкость металла. Наконец, улучшение теории Друде Лоренцем привело к ухудшению соответствия теории и опыта: константа Видемана-Франца в теории Лоренца хуже соответствует опыту, чем константа Друде. К этим затруднениям прибавилось -еще одно.

Х. Каммерлинг-Оннес в своей лаборатории

10 июля 1908 г. в Лейденской лаборатории низких температур Хейке Каммерлинг-Оннес, завершая длительный период поисков методов сжижения "постоянных" газов, обратил в жидкость гелий, последний оставшийся после сжижения водорода "постоянный газ". Трудность обращения гелия в жидкость состояла в том, что у гелия была очень низкая температура инверсии. Если для водорода эта температура -80° С, то для гелия она составляла -240°. Между тем, для того чтобы использовать эффект Джоуля-Томсона для охлаждения газа, он должен расширяться при температуре ниже точки инверсии. Поэтому гелий должен быть предварительно охлажден жидким водородом и потом уже расширяться через дроссельный вентиль.

Гелиевый ожижитель Каммерлинг-Оннеса показан на рисунке. Жидкий водород непрерывно переливается сифоном из градуированного сосуда Ga. Гелий подавался компрессором под давлением 100 атмосфер и последовательно

1. проходил через водяной охладитель и масляный отстойник Са;
2. проходил через трубки Db и Da, где он охлаждается возвратными потоками водорода и гелия;
3. освобождался от последних остатков воздуха в трубке Сb, заполненной древесным углем, охлажденным жидким воздухом;
4. проходил через трубки В₃, В₂ и В, охлаждавшиеся соответственно жидким воздухом, парами водорода и жидким водородом;
5. проходил через четырехходовую спираль А к дроссельному вентилю М₁М₂. Образовавшийся жидкий гелий собирался в дьюаровом сосуде Е_а, а газообразный возвращался обратно в компрессор.

N₁, N₂, N₃, N₄ - водородные термометры,

Th₁, Th₂, Th₃, ThA₄, Th₅ - гелиевые термометры.

Каммерлинг-Оннес получил с этим аппаратом при первом опыте 60 кубических сантиметров жидкого гелия.

В 1911 г., продолжая опыты с жидким гелием, Каммерлинг-Оннес опускал в ванну с жидким гелием ртутный проводничок. При температуре 4° К сопротивление проводничка составляло 0,04 ом. При 3°К сопротивление падало скачком до 3*10^-8 ом. В дальнейшем выяснилось, что сопротивление при температуре ниже точки перехода не превышает 10^-11 начального сопротивления. Каммерлинг-Оннес пришел к выводу, что "ртуть переходит в новое состояние, которое вследствие его необычных электрических свойств может быть названо сверхпроводящим состоянием" (1913).

Явление сверхпроводимости поставило теорию электронного газа перед чрезвычайными трудностями. Вин в 1913 г. пришел к выводу, что "электронная теория металла должна быть построена на существенно новой основе". Он предположил, что скорость свободных электронов совершенно не зависит от температуры. При правильной кристаллической решетке ее проводимость должна быть бесконечной, что соответствует опытам Каммерлинг-Оннеса. Тепловые колебания атомов нарушают эту правильность и сопротивление становится конечным. Столкновение электронов с атомами вещества производит поглощение или излучение кванта энергии. Рассчитывая сопротивление металла, Вин приходит к формуле

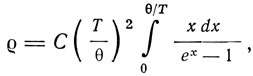
где kθ = hv_max.

Д. Д. Томсон также пришел к выводу, что теория электронного газа вообще несостоятельна, и противопоставил ей свою теорию электрических дублетов. Под действием электрического поля происходит поляризация атомов, и дублет приобретает потенциальную энергию - xedcosθ, где d - расстояние между зарядами диполя, а θ - угол,, образованный его осью с направлением поля. Корпускула "перепрыгивает" от одного атома к другому против направления поля, что приводит к появлению тока. Вычисляя среднее значение cos θ, можно получить плотность тока и электропроводность. При абсолютном нуле все дублеты располагаются по направлению поля ("насыщение"). Критическая температура перехода в сверхпроводящее состояние существует, по Томсону, только в том случае, если удельное сопротивление металла при обычной температуре больше ¹/₂₇₃. Сопротивление металла, по Томсону, пропорционально его тепловой энергии.

За год до публикации теории Томсона был опубликован в неоднократно упоминавшихся нами геттингенских докладах по теории материи и электричества доклад Г. А. Лоренца "Применение кинетической теории к движению электронов". Упомянув о теориях электропроводности Рикке, Друде и своей, в которых использовалось представление о свободных электронах со средней энергией ³/₂kT, и об их успехах, Лоренц продолжал:

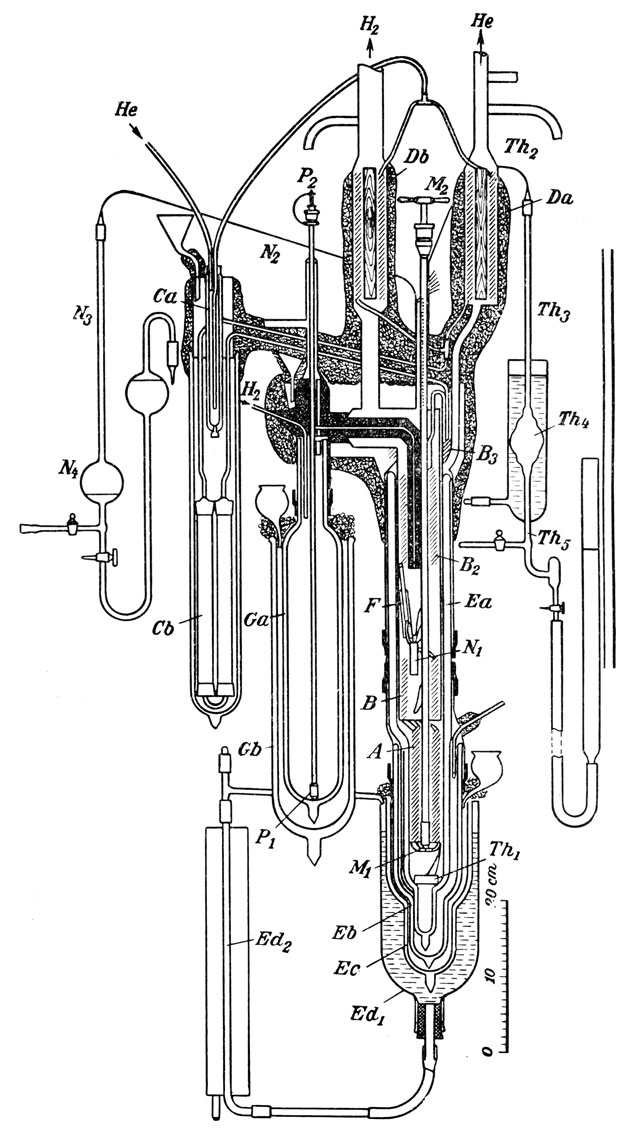
Схема аппарата для снижения гелия Каммерлинг-Оннеса

"Но постепенно им (т. е. этим теориям) стали противостоять значительные трудности, которые стимулировали предложение радикальных изменений. В недавно опубликованной работе (Лоренц имеет в виду появившуюся в 1913 г. работу Вина "К теории электрической проводимости в металлах") Вин идет даже так далеко, что полностью отказывается от представления о собственном тепловом движении, поскольку он приписывает электронам только скорость, не зависящую от температуры." Вин исходил из того факта, что теория электронного газа приводит к неверному закону Рэлея для теплового излучения. В связи с этим Лоренц замечает, что тепловое излучение возникает в процессе изменения скорости электрона при столкновении с атомами металла. Но механизм столкновения электрона с атомом еще неясен, и Лоренц выражает надежду, "что квантовой теории, коль скоро она введет подходящие представления для механизма столкновения, когда-нибудь удастся добиться удовлетворительного объяснения теплового излучения".

Вместе с тем Лоренц приводит аргументы в пользу гипотезы о свободных электронах в металле, скорость которых зависит от температуры. Так, он указывает, что анализ поведения электрона в поле черного излучения, сделанный им на Сольвеевском конгрессе 1911 г. и Фоккером в диссертации 1913 г., показывает, что средняя кинетическая энергия электрона в этом поле действительно пропорциональна температуре, хотя коэффициент пропорциональности получается меньше ³/₂ примерно в 24 раза. Он ссылается также на опыты Ричардсона по определению кинетической теории электронов, испускаемых нагретыми металлами, которые показывают, что находящиеся внутри металла свободные электроны обладают в среднем кинетической энергией ³/₂kT. Тем самым доказывается, что электроны в металле участвуют в тепловом движении. Вместе с тем значение теплоемкости металла при обычных температурах указывает на незначительность вклада электронов в эту теплоемкость. Поэтому Лоренц предполагает, что число свободных электронов в металле очень незначительно по сравнению с числом атомов. Остальные электроны следует считать неподвижными или, во всяком случае, обладающими кинетической энергией, значительно меньшей, чем ³/₂kT. Далее, Лоренц, ссылаясь на свою работу "О положительных и отрицательных электронах" (см. выше), указывает, что предположение о нескольких видах носителей тока противоречит второму закону термодинамики и что носителями тока являются только электроны. Он рассматривает затем механизм столкновения электронов с атомами. При этом он делает важное предположение, что электрон после столкновения покидает атом с той же скоростью, какой он обладал до столкновения. Направление же скорости остается совершенно неопределенным. Вполне возможно, что электрон при столкновении застревает в атоме, а взамен его атом испускает другой электрон с той же скоростью. Эта картина взаимодействия электронов с атомами напоминает позднейшие представления о столкновениях частиц с ядрами атомов.

Неопределенность направления скорости электронов после соударения приводит к тому, что в отличие от прежних теорий соотношение между теплопроводностью и электропроводностью металлов и зависимость этих величин от различных обстоятельств не могут быть указаны. Однако термоэлектрические величины должны удовлетворять соотношениям, выведенным из второго закона термодинамики. Лоренц исследует термоэлектрическую цепь сначала термодинамически, а затем прилагает к ней статистику Максвелла-Больцмана. При этом он приходит к выводу, что термодинамически полученное соотношение совпадает с соотношениями, выведенными из кинетической теории только в том случае, если для стационарного состояния справедлив закон распределения Максвелла. Вместе с тем для получения определенных значений характеристик металла, в частности коэффициента электропроводности, необходимы определенные допущения о механизме столкновения. Если воздержаться от таких допущений, то нельзя вывести и закон Видемана-Франца. Лоренц указывает, что посредством исследования соответствующих частных случаев можно даже показать, что этот закон вообще не справедлив и его следует рассматривать как приближенное правило.

Аппарат для сжижения гелия в лаборатории Каммерлинг-Оннеса в Лейдене

Свою статью Лоренц заканчивает любопытным примером. Он рассматривает электростатическую задачу о поле, создаваемом точечным зарядом, помещенным перед бесконечной проводящей плоскостью. Как известно, это поле совпадает с полем, произведенным данным зарядом и его "электрическим изображением" в плоскости. Заряд этого изображения распределен по плоскости с плотностью, убывающей обратно пропорционально третьей степени расстояния от центра. Но как будет выглядеть это распределение, если перед плоскостью помещен положительный заряд, равный элементарному заряду е? Лоренц указывает, что индуцированный отрицательный электрон будет быстро менять свое положение на плоскости и его распределение в среднем будет совпадать с распределением, даваемым электростатикой. Наблюдению доступно только это распределение. Это статистическое "распределение" электрона на поверхности было предшественником будущих статистических закономерностей квантовой механики.

Участвовавший в геттингенской дискуссии сотрудник Каммерлинга-Оннеса Биллем Гендрик Кеезом выступил с сообщением "О применении квантовой теории к теории свободных электронов в металле". Кеезом замечает, что квантовая теория может быть применена к свободным электронам в металлах таким же образом, как она была применена Тетроде и Ленцем к идеальному газу, если ввести дополнительно нулевую энергию. Поскольку в системе свободных электронов частоты, соответствующие скоростям электронов, значительно выше, чем частоты, появляющиеся для идеальных газов, следствия, получающиеся для идеальных газов при крайне низких температурах, будут применимы для электронов при экспериментально достигаемых температурах. Для высоких температур энергия свободных электронов совпадает с даваемой теорией Друде-Лоренца, но для низких температур энергия и, следовательно, средняя скорость приближаются к конечному постоянному значению, что соответствует предположению Вина в его теории электропроводности. Тем самым устраняются затруднения с теплоемкостью и нет необходимости принимать малое число свободных электронов. Число свободных электронов при низких температурах приближается к постоянному значению, как это принимает Вин в своей теории. Таким образом, применение квантовой теории, по Кеезому, дает результаты, согласующиеся при низких температурах с теорией Вина. В 1915 г. Лоренц, суммируя кратко положения электронной теории металлов, заключал: "Впрочем, в области, которой мы кратко коснулись, имеется еще много нерешенных проблем, из которых некоторые представляют значительные трудности, поскольку, как вообще должно быть признано, физические теории до настоящего времени проникли в сущность материи еще очень поверхностно".

Однако это проникновение в сущность материи уже началось и многие результаты электронной теории проводимости были только незначительно модифицированы квантовой теорией металлов, что, конечно, не означает недооценки глубокого принципиального значения изменений, внесенных в теорию проводимости квантовой теорией. На эту теорию, как мы видели, возлагал надежды и Лоренц.