Магнетизм

Электронная теория не только вывела законы постоянного тока из состояния чисто эмпирических фактов, но и дала возможность теоретического объяснения явлений магнетизма, в которых длительное время господствовала чистая эмпирия. Эренфест отмечал, что электронная теория превратила "безнадежно хаотическую" область ферромагнетизма в область "истинной" физики.

П. Ланжевен

Начало проникновения электронной теории в магнетизм было положено статьей Поля Ланжевена "Магнетизм и теория электронов", опубликованной в 1905 г. Однако у Ланжевена были предшественники, о которых он сам упоминает в своей статье, и мы должны вкратце рассмотреть попытки построения теории магнитных явлений до Ланжевена.

Прежде всего, мы должны упомянуть теорию элементарных магнитов В. Вебера, разработанную в 1864 г. Вебер принимает, что частицы железа или другого ферромагнитного вещества представляют собой магнитики с магнитным моментом m, оси которых ориентированы в ненамагниченном состоянии беспорядочным образом. Под действием поля напряженностью X оси магнитиков будут поворачиваться, однако при этом они подвергаются действию молекулярной направляющей силы D, которая стремится уменьшить угол поворота α. Условие равновесия обеих сил, действующих на магнит, имеет вид:

где α - угол, образованный первоначальным направлением оси магнитного поля, β - угол, на который поворачивается ось магнита под действием поля, φ = β - α - угол, образованный новым положением магнита с направлением магнитного поля. Отсюда вычислением получаем для результирующего магнитного момента единицы объема магнитика I из выражения

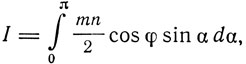
где n - число магнитов в единице объема. Для X<D значение

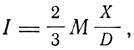
и для X>D

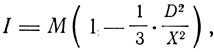
где М = nm - магнитный момент единицы объема при полном насыщении. Отсюда следует, что интенсивность намагничивания I растет пропорционально магнитной силе до тех пор, пока последняя не достигает значения D, и при дальнейшем возрастании магнитной силы стремится к постоянному значению насыщения: I₀ = М. Однако на опыте этой пропорциональности для малых значений поля в ферромагнетиках нет. Кроме того, как было выяснено исследованиями Варбурга (1886), Гопкинсона (1885) и Юинга (1885), на опыте наблюдается остаточное намагничивание и при цикличном изменении напряженности магнитного поля кривая намагничивания будет замкнутой (петля гистерезиса). Эти факты теорией Вебера не объясняются. Юинг, который ввел в науку термин "гистерезис", видоизменил теорию Вебера, допустив взаимодействие между отдельными элементарными магнитами, благодаря которому они располагаются определенными группами. Такие группы устойчивы, если только внешнее магнитное поле не превосходит некоторой определенной величины. При увеличении поля выше значения этой величины получается новое расположение групп. При дальнейшем увеличении поля группы приходят в неустойчивое равновесие и новое, даже незначительное увеличение поля приводит к тому, что оси всех магнитов становятся параллельными между собой и почти параллельными полю. Наконец, при дальнейшем увеличении поля оси магнитов становятся параллельными полю, достигается магнитное насыщение. При уменьшении поля магниты в группах сохраняют свою ориентацию и лишь несколько поворачиваются благодаря взаимному влиянию. Ориентировка магнитов в отдельных группах сохраняется и при уменьшении внешнего поля до нуля, что приводит к остаточному намагничиванию. Юинг иллюстрировал свою теорию опытами с системами магнитных стрелок. При этом обнаружилось, что в отсутствие поля стрелки располагаются отдельными группами. Подвергая эти группы действию магнитного поля, Юинг наблюдал изменение ориентации магнитов в отдельных группах вплоть до полного насыщения, когда все стрелки были параллельны друг другу и внешнему полю.

Юинг изложил свою теорию в 1890 г. Его идея внутреннего взаимодействия между магнитиками получила в дальнейшем развитие во взглядах Вейсса, а впоследствии было получено непосредственное доказательство существования в ферромагнетиках отдельных областей намагничивания - доменов.

В 1894-1895 гг. исследованием слабо магнитных тел (диамагнетиков и парамагнетиков) занимался Пьер Кюри. Исследуя силы, действующие на слабо магнитные тела в неоднородном поле, он установил следующие законы:

1. Удельная восприимчивость диамагнитных тел не зависит от температуры.
2. Очень часто она не зависит от агрегатного состояния тела.
3. Массовая восприимчивость парамагнитных тел обратно пропорциональна абсолютной температуре
   γ = ^С/_Т

Постоянная С называется "постоянной Кюри".

Исключение из первого закона Кюри составляет висмут, диамагнитная восприимчивость которого уменьшается почти линейно с увеличением температуры. Д. Д. Томсон в 1900 г. предположил, что диамагнетизм висмута обусловлен наличием свободных электронов (корпускул), сообщающих ему электропроводность. Внешнее магнитное поле искривляет их пути свободного пробега и тем самым сообщает висмуту диамагнетизм. Э. Шредингер в 1912 г. обработал математически эту идею и показал, что свободные электроны могут быть причиной диамагнетизма. Диамагнитная восприимчивость, обусловленная свободными электронами, по Шредингеру, пропорциональна Nλ², где N - число свободных электронов в единице объема металла, λ - длина свободного пробега электрона. Величина Nλ² зависит от температуры и в такой же степени зависит от температуры магнитная восприимчивость. В квантовой теории диамагнетизм свободных электронов был вычислен Л. Д. Ландау (диамагнетизм Ландау).

П. Кюри

Эффект Зеемана с точки зрения электронной теории объяснялся орбитальным движением электронов. Электронная орбита явилась реализацией амперовых молекулярных токов. Таким образом, получалась реальная возможность объяснить магнитные свойства веществ с помощью представления об электронных орбитах. Эту возможность рассматривали в 1902 г. В. Фогт и в 1903 г. Д. Д. Томсон. Оба независимо друг от друга пришли к выводу, что "гипотеза об электронах, движущихся без торможения, не может дать никакого представления об явлениях постоянного магнетизма или диамагнетизма".

"Я хотел бы,- пишет в связи с этим Ланжевен,- показать здесь, каким образом, вопреки мнению Томсона и Фогта, я считаю возможным посредством электронной гипотезы уточнить идеи Ампера и Вебера} найти для пара- и диамагнетизма требуемые совершенно различные объяснения и, наконец, осветить с этой точки зрения вопрос о магнитной энергии в целом". Основные результаты своего исследования магнитных свойств вещества Ланжевен изложил в докладе "Физика электронов", который он сделал 22 сентября 1904 г. на конгрессе в Сен-Луи.

Прежде всего, он установил, что внутримолекулярный ток, обусловленный движением электронов, эквивалентен магниту с магнитным моментом M = ^eS/_τ, где S - площадь, охватываемая электронной орбитой, τ - период обращения электрона. "Подобный молекулярный ток,- говорил Ланжевен в своем докладе,- соответствовал бы каждому из электронов, находящихся в молекуле, и результирующий из него магнитный момент мог бы быть равным нулю или отличающимся от нуля, в зависимости от степени симметрии молекулярного здания".

Диамагнетизм Ланжевен объясняет следующим образом: "Если на поле группы таких молекул наложить внешнее магнитное поле, то все молекулярные токи подвергнутся изменению, независящему от того способа, каким произведено это наложение, - только ли установлением дополнительного поля или же смещением молекул в ранее установленном магнитном поле. Направление этого изменения, произведенного в молекулярном токе благодаря индукции, всегда соответствует диамагнетизму, причем приращение магнитного момента М будет

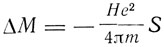
для случая кругового тока, где Н - слагающая магнитного поля, нормальная к плоскости орбиты, a m - масса электрона". Этот диамагнитный эффект существует всегда, но в парамагнетиках маскируется более сильным действием, обусловленным результирующим магнитным моментом молекул. Поскольку диамагнетизм является внутриатомным свойством, диамагнитная постоянная, как этого требует закон Кюри, не зависит или очень мало зависит от температуры. Для круговых орбит, средний квадратичный радиус которых равен r₁, Ланжевен находит

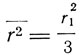
и соответственно коэффициент магнитной восприимчивости

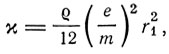
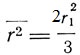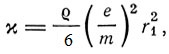где = Ne. Однако в расчет Ланжевена вкралась ошибка. На самом деле, и Ланжевен оценивает величину r₁ неравенством 2*10^-10<r₁<10^-8 и этими малыми размерами r₁ объясняет малую величину диамагнитного эффекта. Ланжевен подчеркивает, что если нет взаимных соударений молекул, то "даже если молекула обладает результирующим моментом, не проявляется ничего, кроме явления диамагнетизма... Первоначальный эффект при создании внешнего магнитного поля состоит во всех случаях в диамагнитной поляризации вещества". Ланжевен связывает с диамагнетизмом эффект Зеемана. "Наконец, я настаиваю на том, что явление Зеемана представляет собой один из видов диамагнитного процесса",- писал он. При этом он считает орбиты электронов круговыми, не деформируемыми и имеющими сопротивление, равное нулю. Эти орбиты Ланжевена - предшественники бо-ровских стационарных орбит. Парамагнетизм обусловлен наличием в молекулах магнитного момента. Ланжевен рассматривает газообразный парамагнетик, например кислород, и исследует, "какова будет намагниченность под влиянием ориентации молекул, вызванной полем H". Применяя к поведению молекул в магнитном поле статистическое распределение Больцмана, Ланжевен находит для результирующего магнитного момента I единицы объема (интенсивность намагниченности) известное выражение

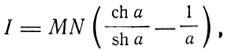
где М - магнитный момент молекулы, N - число молекул в единице объема,

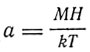
(Ланжевен вместо k употребляет обозначение r). Для малых полей H, используя разложение в ряд гиперболических функций, получаем

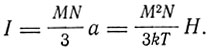
Отсюда коэффициент магнитной восприимчивости

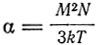
оказывается обратно пропорциональным абсолютной температуре, как того требует закон Кюри. При насыщении

и магнитная восприимчивость

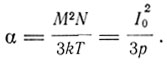
По данным Кюри, для нормального давления р = 10⁶ и 0°С, α = 1, 43*10^-7 и I₀ = 0,05. Для жидкого кислорода, плотность которого в 500 раз больше газообразного, I₀>325, что объясняет сильный магнетизм жидкого кислорода.

Теория Ланжевена проложила путь к пониманию сложных явлений магнетизма. Она впервые использовала в качестве рабочей гипотезы идею стационарных электронных орбит, сыгравшую такую важную роль в истории атомной физики. Наконец, она в необычайной степени стимулировала развитие теории магнетизма. Пример Ланжевена вдохновил на поиски теоретических основ ферромагнетизма. Через два года после появления работы Ланжевена Пьер Вейсс положил начало теории ферромагнитных явлений.

Вейсс исходил из аналогии парамагнитных явлений с явлениями в идеальных газах. "Кинетическая теория Ланжевена,- писал он в 1911 г.,- является для парамагнетизма тем же, что теория Даниила Бернулли для сжимаемости газа". Но теория реальных газов ван дер Ваальса в отличие от теории идеальных газов вводит взаимодействие молекул, "результатом которого является внутреннее давление в жидкостях и газах". "Аналогичным образом я ввел молекулярное поле, добавляемое к внешнему полю, которое с помощью законов парамагнетизма объясняет сильное намагничивание ферромагнитных тел".

"Я принимаю,- пишет далее Вейсс,- что действие совокупности молекул на одну из них эквивалентно однородному магнитному полю, интенсивность которого

пропорциональна намагничиванию и которое направлено так же, как оно".

Вейсс указывает, что такое уподобление молекулярного действия магнитному полю вводится только для удобства. Природа молекулярных сил совершенно неопределенная, и Вейсс полагает, что эти силы не являются магнитными. Итак молекулярное поле Вейса пропорционально намагничиванию:

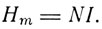
Если ввести вместо I намагничивание грамм-молекулы от, то

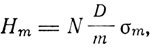
где D - плотность вещества, m - его молекулярный вес. Полное поле складывается из внешнего поля Не и внутреннего молекулярного поля Н_m: H = H_e+H_m. Параметр Ланжевена

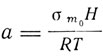
(его значение берется для грамм-молекулы) определяется всем полем. В отсутствие внешнего поля

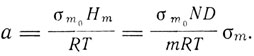
На графике Ланжевена, на котором нанесено значение 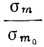в зависимости от а, это соотношение изобразится прямой линией. Точка пересечения этой прямой с кривой Ланжевена

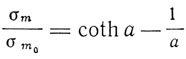
соответствует намагничиванию в отсутствие внешнего поля - спонтанному намагничиванию.

Чтобы совместить идею спонтанного намагничивания с нейтральным состоянием ферромагнетика в отсутствие поля, Вейсс предполагает, что ферромагнетик состоит из множества небольших областей спонтанного намагничивания, направления намагничивания которых распределены хаотически, что обеспечивает нейтральность ферромагнетиков в целом. Поэтому роль внешнего поля заключается не в создании намагничивания, а в ориентации областей спонтанного намагничивания по направлению поля. Таким образом, при данной температуре спонтанное намагничивание совпадает с интенсивностью насыщения. При возрастании температуры прямая становится более крутой и намагничивание не убывает. При некоторой температуре 6 прямая соприкасается с кривой Ланжевена и интенсивность спонтанного намагничивания становится равной нулю. Для этой температуры П. Вейсс и Каммерлинг-Оннес ввели в 1910 г. название "точка Кюри". Для определения точки Кюри θ используется соотношение

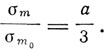
Когда Т стремится к Θ^σ_m/_σm0 и а одновременно стремится к 0. Отсюда

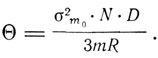
Константа Кюри

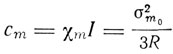
и

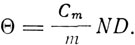
Вместе с тем закон Кюри для ферромагнетиков принимает форму закона Кюри-Вейсса:

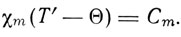
"Таким образом,- пишет Вейсс,- если для чисто парамагнитных тел константу Кюри образуют, умножая коэффициент намагничивания на абсолютную температуру, для ферромагнитного тела эту константу получают, умножая измеренный выше точки Кюри коэффициент намагничивания на избыток температуры наблюдения над температурой этой точки".

Вейсс указывает, что установленный им закон представляет значительный интерес еще потому, что дает простой и точный метод экспериментальной проверки теории. Уже в первой работе Вейсс указал на удовлетворительное согласие теории с опытом; еще более обширные данные, характеризующие согласие теории с опытом, были приведены в работе Вейсса и Фёкса в 1911 г. Однако Вейсс обращает внимание на то обстоятельство, что, несмотря на такое поразительное подтверждение теории, существуют факты, показывающие недостаточность теории в ее современной форме. Эти факты были обнаружены в работе Вейсса и Каммерлинг-Оннеса в 1910 г., где они исследовали ход температурной зависимости интенсивности насыщения железа, никеля, кобальта и магнетита при низких температурах. Эта зависимость является индивидуальной для каждого вещества.

Но Вейсс полагает, что его теория содержит значительную долю истины и покоится на очень простых основаниях. Эти основания связывают ланжевеновский магнитный момент молекулы и массу молекулы с введенным Вейсом молекулярным полем N. Вейсс пытался сперва выразить N как функцию температуры и намагничивания, но результат получился мало удовлетворительным. Тогда, обратив внимание на тот факт, что в опытах с магнетитом прямые, представляющие выше точки Кюри ¹/_χ как функции температуры испытывают внезапное изменение направления, Вейсс пришел к идее изменения состояния, возбуждаемого самой молекулой. Вейсс предполагает, что это изменение скорее обусловлено изменением массы молекулы (полимеризация), чем ее магнитного момента. Он и Каммерлинг-Оннес показали, что магнитный момент молекулы может быть определен очень точно путем измерения интенсивности насыщения в жидком водороде. Они предположили, что этот магнитный момент является фундаментальной величиной вследствие своей, по крайней мере, относительной неизменяемости. Опыт показал, что магнитные моменты трех металлов находятся в простых рациональных отношениях друг к другу, что доказывает фундаментальный характер этой величины и одновременно существование в каждом атоме магнитного момента, содержащегося целое число раз. Так появился магнетон Вейсса. По измерениям Каммерлинг-Оннеса и Вейсса, в грамм-атоме железа содержится 11 магнетонов, в никеле 3. При этом грамм-магнетон оказывается равным 1123,5. Взяв для числа Авогадро значение Перрена (1910) 68,5*10²², Вейсс находит магнитный момент одного магнетона, он равен 16,40*10^-22. Так в физику магнетизма вошла идея атомности магнитного момента. Эта идея не могла не привлечь внимания Бора. Как мы уже упоминали в предыдущей главе, Бор, заканчивая первую серию своих статей о строении атома (точнее, третью часть одной статьи), писал: "Тесная связь настоящей теории с современной теорией излучения черного тела и удельной теплоемкости очевидна; кроме того, поскольку по обычной электродинамике магнитный момент, обусловленный электроном, вращающимся по круговой орбите, пропорционален угловому моменту, мы должны ожидать также тесной связи с теорией магнетонов, предложенной Вейссом".

Бор обещал вернуться к разработке теории магнитных явлений позже. И, действительно, в следующем, 1914 г. концепция магнетона Бора утвердилась в квантовой физике. Величина магнетона Бора выражается формулой

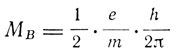
и составляет 9,23*10^-21 электромагнитных единиц, что почти точно равно 5 магнетонам Вейсса. На этот факт обратили внимание как сам Бор, так и другие. В частности, на собрании Британской ассоциации в Бирмингаме, происходившем осенью 1914 г., Чалмерс особо подчеркнул это обстоятельство. На этом же собрании с кратким докладом о теории магнитов выступил Мак Лорен. Он утверждал, что магнитные явления не могут быть объяснены теорией классического электрона на основе обычных законов и обратил внимание на то, что даже Ланжевену при объяснении парамагнетизма пришлось вернуться к концепции магнитного диполя. Внешнее магнитное поле, действуя на такой диполь, совершает работу, тогда как сила Лоренца, действующая на движущийся электрон, работы не совершает. По мнению Мак Лорена, этот факт сам по себе требует дальнейших исследований. Он даже утверждал, что "парамагнетизм остается тайной". Мак Лорен полагал, что электрон и магнетон имеют равные права в объяснении природы материи, которая сама является просто границей электромагнитного поля; электрон и магнетон не должны объясняться друг через друга и являются просто внутренними границами электромагнитного поля, однако все эти попытки истолковать магнетизм в духе классических гипотез потерпели неудачу. Только развитие квантовой теории дало возможность дать правильную интерпретацию парамагнитных и ферромагнитных явлений. Но это относится уже к следующему периоду развития квантовой теории.