Теория Зоммерфельда

Бор продолжал в работах 1914-1915 гг. рассматривать теорию водородных атомов. Важнейшим итогом его работ явилось установление принципа соответствия (1918), зародыш которого, как мы видели, был уже в ранних статьях Бора. В 1915 г. одновременно и независимо друг от друга Вильям Вильсон в Англии", Арнольд Зоммерфельд в Германии и Ишивара в Японии начали рассмотрение с точки зрения квантовой теории некруговых орбит. Обобщенные квантовые условия для периодических систем, допускающих разделение переменных, были сформулированы Вильсоном и Зоммер-фельдом в форме

где слева стоит фазовый интеграл для переменной q. Зоммерфельд, приведя в своей работе, о которой мы будем говорить дальше, это правило квантования, писал: "Я дружески был осведомлен, что г. Вильсон (W. Wilson, Phil. Mag. Июнь. 1915) уже раньше сформулировал, как и я, квантовое условие (1) и притом по форме в точности совпадающие с (1), включая правило о пределах интеграции. В качестве единственного применения г. Вильсон рассматривал, с добавлением некоторых дальнейших гипотез, закон черного излучения. Во второй заметке (Phil. Mag. Ноябрь. 1915) он вычислил мимоходом фазовый интеграл для r-й координаты кеплеровского эллипса, совпадающий с уравнениями (9) и (10) нашего § 4. Однако он не вывел отсюда определенных следствий для понимания серии Бальмера. Работа г. Ишивара, на которую ссылается г. Вильсон, мне не была известна".

А. Зоммерфельд

Итак, как нередко случалось в истории физики, одна и та же проблема стала разрабатываться независимо друг от друга несколькими исследователями. Это свидетельствует об актуальности проблемы. Наибольших успехов добился Зоммерфельд, исследования которого составили ядро его будущей знаменитой книги "Строение атома и спектры". Первое сообщение о своих результатах Зоммерфельд опубликовал в 1915 г. в "Известиях Баварской Академии" в Мюнхене. Подробное изложение работы появилось в 1916 г. в 51-м томе "Annalen der Physik" под заглавием "К квантовой теории спектральных линий".

Работа состояла из трех частей: I. Теория серии Бальмера. II. Тонкая структура водородных и водоро-доподобных линий. III. Теория рентгеновских спектров. Первая часть работы начинается с указания, что теория Бора существенно дополняется введением некруговых орбит. Далее Зоммерфельд формулирует общий принцип теории спектральных серий: "Стационарные орбиты электронов в атоме (и в дальнейшем в молекуле) не образуют континуума, а представляют некоторую сетчатую конструкцию. Фазовое пространство, как множество всех мыслимых, в том числе и нестационарных состояний, пронизано петлеобразно фазовыми кривыми стационарных орбит. Размеры петель определяются Планковской h".

Вместе с тем Зоммерфельд выписывает общую формулу спектральных серий в виде

где N - постоянная Ридберга. Как видно, Зоммерфельд предполагает, что спектральные термы определяются двумя квантовыми числами n и n'.

Зоммерфельд начинает свое исследование с утверждения, что элемент фазового пространства имеет в квантовой теории конечную величину h^f, где f - число степеней свободы системы. Это утверждение он приписывает Планку, хотя, как мы видели раньше, сам Планк называет автором этого постулата Саккура. Зоммерфельд выбирает координаты системы q_i таким образом, чтобы получить из квантового принципа Саккура-Планка f отдельных условий для каждой степени свободы. Эти квантовые уравнения Зоммерфельда имеют вид

Он указывает, что эти уравнения приводят к тому же результату, что и общий принцип Планка - Саккура:

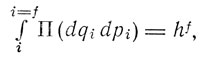
но работать с ними значительно удобнее. Зоммерфельд считает свои уравнения таким же недоказуемым основным принципом квантовой теории, как и принцип Саккура-Планка. Для применения квантовых условий Зоммерфельда нужно выбрать подходящим образом координаты, а также обладать правилом определения пределов интегрирования для каждой координаты. Общего правила для выбора координат, как подчеркивает Зоммерфельд, дать нельзя, надо накопить опыт на частных примерах. Что же касается пределов интегрирования, то для их определения Зоммерфельд дает следующее правило: "Интегрирование для каждой координаты q должно распространяться на всю область значений q, пробегаемых при однозначной характеристике фазы системы". В более ранних работах Зоммерфельд ограничивался рассмотрением периодических движений, для которых пределы интегрирования определялись периодом. Новая формулировка позволяет рассматривать и квазипериодический релятивистский кеплеровский эллипс.

Зоммерфельд придает своим квантовым условиям более удобную форму. Начертив на фазовой плоскости фазовые кривые, удовлетворяющие квантовым условиям, находим для площади между n-й и (n-1)-й кривой

Полагая n = 1, 2, ..., получим

Суммируя, найдем ∫(p_n - p₀)dq = nh и, выбирая начальную кривую так, что ∫p₀dq = 0, получим

Фазовый интеграл для каждой координаты должен равняться целому кратному кванта действия. Применяя это правило к осциллятору, получаем условие Планка

Для ротатора получаем

где р = ma²ω - момент количества движения. Квантование вращательного момента было, как мы знаем, введено Эренфестом в 1913 г. Для кеплеровского эллипса получаются азимутальные квантовые условия

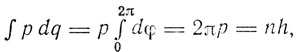
причем

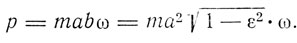
Для радиального фазового интеграла вычисления дают

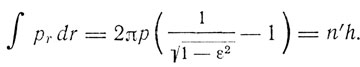
Отсюда, имея в виду условие (1), получаем

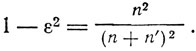
Боровское условие частот

для кеплеровского эллипса принимает вид

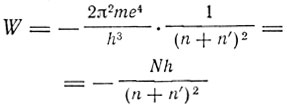
(III)

и, следовательно,

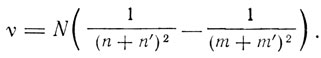
Таким образом, опять получается бальмеровская серия, причем энергетические уровни зависят от числа n+n'. "Кажется исключенным,- пишет Зоммерфельд,- что такой точный и богатый следствиями результат можно приписать алгебраической случайности". Одному и тому же значению энергии соответствует несколько эллиптических орбит (вырождение энергетических уровней), параметры которых определяются равенствами:

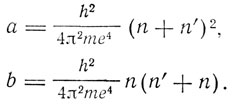
Для n' = 0 получаем круговую орбиту, для n = 0 - маятникообразную орбиту, проходящую через ядро, что недопустимо ни по геометрическим, ни по динамическим соображениям, и Зоммерфельд исключает этот случай из рассмотрения. Для дальнейших значений квантовых чисел n + n' получается ряд эллипсов, так что число возможных случаев возбуждения спектральной линии равно NM, где N = n + n', M = m + m'. В действительности, однако, число способов возбуждения будет иным. "Но, во всяком случае, водородная линия в нашем понимании появляется в результате достаточно сложного наложения различных дискретных процессов".

Далее Зоммерфельд пытался сформулировать правило отбора, позволяющее уменьшить число возможных переходов NM. Он предупреждает, что высказываемые им соображения являются гипотетическими. Первое положение, определяющее отбор переходов, исходит из того, что энергия, с одной стороны, положительная величина, с другой стороны, в спонтанных процессах должна уменьшаться. Отсюда

Так как фазовые интегралы, зависящие от квантового числа п, являются также положительными, то Зоммерфельд постулирует, что при спонтанных переходах эти интегралы, так же как и энергия, убывают. Таким образом, при спонтанных переходах ни одно из квантовых чисел не может возрастать, следовательно,

Эти условия уменьшают число возможных переходов. Зоммерфельд полагает, что при m + m' = M, n + n' = N число допускаемых переходов равно N(M - ^N-1/₂). Правила отбора, таким образом, Зоммерфельдом еще не сформулированы, но опыт подсказывает ему необходимость ограничения возможных переходов, приводящих к возникновению спектральных линий. Эти ограничения связаны с вопросом об интенсивности спектральных линий. Зоммерфельд формулирует правило интенсивности в следующих выражениях: для интенсивности линии, которой соответствует переход от (m, m') к (n, n') при условии, что этот переход не запрещен квантовыми неравенствами, интенсивность равна

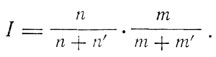
При этом интенсивность наиболее яркой линии, соответствующей переходу с одной круговой орбиты на другую, принимается за единицу. При нарушении неравенств m ≥ n, m' ≥ n' интенсивность будет малой или даже нулевой. Зоммерфельд указывает на предварительный характер сформулированного им правила интенсивности. Он замечает, что квантовые уравнения и вопросы интенсивности зависят от деталей возбуждения свечения и вряд ли они подчиняются такой простой и общей теории, какой подчиняется положение спектральных линий. Затем Зоммерфельд рассматривает проблему пространственного квантования. Для определения положения электрона в пространстве вводятся сферические координаты r, υ, ψ, которым соответствуют квантовые условия:

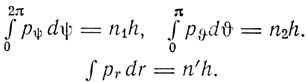
Последний интеграл берется в пределах от r_min до r_max, и его вычисление дает

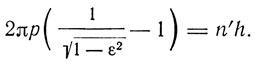
Для первого интеграла имеем p_ψ = р cos α и, следовательно,

Величина р_υ = mr²υ. Таким образом, получаются следующие уравнения пространственного квантования:

Следовательно,

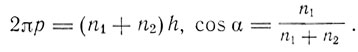
Таким образом, наклон орбиты по отношению к некоторой оси определяется дискретными числовыми значениями. Если n₁ + n₂ = n, то cos α принимает n+1 значений и полное число значений α равно 2n+1. На этом результате основана теория нормального эффекта Зеемана, созданная Зоммерфельдом и независимо от него Дебаем в том же, 1916 г. В примечании при корректуре своей работы Зоммерфельд ссылается на свою статью об эффекте Зеемана, опубликованную им в журнале "Pysikalische Zeitschrift". Статья называлась "К теории эффекта Зеемана линий водорода с добавлением об эффекте Штарка". Теория эффекта Штарка была дана в 1916 г. П. С. Эпштейном. Для того чтобы представить импульсы в виде функций соответствующих им координат (p_i = p_i(q_i)), Эпштейн для изучения движения водородного атома в электрическом поле ввел параболические координаты. Тогда квантовые условия записываются в виде

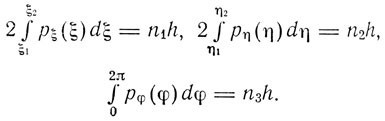
Отсюда получаются выражения для энергии электрона, которую Эпштейн обозначает через А

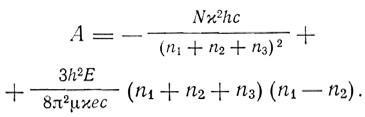
Здесь N - постоянная Ридберга, אe - заряд ядра, Е - напряженность электрического поля. Таким образом, влияние электрического поля сказывается в увеличении числа энергетических уровней атома, что и приводит к расщеплению спектральных линий в электрическом поле. Вырождение уровней, существовавших до появления электрического поля, снимается. Изменение частоты, обусловленное полем, выражается уравнением

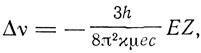
где

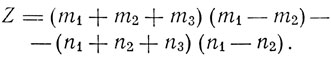
Числа тип соответствуют начальной и конечной орбите. Как видим, расщепление пропорционально Е и симметрично, т. е. для каждого положительного Δv имеется соответствующее отрицательное - Δv. Эти факты были установлены Штарком. Для водорода коэффициент при EZ равен 6,43*10^-5, если Е выражено в вольтах на сантиметр. Смещение, выраженное в длинах волн, будет

При этом число Z ограничено неравенствами Зоммерфельда:

Совпадение теории с опытом, как отмечает Эпштейн, "блестящее". Вместе с тем обнаруживаются линии, "запрещенные" неравенствами Зоммерфельда. "Интересно, что первые два неравенства выполняются строго, между тем как третье... которое относится к азимуту ξ, по-видимому, справедливо лишь в грубых чертах". Это обстоятельство, отмеченное Эпштейном, отмечается и Зоммерфельдом в разбираемой нами работе. "Что касается поляризации,- пишет Эпштейн,- то подтверждается следующее в высшей степени замечательное эмпирическое правило: четная разность азимутальных квантовых чисел m₃ - m₂ ведет к параллельной (р) поляризации, нечетная - к перпендикулярной.

Это правило справедливо во всех случаях без исключения, хотя у нас и нет решительно никаких путей к его пониманию". "Как бы то ни было,- заключает Эпштейн свое изложение теории эффекта Штарка,- ...результаты теории явления Штарка... дают одно из наиболее решительных доказательств в пользу учения о квантах и того применения этого учения к атомистике, которое сделано Бором". К работе Эпштейна по штарк-эффекту Зоммерфельд неоднократно возвращается в своей статье, равно как и к работе Шварцшильда, разработавшего в том же, 1916 г. теорию эффекта Штарка независимо от Эпштейна. Эти исследования связаны с общими принципами динамики, и Зоммерфельд посвящает обследованию этой связи специальный параграф своей работы. Квантовое условие (I)

не дает указаний на выбор координат. Эпштейн в своем исследовании штарк-эффекта исходил из уравнения Гамильтона-Якоби общей динамики:

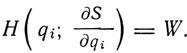
(Эпштейн обозначал энергию W через А, функцию действия S через W.) Функция действия S тесно связана с фазовыми интегралами. Так как

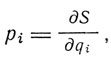
то 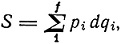где f - число степеней свободы.

"Таким образом,- пишет Зоммерфельд,- функция действия Якоби есть сумма наших фазовых интегралов по всем степеням свободы системы". Понятия и методы динамики Гамильтона-Якоби поэтому с успехом могут быть использованы в квантовых задачах. При подходящем выборе переменных уравнение Гамильтона-Якоби может быть проинтегрировано методом разделения переменных, посредством выражения

где каждая отдельная функция S_i зависит только от одной координаты q_i и, кроме того, от f постоянных интеграции α_k. Такие разделяющиеся переменные Эпштейн считает подчиняющимися квантовому принципу:

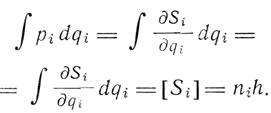
При этом [S_i] обозначает модуль периодичности функции S_i, т. е. приращение, испытываемого S_i, когда q_i пробегает всю необходимую для представления всех фаз движения область. Таким образом, движения, выделяемые квантовыми условиями, являются такими движениями, для которых модули периодичности функций действия являются целыми кратными кванта действия h. Именно таким образом Эпштейн выбирал параболические координаты для описания эффекта Штарка. Вместе с тем энергия W (или А у Эпштейна) определяется посредством квантовых условий

и будет величиной, дискретной во всех случаях, где можно найти координаты, относительно которых разделяется дифференциальное уравнение Якоби. Тем самым разделение переменных в уравнении Якоби является достаточным, чтобы получить резкие спектральные линии. Необходимость же этого условия остается под вопросом, на который едва ли можно ответить, как замечает Зоммерфельд.

"Мы исследовали,- заключает этот параграф Зоммерфельд,- связь квантовой теории с методами общей механики, примыкая к изложению Эпштейна. С тем же правом мы могли привлечь изложение Шварцшильда. Действительно,

Шварцшильд развил те же самые идеи, как и Эпштейн. Но Шварцшильд ограничил свою формулировку квантового . принципа "условно-периодическими движениями*. Итак, в работах Эпштейна, Шварцшильда и Зоммерфельда квантовая теория была связана с теорией Гамильтона-Якоби классической механики. Эта связь оказалась необычно плодотворной ив измененной форме вошла и в новую квантовую механику Гейзенберга и Шредингера.

Вторая часть статьи Зоммерфельда посвящена вопросу о тонкой структуре спектральных линий. Прогресс спектроскопической техники, выразившийся в построении приборов с высокой разрешающей способностью, привел к обнаружению тонких дублетов и триплетов спектральных линий. Эти тонкие факты и подверг теоретическому анализу Зоммерфельд во второй части своей статьи. Этот анализ был основан на идеях теории относительности, и в первых изданиях его книги "Строение атома и спектры" находился параграф, посвященный изложению основных идей специальной теории относительности.

Впервые на значение теории относительности для строения атома указал Бор в своей статье 1915 г. Он же предложил рассматривать дублет водородных линий как релятивистский эффект второго порядка отношения ^ν/_c. В своей теории Зоммерфельд опирался на расчеты релятивистского кеплеровского движения, проведенные в работах Вакера 1909 г. и Визниевского 1913 г. для движения планет. Основные моменты расчета содержатся в уравнениях:

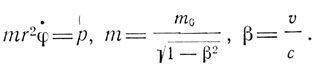
(1)

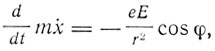
(2)

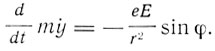
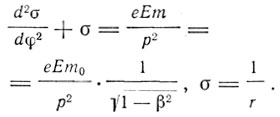
(3)

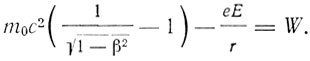
(4)

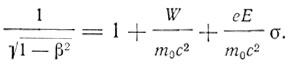
(5)

Из уравнений (5) и (3) следует дифференциальное уравнение движения электрона в полярных координатах:

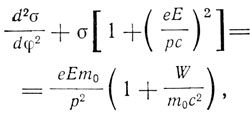
интеграция которого дает

где

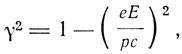
(6)

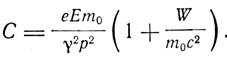
Таким образом, орбита оказывается эллипсом с движением перигелия. Если в начальный момент φ = 0 электрон находился в перигелии, то уравнение траектории имеет вид

Если же при φ = 0 электрон находился в афелии, то

Введем обозначения

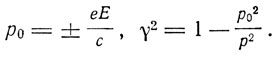
(8)

Движение перигелия будет зависеть от отношения ^p₀/_p. Оно будет медленным и орбита будет эллипсообразной, если p>>p₀. В случае же p→p₀ орбита будет спиральной и теряет всякое сходство с эллипсом. Отсюда видно важное значение "универсального момента" p₀, который для атома водорода (E = eе) равен р₀ = ^e2/_c. Зоммерфельд вводит отношение α этого момента к наименьшему квантовому значению p₁ = ^h/_2π углового момента:

Он указывает, что Эйнштейн еще в 1911 г. заметил, что ^e2/_c имеет размерность h, и думал, что h сводится к этой величине. Препятствием было наличие большого числового множителя между этими величинами. Джинс полагал в 1915 г., что h (4яе)2

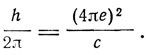
К этим справкам Зоммерфельда мы добавим, что еще Лармор в 1900 г. установил соотношение

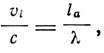
где υ₁ - скорость орбитального движения электрона в атоме, l_α - диаметр орбиты и это соотношение, если подставить вместо υ₁ и l_α их значения, из теории Бора дает величину α. Зоммерфельд заканчивает параграф, в котором вводится величина α, словами: "Теперь мы видим, что этот числовой множитель, названный выше а, является фундаментальной величиной для описания тонкой структуры спектральных линий".

Из квантовых условий

Зоммерфельд получает азимутальное квантовое условие

и радиальное квантовое условие в виде

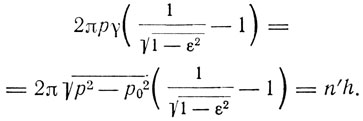
Вычисления приводят к следующему соотношению для энергии:

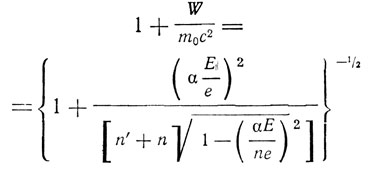
Отсюда получаем частоты спектральных линий:

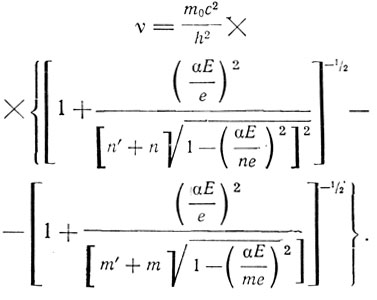
Для водорода Е = е:

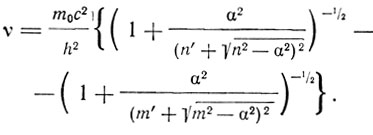
"тогда как по обычной механике энергии n + n' различных круговых и эллиптических орбит, относящихся к одному и тому же значению n + n', в точности совпадают, они, если принять во внимание переменную массу электрона, несколько различаются для этих n + n' орбит".

Мы бы сказали теперь, что релятивистская поправка снимает вырождение.

Развертывая выражение 1 + ^W/_m0c² по степеням малой величины а, Зоммерфельд получает выражение для

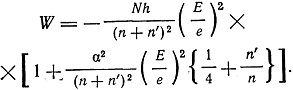
Таким образом, релятивистский эффект сказывается, с одной стороны, в повышении энергетического уровня в

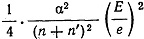
раз. Эту часть Зоммерфельд называет "релятивистской поправкой". С другой стороны, релятивистский эффект дает дополнительное повышение энергии, различное для различных эллипсов. Доля этого эффекта составляет величину

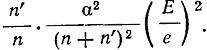
Эту часть Зоммерфельд назвал "расщеплением энергии". Все эти поправки определяются величиной α², которая, по Зоммерфельду, составляет около 5*10^-5. Далее Зоммерфельд дает более высокое приближение, учитывая члены с α².

Для видимого спектра эти уточнения излишни и можно ограничиваться разложением до α². В этом случае получаются следующие расщепления линий:

(n = 0 исключается как маятниковая .орбита). Этим двум значениям азимутального числа n соответствуют два уровня энергии: W_2,0, W_1,1. Разность этих уровней

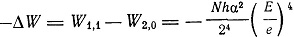
При переходе на эти уровни получается расщепление линий на две (дублеты). Разность частот дублета

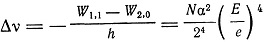
Для n + n' = 3 получаем триплеты соответственно трем способам разложения числа n + n' = 3, 3 = 3 + 0, 3 = 2 + 1, 3 = 1 + 2. Соответствующие значения энергии

будут W_3,0, W_2,1, W_1,2. При этом

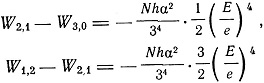
и разность частот компонент

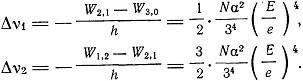
Так что Δv₁:Δv₂ = 1:3.

Для n + n' = 4 получается квартетное расщепление, причем Δv₁:Δv₂:Δv₃ = 1:2:6.

Для n + n' = 5 получаются квинтеты: Δv₁:Δv₂:Δv₃:Δv₄ = 3:5:10:30. Сериальный терм n + n' = 1 является простым. Он соответствует одной и только одной круговой орбите. Среди водородоподобных термов это единственный простой терм. Характер мультиплетности, соответствующий постоянному положительному терму, повторяется в каждой побочной серии. Главная серия соответствует переменному отрицательному терму и простому постоянному терму. Если же мультиплетность производится как положительным постоянным термом, так и отрицательным переменным, то характер картины тонкой структуры необычайно усложняется. Некоторые из вычисленных по формулам Зоммерфельда линий фактически не существуют, другие имеют малую, интенсивность. Аналогичные соотношения имеют место в водородоподобных спектрах, а именно тем точнее, чем более водородоподобный характер они носят.

Обсуждая вопрос о тонкой структуре водородных линий, Зоммерфельд указывает, что постоянный терм бальмеровской серии ¹/₂ дает начало дублетам с постоянной разностью частот Δv_H. Эта разность равна (E = e):

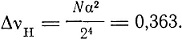
При этом α² принято равным 5,3*10^-5, N = 1,097*10⁵. По данным Майкельсона, для линий Δv = 0,32, для H_γ Δv = 0,42. Соответствующие значения разности длин волн Δλ, составляют соответственно Δλ_α = 0,14 А⁰.

Δλ_γ = 0,08 А⁰. По данным Фабри и Бюиссона, Δν_α = 0,307, Δν_γ = 0,132. Зоммерфельд считает наиболее приемлемыми эти последние.

На возникающий из постоянного терма дублет налагается мультиплет, возникающий из второго переменного терма. В случае линии На обе компоненты дуплета состоят из триплета, для линии Н_β из квартета, для Н_γ из квинтета и т. д. Зоммерфельд подробно разбирает все случаи расщепления водородных линий, расположение смещенных линий, соотношение их интенсивностей и т. д. Он приводит символические обозначения линий, данные Ф. Пашеном и С. А. Поповым в 1914 г. Согласно этим обозначениям частоты линий представляются в виде разностей термов (для 1-й побочной или диффузной серии):

где n, m - номера термов, i, j имеют значения (i≥j): i, j = 1, 2, 3 для триплетов, i, j = 1, 2 для дуплетов. Работа Пашена 1916 г., посвященная измерениям со спектром ионизированного гелия, подтвердила теорию Зоммерфельда. При этом измерения Пашена дали для Δv_H значения между 0,35 и 0,37. Зоммерфельд полагает из этих измерений для смещения

где Θ - положительная или отрицательная дробь. Отсюда

Зоммерфельд указывает, что тонкие спектроскопические измерения позволяют определить атомные константы m, e, h. Во-первых, предельное значение постоянной Ридберга N_∞ для бесконечно большой массы ядра дает возможность определить более точно одну из этих величин, если две известны:

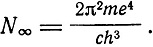
Далее, из значений

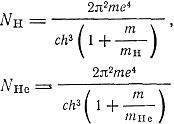
можно определить независимо ^e/_m, так как

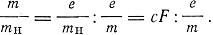
К этим уравнениям, данным Бором, Зоммерфельд добавляет уравнение для постоянной тонкой структуры

которая определяется из измерений водородного дублета либо гелиевого триплета. Тогда получаем три независимых уравнения (вместе с уравнениями Бора для N_H и N_He) для определения e, m, h.

Если к ним прибавить еще соотношения

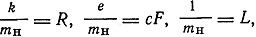
где k - постоянная Больцмана, F - число Фарадея, R - постоянная Клапейрона, L - число Лошмидта, то отсюда получаем и значения m_H, k, L. Однако возможность спектроскопического определения атомных величин появилась только после измерений Ф. Пашена, опубликованных в том же, 1916 г. в том же журнале, в каком появилась статья Зоммерфельда. Из его измерений а получалось

Далее он определял из своих измерений N_H и N_He, что приводило к значениям

Это приводит к значениям

Чтобы уменьшить неопределенность этих выражений, Зоммерфельд привлекает экспоненциальную константу в законе излучения, определенную в том же, 1916 г. Варбургом:

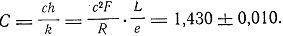
Зоммерфельд дает более широкое значение этой константы, введя правильную дробь η (положительную или отрицательную):

Сравнивая это значение С со значением, получаемым при подстановке предыдущих значений e и h (C = ¹/₄₁₆ + Θ*0,04), получим

Отсюда получается таблица значений:

Эти значения Зоммерфельд сравнивает со значениями, полученными Планком в его первой и второй статье, и со значениями Милликена, полученными в 1916 г.:

Планк I

Планк II

Милликен

Таким образом, значения Планка выпадают из пределов спектроскопических измерений, тогда как значения Милликена входят в них при η = ¹/₅. Зоммерфельд выражает уверенность, что последующие измерения уничтожат всякие сомнения в точности спектроскопических единиц.

"В нашей теории тонкой структуры,- писал он в своей книге "Строение атома и спектры",- слились вместе три главных направления современной теоретической физики: электронная теория, квантовая теория и теория относительности".

Другими словами, теория тонкой структуры имела не просто техническое значение уточнения деталей эксперимента, но и важное теоретическое значение. Но исследованием Зоммерфельда 1916 г. она еще не была завершена, оставались необъяснимые детали, не были сформулированы правила отбора. Следующий шаг в развитии теории был сделан уже Дираком.

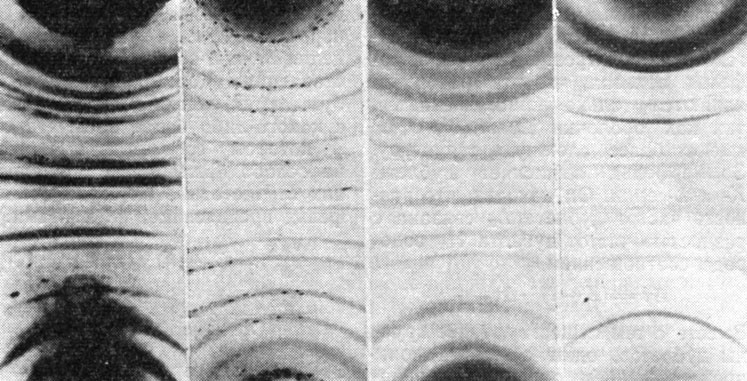
Рентгенограммы, полученные по методу Девая-Шеррера

Последняя, третья часть статьи Зоммерфельда посвящена теории рентгеновских спектров. Открытие Лауэ, Фридриха и Книпинга, с одной стороны, и У. Г. Брэгга и У. Л. Брэгга - с другой, привели к созданию спектрометра для рентгеновских лучей, в котором М. де Бройль заменил ионизационную камеру фотографической пластинкой. Мозли, В. Коссель (1914), М. Зигбан (1916) заложили основы рентгеноскопии, Дебай и Шерер в 1916 г. разработали дифракционный метод кристаллических порошков для исследования структуры кристаллов.

В результате этих исследований были изучены спектры серий К и L рентгеновских лучей, открыта серия М (Зигбан, 1916). Для частот линии K_α Мозли установил соотношение, которое можно записать в форме разности двух термов:

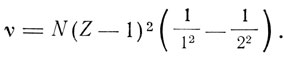
Таким образом, Мозли полагал, что линия Ка образуется при переходе электрона со второго кольца на первое. Он нашел также частоту линии K_β. Других линий серии К Мозли не нашел, зато нашел четыре линии серии L, которые обозначил символами L_α, L_β, L_φ, L_γ. Коссель в 1914 г. предположил, что между частотами линий К и L существует соотношение

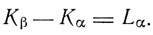
Коссель предполагает, что механизм возбуждения K-серии заключается в том, что электрон удаляется с самой внутренней оболочки (K-оболочки) на периферию атома. На освободившееся место перескакивает электрон из внешних слоев, излучая энергию. Линия K_α возбуждается при переходе электрона из L-оболочки на K-оболочку, линия K_β возбуждается при переходе электрона на K-оболочку из М-оболочки. Частота линии K_β больше, чем частота линии Ка, но интенсивность меньше. Зигбан нашел четыре линии серии К, которые обозначил соответственно α₁, α₂, β₁, β₂ в порядке возрастающих частот, Зоммерфельд ввел обозначения α', α, β, γ. Серия L получается аналогично при переходе электрона из внешних слоев М, N, ... на освободившееся место в слое L.

Зоммерфельд обозначает K-, L- и М-термы соответственно:

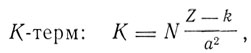
где Z - порядковое число, k = 1, a = 1, по Мозли.

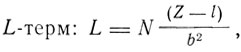
где l = 7,4, b = 2, по Мозли.

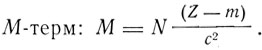
N - постоянная Ридберга.

При этом частоты колебаний получаются по схеме:

для K_α v = K - L,

для K_β v = K - M,

............................................

для L_α v = L - N.

............................................

В такой форме выглядит комбинационный принцип Ритца для рентгеновских спектров. Однако Зоммерфельд показал, что эти равенства являются только приближенными, так как оболочки L, M, N, О, Р имеют более сложную структуру. Зоммерфельд вычисляет дублеты K- и L-серии. Он находит, что разность частот дублета L_α связана с разностью частот дублета На водорода соотношением

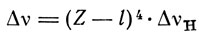
Вместе с тем существуют две группы дублетов, одни обязаны своим происхождением общему начальному уровню, но разным конечным, другие - общему конечному уровню, но разным начальным. В более поздних работах, когда Зоммерфельд обозначал подоболочки римскими индексами, он приводит таблицу дублетов, которую мы воспроизводим в измененном и сокращенном виде.

Важное место в исследовании Зоммерфельда занимает вопрос о возбуждении и поглощении рентгеновских лучей. Этому вопросу посвящен последний, восьмой параграф третьей части его статьи. Именно здесь он выражает сомнение в справедливости простого комбинационного правила Косселя ввиду сложной структуры электронных оболочек. Здесь он анализирует связь между границей поглощения рентгеновских лучей, открытой Е. Вагнером в 1915 г., и границей возбуждения K- и L-серии. Согласно представлениям Косселя эти серии возбуждаются, когда электрон падает с какого-либо более внешнего слоя А, которому соответствует номер X на освободившееся место в слое K или L. Частоты этих серий Зоммерфельд представляет формулами:

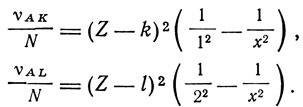
Зоммерфельд представляет, что номер х измеряет протяженность невозмущенного кулонового поля. Поскольку х>2, термы K и L, соответствующие боровским номерам 1 и 2, находятся целиком внутри кулоновой области и являются водородоподобными. Более высокий терм, соответствующий числу 3, возмущен действием электронного облачка ("электронной сферы", по терминологии Зоммерфельда), и поэтому М-, N-, О-, Р-термы не водородоподобны. Радиус электронной сферы имеет порядок атомного радиуса, точнее, несколько меньше атомного радиуса. В отличие от атомного радиуса, который испытывает периодические изменения, радиус внутренней или "средней" электронной сферы R постепенно убывает с возрастанием порядкового номера, что объясняется увеличением притяжения заряда ядра. Никакой периодичности радиуса R не замечается.

Зоммерфельд подчеркивает далее, что различие между оптическими и рентгеновскими спектрами заключается в том, что оптические спектры возбуждаются периферическими электронами, не принадлежащими к электронному облаку, тогда как рентгеновские спектры испускаются внутри этого облака. Как оптические, так и рентгеновские спектры будут тем более водородоподобными, чем дальше от электронного облака расположено место их возбуждения. Поэтому в видимых спектрах простота сериального закона сохраняется тем лучше, чем выше сериальный номер, в рентгеновских же спектрах, наоборот, только для наиболее низких чисел 1 и 2 (серии K и L); для высших номеров орбиты проникают в электронное облако и, чем более это проникновение, тем сложнее сериальный закон.

Далее, в оптических спектрах сериальный терм является одновременно границей спектра испускания данной серии. Наоборот, в рентгеновских спектрах сериальный терм отличен от границы спектра испускания, а граница спектра испускания совпадает с границей поглощения, обнаруженной Вагнером. Поэтому, указывает Зоммерфельд, измерение поглощения имеет важное значение для понимания процессов излучения и для структуры боровской модели.

"Главным результатом нашей теории в ее применении к рентгеновским спектрам,- заключает Зоммерфельд свою статью,- является сведение L дублетов к водородным дублетам... к выделению L-терма присоединилось выделение К-, М-, N-, О-, Р-термов. То, что при этом K- и L-термы,_а не следующие М-, N- ;:. термы оказались водородоподобными, является весьма удовлетворительным и указывает на то, что в более периферических частях атома - месте, в котором разыгрываются процессы М-, N- ... термов, соотношения оказываются менее простыми, чем в центральных частях, где проходят К- и L-орбиты. Менее удовлетворительными являются дробные и частью отрицательные характеристики ядерного заряда, к которым приводит наше вычисление; то, что при этом относящиеся к К- и L-термам числа k и l оказываются совершенно независящими от порядкового номера (а именно, вплоть до наименьших значений Z, для которых еще имеются наблюдения), является опять-таки весьма замечательным для этой модели; отсюда можно заключить что внутреннее строение атома для всех Z, вне определенной границы в основном оказывается одинаковым. Замечательно также, что до сих пор еще не обнаружилось в области рентгеновских спектров никакого указания на "периодическую систему элементов". Очевидно, только внешние части атомов, в которых разыгрываются оптические и химические процессы, имеют периодическую природу; внутренние же части, в которых происходят те электронные движения, которые приводят к испусканию и поглощению рентгеновских лучей, являются, напротив, совершенно однородными и определяются линейно-возрастающим образом через порядковый номер элемента".

Чтобы покончить здесь с вопросом о рентгеновских лучах, укажем,, что в 1915 г. Дюан и Хант установили закон, определяющий коротковолновую границу непрерывного спектра. Этот закон гласит, что предельная длина волны, соответствующая коротковолновой границе, измеряется с напряжением в трубке таким образом, что произведение длины волны λ_min на напряжение V остается постоянным:

Существование этой границы было теоретически предсказано Эйнштейном еще в 1909 г. Закон Дюана и Ханта был подтвержден многочисленными исследованиями Е. Вагнера, Хэлла, Хэлла и Раиса, Вебстера и др. Эти исследования не только подтвердили справедливость закона,, но и дали возможность нового определения константы h. Поскольку этот закон естественно вытекает из теории фотоэффекта Эйнштейна:

если λ выражено в ангстремах, а V в вольтах, Вагнер из своих измерений нашел h = 6,52*10^-27, Мюллер h = 6,57*10^-27 (измерения выполнены в 1916 г.). Так квантовая теория нашла новое подтверждение.

Оценивая закон Дюана-Ханта, известный немецкий физик В. Герлах писал: "Закон Дюана-Ханта замечателен, с одной стороны, тем, что он в количественном отношении соответствует балансу энергии Эйнштейна eV = hv и тем самым предоставляет этому фундаментальному квантовому правилу принципиальную роль в теории непрерывного рентгеновского спектра, с другой стороны, тем, что он по своему смыслу соответствует закону смещения Вина для теплового спектра".