Световые кванты Эйнштейна

Закон В. Вина, с которого Эренфест начал разработку адиабатической гипотезы, появился и в новом замечательном исследовании Эйнштейна о световых квантах, напечатанном в "Трудах немецкого физического общества" в 1916 г. и в журнале "Physikalische Zeitschrift" в 1917 г. Обратимся к рассмотрению этой последней работы.

В. Вин

Статья Эйнштейна 1917 г. носит название "К квантовой теории излучения". Она начинается с указания на замечательное сходство кривых максвелловского распределения скоростей и распределения энергии черного излучения по частотам. Эйнштейн обращает внимание на то, что именно эта аналогия привела Вина к его выводу формулы

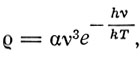
хорошо соответствующей опыту в области высоких частот. Эйнштейн замечает, что формула Планка

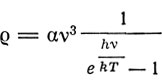
заставила забыть и формулу Вина. Он сообщает далее, что в статье 1916 г. им был найден вывод формулы Планка, схожей с первоначальным виновским выводом своей формулы. Рассуждения этой статьи Эйнштейн повторяет и в обсуждаемой нами статье. Вывод Эйнштейном формулы Планка, как он указывает, "базируется на основном предположении квантовой теории, в котором выявляется соотношение между максвелловской кривой и кривой хроматического распределения". "Этот вывод,- продолжает Эйнштейн,- заслуживает внимания не только вследствие своей простоты, но и особенно потому, что он, как кажется, вносит некоторую ясность в столь еще темный для нас процесс испускания и поглощения материей излучения".

Основная идея эйнштейновского вывода заключается в том, что молекулы материи находятся в температурном равновесии с планковским излучением благодаря процессам испускания и поглощения излучения. "Если введенные гипотезы о взаимодействии излучения и материи верны,- пишет Эйнштейн,- то они должны давать больше, чем правильное статистическое распределение внутренней энергии молекул. А именно, при поглощении и испускании излучения происходит также передача импульса молекулам, а это приводит к тому, что посредством одного взаимодействия излучения и молекул устанавливается определенное распределение скоростей молекул". Эйнштейн полагает, что это распределение должно быть тождественно с распределением, устанавливаемым благодаря взаимным столкновениям молекул, т. е. должно быть тождественно с максвелловским распределением. Это приводит к требованию, что средняя кинетическая энергия, приходящаяся на одну степень свободы молекулы, находящейся в поле планковского излучения, должна равняться ¹/₂kT, независимо от природы молекулы и испускаемых и поглощаемых ею частот. "В этой статье мы докажем, что это далеко идущее требование действительно удовлетворяется самым общим образом, тем самым наша простая гипотеза об элементарных процессах испускания и поглощения получает новую опору". В связи с этим Эйнштейн ставит вопрос: испытывает ли молекула отдачу, когда она излучает энергию ε? С точки зрения классической электродинамики при излучении энергии ε тело испытывает отдачу, соответствующую импульсу ^ε/_c. Но если излучение осуществляется волной, симметрично расходящейся во все стороны, то отдачи не происходит, она происходит только тогда, когда излучение ε локализовано в определенном направлении. "Оказывается,- подчеркивает Эйнштейн,- что мы тогда приходим к непротиворечивой теории, когда представляем такой элементарный процесс (испускания или поглощения излучения. - П. К.) полностью направленным. В этом состоит главный результат последующих рассуждений".

Таким образом, Эйнштейн в своей знаменитой статье становится на точку зрения "игольчатого излучения", локализованного в определенных направлениях. Кванту такого излучения, обладающему энергией ε, соответствует импульс ^ε/_с. Это материальное образование получило позже название "фотон" (1923. А. Комптон).

Далее Эйнштейн принимает гипотезу Бора, что молекула, если отвлечься от ее ориентации и поступательного движения, может принимать только дискретные состояния Z₁, Z₂, ..., Z_n, ..., в которых она обладает энергией ε₁, ε₂, ... , ε_n, ... Если эти молекулы являются молекулами газа, то относительная частота W_n состояния Z_n определяется формулой Больцмана

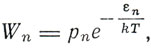
где p_n - статистический "вес" состояния Z_n. Этот закон Эйнштейн называет "далеко идущим обобщением закона распределения скоростей Максвелла". Он подчеркивает, что последние принципиальные успехи квантовой теории связаны с теоретическим определением возможных квантовых состояний и их весов p_n.

Далее Эйнштейн переходит к своим знаменитым гипотезам об обмене энергией излучением. Он рассматривает два квантовых состояния Z_n и Z_m, энергии которых удовлетворяют неравенству ε_m>ε_n. Молекула переходит из состояния Z_n в состояние Z_m, поглотив избыточную энергию ε_m-ε_n. При обратном переходе Z_m→Z_n она отдает эту избыточную энергию. Частота этой испускаемой или поглощаемой энергии имеет величину v, характерную для данной комбинации индексов (m, n). Затем Эйнштейн переходит к гипотезам, относящимся к переходу (m, n).

1. Гипотеза испускания. Молекула может перейти из состояния Z_m в состояние Z_n спонтанно, не понуждаемая внешними причинами. При этом она испускает энергию ε_m - ε_n в виде излучения с частотой v. Вероятность dW того, что этот переход действительно произойдет за промежуток времени dt, по Эйнштейну, определяется уравнением

где A_mⁿ означает характерную для данной комбинации индексов (m, n) константу.

2. Гипотеза об облучении(Einstrahlung). Гипотеза об облучении Эйнштейна заключается в том, что молекула, находящаяся в поле излучения с объемной плотностью ρ, может под действием этого поля перейти из состояния Z_n в состояние Z_m, поглотив из поля необходимую для перехода энергию ε_m - ε_n. Вероятность такого перехода за время dt определяется уравнением

dW = B_n^mdt, (B)

Но под действием поля возможен и обратный переход (этот переход позже получил название "индуцированное излучение"), сопровождающийся излучением энергии Z_m→Z_n, согласно вероятностному закону

dW = B_mⁿdt, (B)

где B_n^m и B_mⁿ - характеристические константы. Оба эти процесса Эйнштейн назвал "изменением состояния посредством облучения". Процесс (B') в наше время получил важное значение, поскольку на нем основано действие квантовых генераторов света - лазеров. Эйнштейн указывает далее, что процессы обмена энергией между молекулой и излучением сопровождаются передачей импульса. Если направленный пучок излучения передает молекуле энергию ε_m - ε_n, то вместе с этим он передает и импульс ^{ε_m - ε_n}/_c. Эйнштейн предполагает, что при одновременном действии нескольких пучков энергия ε_m - ε_n и соответствующий импульс ^{ε_m - ε_n}/_c передаются молекуле в элементарном процессе от одного пучка. При излучении молекула отдает энергию ε_m - ε_n и импульс ^{ε_m - ε_n}/_c. Если молекула изотропна, то все направления излучения равновероятны. Для неизотропных молекул получится то же самое, если ориентация молекулы будет меняться со временем по закону случая. Это необходимо принять, так как иначе коэффициенты B_n^m и B_mⁿ зависели бы от направления. Эта зависимость устраняется допущением изотропности молекулы или ее средней по времени изотропности. Эйнштейн переходит затем к выводу формулы Планка, в основе которого лежит допущение, что процессы обмена энергией между молекулой и излучением не нарушают закона распределения состояний:

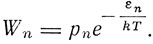
"Для этого необходимо и достаточно, чтобы в среднем в единицу времени происходило бы столько же элементарных процессов типа (В), как и типа (А) и (В') вместе". Отсюда для элементарных процессов, соответствующих комбинациям индексов (m, n), получается уравнение

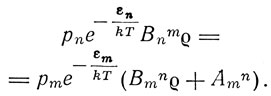
Полагая, что при T→∞, →∞, получаем

и, следовательно,

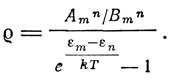
Далее, из закона смещения Вина

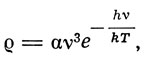
справедливого для высоких частот, следует

где α и h - универсальные константы. Для определения а надо иметь точную теорию электродинамических и механических процессов. Эйнштейн указывает на предельный случай высоких температур Рэлея, когда справедлива классическая теория. Уравнение

представляет условие Бора, "о котором, по Зоммерфельду и Эпштейну, уже можно утверждать, что оно принадлежит к прочным достижениям нашей науки. Оно содержит в скрытом виде, как я показал, также закон фотохимической эквивалентности". Ныне замечательный вывод формулы Планка Эйнштейном вошел во все учебники. Правда, сегодня уже при ее выводе не вспоминают о законе Вина и, опираясь на принцип соответствия, которого Эйнштейн еще не знал, определяют константы уравнения равновесия из закона Рэлея-Джинса. На этот способ определения констант, как мы видели, указал еще Эйнштейн. Еще раз подчеркиваем, что на идею индуцированного излучения обратили внимание почти полвека спустя, в период становления квантовой радиофизики.

Последняя часть статьи Эйнштейна посвящена механическому поведению молекул в поле излучения. Здесь характерна аналогия, проводимая Эйнштейном, между этим поведением и поведением броуновской частицы в среде. Таким образом, Эйнштейн рассматривает флюктуации излучения, вследствие которых молекула в поле излучения будет получать нерегулярные толчки. Другим влиянием излучения на движение молекул будет испытываемое молекулой сопротивление движению, пропорциональное скорости - Rv, где R - некоторая константа "трения", обусловленного излучением. Рассматривая линейное движение молекулы вдоль оси х, Эйнштейн пишет, что по истечении короткого промежутка времени τ импульс молекулы будет

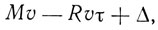
где Δ - импульс, сообщаемый молекуле в течение времени τ вследствие флюктуации излучения. Учитывая, что распределение скоростей молекул носит стационарный характер, Эйнштейн пишет

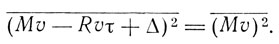
Полагая υ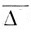 равным нулю, Эйнштейн находит

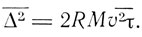
При тепловом равновесии для линейного движения

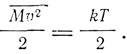
Поэтому

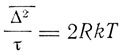
закон, аналогичный закону, найденному Эйнштейном для броуновского движения. Но 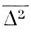и R подлежат дальнейшему определению из эйнштейновских гипотез о взаимодействии между частицей и излучением. Если вставить результаты этих вычислений в написанное уравнение, то оно будет удовлетворяться тождественно, если ρ(υ, T) выразить из формулы Планка. Вычисления, приведенные Эйнштейном, дают для R выражение

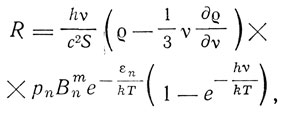
где

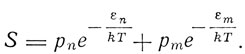
"Значительно проще,- пишет Эйнштейн,- рассчитать действие нерегулярностей элементарных процессов на механическое поведение молекулы". Пусть молекулам в направлении х вследствие нерегулярностей сообщаются независимые импульсы λ₁, λ₂, ... . Тогда сообщаемый в целом в течение τ импульс

Так как вследствие нерегулярностей направлений и величин отдельных импульсов λ_υ среднее значение λ_υ = 0, то вычисляем средний квадрат импульса

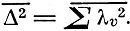
Если одинаковы и равны , причем число импульсов равно l, то

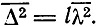
Но импульс, сообщаемый молекуле, при излучении или облучении

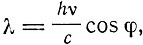
где φ - угол между осью х и случайным направлением. Поэтому

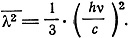
Далее l определяется как

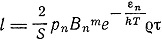
и

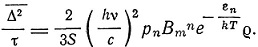
Основной гипотезой в этих вычислениях Эйнштейна является гипотеза, что импульсы, сообщаемые молекуле излучением, не нарушают термодинамического равновесия.

Обсуждая итоги своей работы, Эйнштейн пишет о своих гипотезах о взаимодействии между частицей и излучением, что он был приведен к ним "стремлением постулировать возможно более простым образом квантовотеоретическое поведение молекул". Он указывает, что из его гипотез естественно получается постулат Бора и формула Планка. "Но наиболее важным,- пишет Эйнштейн,- мне кажется результат в отношении импульса, переносимого на молекулу при облучении и излучении".

При получении или отдаче энергии в форме излучения энергии hv она получает импульс ^hv/_с при поглощении энергии в направлении распространения пучка излучения, при излучении в противоположном направлении. Процессы поглощения и испускания излучения являются направленными. "Молекула испытывает в элементарном процессе излучения отдачу величиной ^hv/_с в направлении, которое при теперешнем состоянии теории определяется только "случаем".

Эта удивительно наглядная механическая картина взаимодействия частицы с излучением, по Эйнштейну, еще не полна. Пока направление излучения определяется только законами случая. Поэтому Эйнштейн следующим образом характеризует недостатки своей теории: "Слабость теории заключается, с одной стороны, в том, что она не приводит нас к более тесному контакту с волновой теорией, а с другой стороны, в том, что она предоставляет время и направление элементарного процесса "случаю ..." "Несмотря на это, - добавляет Эйнштейн, я питаю полное доверие к надежности избранного пути".

Характерно для мировоззрения Эйнштейна недоверие к статистическим законам. "Я не верю в бога, играющего в кости",- писал он М. Борну. Это "неверие в бога, играющего в кости" проявилось и здесь при формулировке Эйнштейном недостатков своей теории. Вместе с тем он сохраняет полную уверенность в ее надежности, и эта уверенность оправдалась: основные черты теории Эйнштейна полностью сохранились в современных представлениях, а его идея передачи импульса частице блестяще подтвердилась в открытом в 1922 г. А. Комптоном эффекте. А именно, Эйнштейн неустанно подчеркивал в своей статье и еще раз в ее конце, что "для теоретического рассмотрения передача импульса, несмотря на ее незначительность, должна рассматриваться как равнозначная с бросающейся в глаза передачей энергии, поскольку энергия и импульс самым тесным образом связаны друг с другом". И это утверждение Эйнштейна принадлежит к прочим завоеваниям современной физики. Оно было подтверждено многочисленными фактами, начиная с эффекта Комптона и кончая эффектом Мёссбауэра. Эйнштейн опирался только на свою огромную физическую интуицию и на тот факт, что в его теории учет передачи импульса излучением приводит "к таким движениям, какие требует теория теплоты".

Подводя итоги, мы можем сказать, что в военные годы не прекращалась теоретическая работа, углубляющая революцию в физике. Работы по теории атома Бора, Зоммерфельда, Эпштейна, Шварцшильда, Дебая, Эренфеста, работы по теории относительности и теории квантов Эйнштейна, работы по спектроскопии рентгеновских лучей У. Л. и У. Г. Брэггов, Мозли, Косселя, Зигбана расширяли и углубляли брешь, пробитую в здании классической физики новыми открытиями и теориями. Послевоенная физика развернулась с самого начала как физика атома по преимуществу. Развитие новой квантовой механики, замечательные успехи ядерной физики были подготовлены всем предыдущим довоенным и военным развитием физики. Период 1901 - 1918 гг. был также периодом подготовки советской физики, превратившейся в наше время в передовой отряд мировой науки.