Обзор успехов теории Бора в 1918-1923 годах

В 1929 г. Гейзенберг выступил со статьей о развитии квантовой теории в 1918-1928 гг. Период 1918-1923 гг. он называл периодом успехов старой квантовой теории Бора. Среди этих успехов он отмечает теорию тонкой структуры спектральных линий Зоммерфельда, введение Шредингером идеи "проникающих" орбит, формальное истолкование Зоммерфельдом спектров щелочных металлов и дублетных и триплетных структур путем введения внутреннего квантового числа.

"Наиболее убедительным доказательством правильности пути, пройденного теорией,- пишет далее Гейзенберг,- было открытое Бором истолкование периодической системы с помощью квантовой гипотезы. Характерным для боровских исследований было то, что Бор применял идеи классической механики только качественно, только постольку, поскольку их применимость в квантовой физике могла быть подтверждена принципом соответствия. Только такая свобода по отношению к классическим идеям - или лучше: по отношению к тем следствиям классических идей, которые противоречат принципам квантовой теории,- сделала возможной качественную связь химических и спектральных свойств атома". Вместе с тем Гейзенберг отмечает и успехи, достигнутые в количественном объяснении спектров теорией Бора. При этом область применимости классической механики в квантовой теории ограничивалась адиабатической гипотезой Эренфеста. В юбилейном номере "Naturwissenschaften", посвященном 10-летию теории Бора, П. С. Эренфест выступил со статьей "Адиабатические преобразования в теории квантов и их трактовка Бором". Поставив целью этой статьи "показать в более генетическом изложении", как постепенно в квантовой статистике вводилась адиабатическая гипотеза, как выдвигалось понятие "адиабатических инвариантов" и как пришли к "теореме адиабатических инвариантов априорных весов", Эренфест в заключение указывал на те места в сочинениях Бора, в которых особенно отчетливо выступает адиабатическая гипотеза и которым мы обязаны выяснением и углублением этой гипотезы и открытием совершенно новых перспектив. Сочинения Бора, на которые ссылается Эренфест, это: "О квантовой теории линейчатых спектров", сборник статей Бора 1918-1922 гг., изданный Копенгагенской академией в 1922 г., немецкий перевод которого вышел в 1923 г., статья "Основные постулаты квантовой теории", опубликованная в "Zeitschrift fur Physik" за 1923 г., сборник статей по теории атома 1921 г. и особенно статья 1916 г. о применении теории квантов к периодической системе, а также предисловие к этому сборнику. Бор подчеркивает, что принцип соответствия и адиабатическая гипотеза не означают "примирения" квантовой теории с классической, и показывал, что они, несмотря на их "квазиклассическую" формулировку, должны рассматриваться как "чисто квантовотеоретические принципы". Он выяснил связь между адиабатическим принципом и принципом соответствия. Еще в статье 1913 г. Бор использовал медленный адиабатический процесс сближения двух нейтральных атомов водорода для образования молекулы водорода. В статье 1916 г. о применении квантовой теории к периодической системе, которая была опубликована только в сборнике 1921 г. Бор использовал установленный Эренфестом адиабатический инвариант для рассмотрения ряда весьма интересных вопросов. Он рассмотрел случаи вырождения атомов с помощью теории адиабатических преобразований и Эренфест называет исследования Бора о многократно периодических системах наиболее глубокими и красивейшими из всего, что до сих пор известно вообще об основах квантовой теории.

Среди успехов квантовой теории, относящихся к периоду 1918-1923 гг., Гейзенберг называет исследования Пашена и Бака по эффекту Зеемана в сложных атомах и формальное описание экспериментальных результатов в области аномального эффекта Зеемана с помощью формулы Ланде. Мы уже упоминали об этих результатах и теперь остановимся на них несколько подробнее.

Описание спектров в сложных атомах, в первую очередь в атомах щелочных металлов, с помощью модели Бора было начато как самим Бором, так и Д. С. Рождественским. Оба автора независимо друг от друга пришли к идее оптического (излучающего) электрона выделяемого из всей группы электронов атома. Д. С. Рождественский впервые указал на водородоподобный характер отдаленных орбит. Разделение термов на водородоподобные и неводородоподобные обусловлено характером орбиты. Чем дальше проходит орбита от ядра и остальных электронов, тем более водородоподобными являются термы, соответствующие этим орбитам. Рождественский, по существу, впервые указал на различие проникающих и непроникающих орбит, которое было проведено позднее Шредингером в 1921 г. Следует отметить, что в этот период спектроскописты произвели большую и сложную работу по интерпретации спектров и расшифровке спектральных термов. Как мы уже знаем, Ридберг ввел для бальмеровских термов поправку так, что терм принимает вид ^R/_(m+μ)², Ритц ввел вторую поправку, и терм с поправкой Ритца имеет вид ^R/_{[m + a + α(m,a)]²}. Поправка а у различных авторов обозначалась по-разному, Хвольсон в своем дополнительном томе курса физики дает табличку обозначений современных ему авторов

Частоты спектральных линий в соответствующих сериях изображались в соответствии с обозначениями, предложенными Пашеном

Для третьего издания своей книги Зоммерфельд вместо f, g, h использовал обозначения b, x, y.

Происхождение поправок Ридберга-Ритца Зомерфельд объяснял наличием возмущений, оказываемых на оптический электрон остальными электронами оболочки. В первом приближении, когда потенциал чисто кулоновский 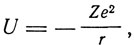получаются водородоподобные термы вида 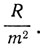. Во втором приближении, когда 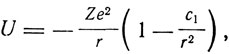получается поправка Ридберга и термы вида 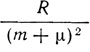и в третьем приближении 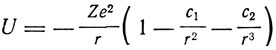получается поправка Ритца и термы вида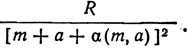

Шредингер объяснил поправки наличием проникающих орбит. Для оценки термов он заменил действие электронного остова сферической оболочкой, равномерно заряженной отрицательно. Во внешнем поле эта оболочка действует как заряд Z^α, равный 1 для нейтрального атома, 2 для ионизированного атома и т. д. Внутри также получается кулоновское поле, но соответствующее более высокому заряду Z⁽ⁱ⁾. Вычисленная в этих предположениях поправка Ридберга а, оказалась отрицатель, ной и мало зависящей от т. Она тем больше, чем больше радиус оболочки и чем больше Z⁽ⁱ⁾. Бор (1922) установил, что для проникающих орбит при данном k поправка Ридберга незначительно отличается от разности между главным квантовым числом и орбитальным, уменьшенным на 1.

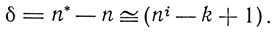
Здесь n^* - эффективное квантовое число:

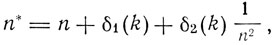
где δ₁ - поправка Ридберга, δ₂ - поправка Ритца; nⁱ - значение радиального квантового числа для наибольшей проникающей орбиты, целиком лежащей в остове. М. Борн и В. Гейзенберг (1924) рассчитали поправки δ₁ и δ₂ методом теории возмущений, полагая потенциальную энергию равной

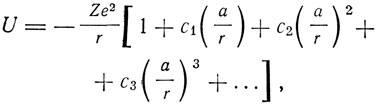
где а - длина порядка атомного радиуса. При этом

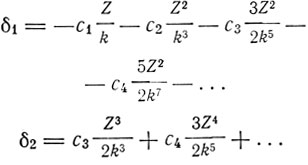
Одной из причин возмущения кулоновского поля Борн и Гейзенберг считали поляризацию электронного ?остова, обусловленную действием поля оптического электрона.

Поле оптического электрона ^e/_r² можно считать на протяжении остова постоянным, поскольку r велико. Момент, индуктируемый в остове, p = αE = α^e/_r². Сила, производимая диполем с этим моментом на электрон, равна ^2pe/_r³ = ^2αe2/_r⁵, чему соответствует потенциал -^αe3/_2r⁴. Если считать, что все остальные возмущения ничтожны, то поправки, обусловленные поляризацией, будут

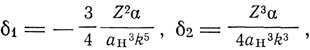
здесь а_н - радиус одноквантовой орбиты в атоме водорода. Вычисление из эмпирически найденных поправок Ридберга-Ритца поляризуемости а дает значения того же порядка, как и значения поляризуемости, определенной из измерений физической постоянной инертных газов. Таким образом, конфигурация электронного остова щелочных металлов оказывается аналогичной конфигурации инертных газов, что является подтверждением боровской теории периодической системы. Но при этом для удовлетворительного количественного совпадения следует ввести дробное значение квантового числа к. Установив этот факт, М. Борн пишет в своих "'Лекциях по атомной механике": "Нужно ожидать, что при дальнейшем развитии теории собственные квантовые величины останутся, как и до ?сих пор, целыми числами и что величина k, встречающаяся в нашей приближенной теории, не представляет собой такой квантовой величины, а каким-то непосредственным образом состоит сама из них". Однако последующее развитие квантовой механики не оправдало ожиданий Борна, дело оказалось сложнее, чем он думал.

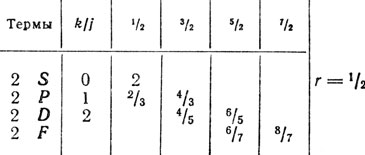
Еще в 1919 г. А. Ланде установил, что оптический электрон в атоме щелочных металлов совершает движение с тремя степенями свободы. Это возможно только в том случае, если момент количества движения оптического электрона, соответствующий его орбитальному движению, не совпадает по направлению с полным вращательным импульсом атома. Следовательно, атом имеет какой-то дополнительный вращательный импульс. Этот импульс Ланде приписал остову атома, т. е. ядру и остальным электронам. Орбита оптического электрона должна совершать медленную прецессию вокруг полного вращательного импульса агома, равного геометрической сумме орбитального импульса K и импульса остова R. При этом оба слагаемых импульса квантуются: K = k^h/_2π, R = r^h/_2π. Следовательно, должен квантоваться и полный импульс j = j^h/_2π. В 1920 г. Зоммерфельд в поисках описания сложных термов (дублетов и триплетов) атомов ввел новое квантовое число, названное им "внутренним квантовым числом". Это внутреннее квантовое число j определяло полный момент атома J. Оно может изменяться только в соответствии с правилом отбора Δj = 0, ±1, тогда как орбитальное квантовое число меняется только на 1 (Δk = ±1). С помощью внутреннего квантового числа j Зоммерфельд описал мультиплетный характер термов сложных атомов. Термы s (k = 1) оказываются простыми, термы p, d, f ... щелочных металлов оказываются двойными, каждому из которых соответствует полуцелое число j. Значение г оказывается, таким образом, равным ¹/₂. j = k ± ¹/₂. Таблица термов щелочных металлов имеет вид:

Величину расщепления для термов с орбитальным квантовым числом k Ланде нашел в виде

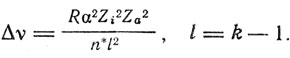
В 1921 г. Ланде, развивая свою векторную модель атома, формально описал аномальный эффект Зеемана. Для слабых магнитных полей он получил правильное описание эффекта, введя числовой множитель, который получил название множителя Ланде:

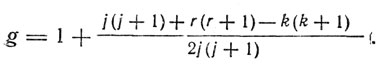
Отсюда для дублетов щелочных металлов получаются значения:

Энергия, соответствующая терму n, k, j, приобретает в магнитном поле значение

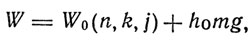
где 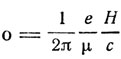частота прецессии Лармора, m = j, j-1, ..., 0, -1, ..., -(j-1), -j - магнитное квантовое число, определяющее компоненту полного вращательного импульса в направлении поля. Здесь начинают играть существенную роль исследования швейцарского физика Вольфганга Паули.

Н. Бор и В. Паули

В. Паули не считал обоснованной конфигурацию замкнутой системы электронов, предложенную Бором. В нобелевской речи он вспоминает, что на него произвело сильное впечатление то, "что Бор тогда и в последующих дискуссиях говорил об общем правиле, по которому происходило бы заполнение любой оболочки и в котором, в противоположность попытке Зоммерфельда, число 2 было бы столь же существенным, как и 8".

По приглашению Бора Паули приехал осенью в Копенгаген и там занялся аномальным эффектом Зеемана. В 1946 г. Паули вспоминал об этом в шутливой форме. Он говорил: "Аномальный тип расщепления был особенно интересен тем, что хотя он и подчинялся красивым и простым законам, однако понять его было очень трудно, так как самые общие предположения об электроне, исходящие как из классической, так и из квантовой теории, приводили всегда к одному и тому же триплету. При более близком знакомстве задача казалась мне еще более недоступной. Коллега, встретивший меня, когда я бесцельно бродил по прекрасным улицам Копенгагена, дружески сказал: "Вы выглядите очень несчастным". На что я пылко ответил: "Как может человек выглядеть счастливым, если он думает об аномальном эффекте Зеемана?" Для описания эффекта Зеемана, как мы знаем, Ланде пришлось ввести векторную модель атома, приписать остову атома вращательный момент 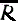, который, складываясь геометрически с орбитальным моментом оптического электрона 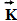, давал полный момент атома 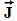. При этом появились для квантовых чисел дробные значения. Чтобы избежать дробных значений, Зоммерфельд и другие прибавляли к внутреннему квантовому числу j половину. Позже были введены обозначения S для квантового числа, характеризующего проекцию R на направление магнитного поля, L - для квантового числа, характеризующего проекцию вектора орбитального момента 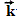на ось поля, и J для проекции 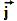. Число L принимало значения 0, 1, 2, 3 ..., которым соответствовали обозначения термов S, Р, D, F... Число S принимало значения 0, ₁/₂, 1, ₃/₂, ... . Число J принимало значения L + S, L + S-1, ..., L - S, если L≥S, и S + L, S + L - 1, ..., S - L, если L<S. Мультиплетность спектральной линии определялась числом 2S + 1. Для щелочных металлов S = ₁/₂ и мультиплетность равнялась 2. Для триплетов S = 0, ±1 ... В магнитном поле каждый терм расщепляется на 2J + 1 компоненты, различающиеся значениями магнитного числа М = J, J-1, ..., -J. Дополнительная энергия расщепленного терма

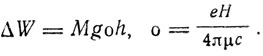
Множитель Ланде

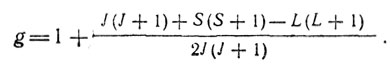
Отношение между магнитным моментом остова и его вращательным моментом оказалось аномальным, а именно вдвое больше нормального. Соответствующая ему добавочная энергия

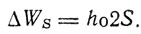
Этот "двойной магнетизм" вектора 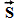является существенной основой аномального эффекта Зеемана и вместе с тем, если он действительно соответствует атомному остову, находится в противоречии с представлением о магнитном действии движущихся зарядов. Противоречие состоит также и в том, что атомный остов щелочных металлов соответствует конфигурации благородных газов, которая обладает замкнутым характером и не должна обладать вращательным суммарным моментом и соответственно магнитным моментом.

В своем обзоре "Успехи в исследовании эффекта Зеемана", опубликованном в 1923 г. Альфред Ланде замечает, что дробные значения фактора для аномального эффекта Зеемана говорят о "несостоятельности классической механики и электродинамики в большей степени, чем постулировала до сих пор квантовая теория". Аномальный эффект Зеемана, по мнению Ланде, указывает на необходимость модификации квантовой теории, которая должна дать "глубочайшие выводы о механизме строения атома".

"При этом, добавляет Ланде,- все признаки указывают на то, что окончательное решение этих вопросов в принципе уже на пороге". (Курсив мой.- П. К.).

Такого решения ожидает не только аномальный эффект Зеемана, но и магнитооптические опыты Эйнштейна и де Гааза, Барнета и их последователей, в которых получалось аномальное отклонение равное 2 между ожидаемым и фактически получившимся магнитным моментом вращающихся масс.

Ланде чувствует, что его формальная модель требует нового физического обоснования, которого, по его мнению, осталось ждать недолго.

И действительно, не прошло и двух лет после опубликования обзора Ланде, как в физику вошла идея спина.

Ланде в своем обзоре отмечает только что появившуюся статью Паули, которую он называет "важным шагом в формальном описании эффекта Пашена-Бака".

Эта статья поступила в редакцию журнала "Zeitschrift fur Physick" в апреле 1923 г. Паули исследовал расщепление в сильных магнитных полях. В сильных магнитных полях взаимодействие моментов L и S становится слабым по сравнению с действием магнитного поля на каждый момент в отдельности (эффект Пашена - Бака). Вклад орбитального магнитного момента в добавочную энергию составит о. h. M_L, вклад момента остова о. h. 2M_s, так что расщепление будет определяться добавочной энергией

Паули составил таблицу расщеплений в единицах нормального расщепления. В соединении с правилом отбора эта таблица объясняет, почему в сильных полях эффект Зеемана получается нормальным. Паули далее находит правило сумм: если составить сумму расщеплений всех термов с одним и тем же М, но разными J, возникающих из одного и того же дублета, как для слабого поля (∑_jMg), так и для сильного поля (∑_j(M_L+2M_s), то обе суммы оказываются одинаковыми. Пользуясь этим правилом, Паули определил набор множителей Ланде. В нобелевской лекпии об этой своей работе Паули говорил: "... мне удалось обобщить анализ термов, проделанный Ланде. на случай очень сильных магнитных полей,- случай, который из-за магнитооптического перехода во многих отношениях проще (эффект Пашена-Бака). Эта ранняя работа имела решающее значение для открытия принципа запрета".

Паули продолжает: "Очень скоро после возвращения в 1923 г. в Гамбургский университет в качестве приват-доцента я прочитал вступительную лекцию о периодической системе элементов. Содержание этой лекции совсем не удовлетворило меня, так как проблема заполнения электронных оболочек тогда не продвинулась еще ни на шаг. Единственное, что было ясно,- это то, что между этой проблемой и теорией мультиплетной структуры должна существовать теснейшая связь. Поэтому я предпринял попытку еще раз рассмотреть простейший случай - дублетную структуру щелочных металлов. Согласно ортодоксальной в то время точке зрения, которой придерживался и Бор в своих уже упомянутых геттингенских лекциях, причиной этой дублетной структуры считали не равный нулю орбитальный момент атомного остатка.

Осенью 1924 г. я опубликовал ряд возражений против этой точки зрения, которую я окончательно отверг, как неправильную, и выдвинул вместо нее предположение о новом квантовотеоретическом свойстве электрона, которое я назвал "двузначностью. не поддающейся классическому описанию".

Здесь Паули имеет в виду следующую фразу из своей статьи "О влиянии зависимости электронной массы от скорости на эффект Зеемана", поступившей в редакцию в декабре 1924 г. и появившейся в начале 1925 г.: "... дублетная структура спектров щелочных металлов, а также отступление от теоремы Лармопа возникают вследствие характерной двузначности квантовых свойств электпона. которую нельзя описать классически".

В начале 1925 г. в Тюбинген где работали Ланде. Герлах и Бак, приехал из США молодой физик Р. Крониг. Ланде показал ему письмо от Паули, в котором говорилось, что в атоме, находящемся в сильном магнитном поле, каждый электрон должен характеризоваться четырьмя квантовыми числами: главным квантовым числом n. азимутальным квантовым числом l, магнитным квантовым числом m_l = m₂ + m_s и числом m₂ = m_l + 2m_s.", характеризующим энергию магнитного взаимодействия электрона с внешним полем. Далее Паули указывал, что в состоянии, характеризуемом четырьмя квантовыми числами, может находиться только один электрон. Обдумывая это письмо, Крониг пришел к выводу, что моделью, представляющей электрон с такой характеристикой, может быть вращающийся электрон. Он сообщил об этой идее приехавшему в Тюбинген Паули, который сказал, что "это очень остроумная выдумка", но не поддержал ее, считая, что установленная им "двузначность" не поддается модельному представлению. Следует отметить, что представление о вращающемся электроне было предложено с другой целью в 1921 г. А. Комптоном, но оно не оказало влияния на развитие теории эффекта Зеемана. Крониг пытался обсудить свою идею с Гейзенбергом, Крамерсом и Бором, но она не встретила поддержки. Выдвигались возражения, во-первых, связанные с множителем 2, во-вторых с неясностью вопроса, почему вращение электрона должно быть именно таким, чтобы получился магнетон Бора, в-третьих, с тем, что скорость вращения электрона должна превышать скорость света, что противоречило принципу относительности. Подавленный этими возражениями и холодным отношением к своей идее прославленных физиков Крониг отказался от публикации своих мыслей. Пуризм Паули в данном случае задержал развитие важной физической идеи, одной из центральных идей современной физики.

Авторы этой идеи Е. Гаудсмит и Г. Юленбек оказались счастливее Кронига. Они встретились у Эренфеста в Лейдене во время летних каникул. Гаудсмит уже хорошо освоил формализм описания сложных спектров и в начале мая 1925 г. опубликовал статью, в которой показал, что применение принципа Паули к теории мультиплетов можно значительно упростить, если применить магнитные числа Ланде m_l и m_s. Однажды он заговорил на эту тему во время совместной работы с Юленбеком и тот сразу понял, что это означает наличие у электрона четырех степеней свободы. Исследуя эту идею они пришли к представлению о вращательном моменте электрона (спине) и составили краткую заметку, которую Эренфест сразу же направил в "Naturwissenschaften". Когда Юленбек, выяснив, после тщательного изучения, что классическая модель вращающегося электрона, обладающего магнитным моментом, равным магнетону Бора, противоречит теории относительности, хотел было взять статью обратно, Эренфест ответил, что уже поздно и добавил: "Вы оба достаточно молоды, чтобы позволить себе делать глупости".

Статью Юленбека и Гаудсмита сразу заметил Гейзенберг и назвал ее "смелой". Ею заинтересовался также Бор. Однако Паули скептически отнесся к идее спина и только после изучения работы Томаса прислал Гаудсмиту открытку от 13 марта 1926 г., в которой взял свои возражения обратно.

В связи с этим Томас писал Гаудсмиту: "Я полагаю, что тебе и Юленбеку очень повезло, что ваша работа о вращающемся электроне была опубликована до того, как об этом услышал Паули.

Похоже, что Крониг более года назад думал о вращающемся электроне и что-то разработал по этому вопросу.

Первый человек, которому он это показал, был Паули.

Паули высмеял это дело до такой степени, что первый человек стал и последним, и никто больше об этом ничего не услышал."

В истории науки чрезмерная строгость может оказаться не только бесполезной, но и вредной при появлении новой идеи. Идея выкристаллизовывается и изменяется в течение некоторого времени и иногда бывает полезно отнестись не слишком придирчиво к сырой еще идее. Ей надо созреть в "рабочей обстановке".

Тем временем Паули опубликовал статью "О связи заполнения атомных оболочек в атоме со сложным строением поля", в которой он, опираясь на замечание английского физика Стонера, высказанное последним в статье, опубликованной в 1924 г., сформулировал свой знаменитый принцип. Стонер уточнил распределение электронов по группам и заметил, что при данном значении главного квантового числа число уровней оптического электрона щелочных металлов во внешнем поле равно числу электронов в замкнутой оболочке инертных газов, соответствующих значению этого главного квантового числа. "Тогда,- говорил Паули в нобелевской лекции,- на основе моих прежних результатов по классификации спектральных термов в сильном магнитном поле для меня прояснилась общая формулировка принципа запрета". В своей статье он формулирует этот принцип следующим образом: "В атоме не может существовать двух или больше эквивалентных электронов, для которых значения всех квантовых чисел n, k₁, k₂, m в магнитном поле одинаковы. Если в атоме находится электрон, для которого все эти числа имеют определенное значение, то это состояние "занято".

Квантовые числа Паули соответствуют современным значениям следующим образом: n = n,

Принцип Паули позволил ему определить число электронов на замкнутых оболочках и тем самым дать ключ к правильному пониманию периодической системы. В конце концов он пришел к идее "спина" как новой квантовой характеристики частицы, не поддающейся классическому описанию. Эта точка зрения стала общепринятой.