Ответы, решения, замечания (ОРЗ)

4. Сравнивая движение кометы и Земли, с помощью третьего закона Кеплера найдем большую полуось кометной орбиты: а= 18,05 а. е. Максимальное удаление от Солнца около 35,5 а. е.

5. Согласно расчету минимальное расстояние кометы Григга - Скьеллерупа от Солнца 0,77 а. е., т. е. комета подлетает к Солнцу ближе Земли. Это, однако, не дает возможности однозначно ответить на вопрос задачи. Как уже упоминалось, орбиты комет могут иметь заметный наклон к эклиптике. В этом случае пересечение проекций орбит планеты и кометы на плоскость эклиптики не гарантирует пересечения самих оргит. Так, мы знаем, что комета Галлея имеет перигелий на расстоянии 0,59 а. е. от Солнца, т. е. подходит к нему ближе орбиты Земли. С этой точки зрения вроде бы возможно ее столкновение с Землей. Когда перед 1910 годом астрономы радовались, что комета Галлея пролетит очень близко от Земли, поползли слухи о столкновении, о конце света. Но это "очень близко" - десятки миллионов километров. Минимальное расстояние между кометой и Землей зависит, естественно, не только от взаимного расположения их орбит, но и от того, где на своей орбите находится Земля, когда комета проходит мимо ее орбиты. В ближайшие несколько тысячелетий комета Галлея не окажется ближе 0,064 а. е. (около 10 млн км) от Земли. Наименьшее расстояние, на которое комета Галлея подходила к Земле, равно 0,04 а.е.=6 млн км. Это было в 837 году, когда орбита кометы была несколько иной.

6. Чтобы "превзойти" Евдокса, понадобится около 5 суток, Брате - почти месяц (25 суток), Улугбека - больше двух месяцев (почти 70 суток). И эти цифры еще следует считать заниженными, так как дифракционный предел, из которого мы исходили при расчете, - недостижимый идеал. Оптические приборы считаются отличными, если удается разрешить угол, вдвое превышающий дифракционный.

7. Аристарх вычислил, что Земля в 3 раза больше Луны. По современным данным - в 3,67 раза.

8. Из рис. 20 непосредственно видно, что отношение расстояний от Земли до Луны и от Земли до Солнца есть синус "угла Аристарха". Расчет по данным Аристарха дает отношение, равное 19, по современным данным получаем 400. Но даже по данным Аристарха диаметр Солнца в 6 с лишним раз больше диаметра Земли, а значит по объему Солнце больше в 250 раз. Трудно поверить, что такой гигант "крутится" вокруг крошечной Земли.

9. Эратосфен - 47,5 тыс. км, Посидоний - 45,6 тыс. км, современные данные - 40,0 тыс. км. Если же принять стадий равным 157 м, то Эратосфен получил 39,25 (!)Солнце а Посидоний - 37,68 тыс. км. И, такое ухудшение точности становится совсем непонятным, если вспомнить, что Эратосфен измерял высоту Солнца, которое само имеет угловой размер около 0,5°, а Посидоний - вы- Лииа соту звезды Канопус.

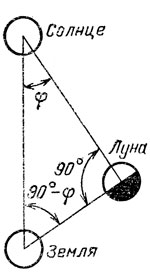
Рис. 20

10. Разность широт рассматриваемой точки и тропика определяет минимальный зенитный угол Солнца. Значит, в Самарканде Солнце не доходит до зенита 16°, в Булгаре - 32° - ровно вдвое больше. Можно, конечно, вычислить длины минимальных теней и сравнить их. Но на вопрос задачи можно ответить, не заглядывая в таблицу тангенсов. Достаточно вспомнить формулу tg2α=2tgα/(1-tg2α) и станет понятно, что tg2α больше 2tgα;. Значит, тридцатиметровая обсерватория отбрасывала меньшую тень, чем пятнадцати метровый минарет.

11. При движении к Юпитеру Земля получает сигнал об очередном затмении Ио раньше на время υ₃t₀/c, где с - скорость света, а t₀ - период обращения Ио вокруг Юпитера. При движении от Юпитера сигнал на такое же время запаздывает. Значит, действительное время между затмениями равно t₀=(t₁+t₂)/2, а кроме того, t₂-t₁=υ₃(t₂+t₁)/c. В результате получаем с=υ₃(t₂+t₁)/(t₂-t₁)=3,04×10⁵ км/с.

Погрешность ≈ 1 % естественна - примерно с такой точностью мы "замерили" разность времен между затмениями.

12. R_л= (g₀r₀²T²_Л/4π)^1/3=383 тыс* км (точное значение 384,4 тыс. км).

13. Примерно 275 м/с².

14. Приравнивая для Ио центростремительную силу и силу притяжения Юпитером, получаем M_ю=4π²R³/GT², где G=6,67×10^-11 Н*м²/кг² - гравитационная постоянная. Получаем М_ю=1,9×10²⁷ кг (около 318 масс Земли). Теперь ускорение силы тяжести на поверхности Юпитера можно вычислить двумя способами. Первый - путем сравнения масс и размеров Земли и Юпитера: g_ю/g₀=(М_ю/М₀)(r²₀/r²_ю). Второй - путем вычисления ускорения Ио: GM_ю/R²=4π²R/T², а затем, в соответствии с законом обратных квадратов, полученное значение умножим на квадрат отношения радиуса орбиты Ио и радиуса Юпитера, т. е. на 35,4. В любом случае получаем, что ускорение свободного падения на поверхности Юпитера g_ю=25,2 м/с².

15. υ_1к=√g₀r₀- Получаем для Земли 7,9 км/с, для Солнца - 437,5 км/с, Юпитера - 42,4 км/с.

16. Подобно тому, как это делалось в задаче 14, можно вычислить массу Солнца, а затем и его плотность: ρ_⊗= 1,4×10³ кг/м³.

Ясно, что минимальный период обращения вокруг Солнца имеет спутник, движущийся по "стелющейся" орбите. Это прямо следует из третьего закона Кеплера (окружность - вырожденный эллипс). Для этого периода получаем T^min_⊗=(3π/ρ_⊗G)^1/2=10⁴ с.

17. Посмотрим на рис. 21.

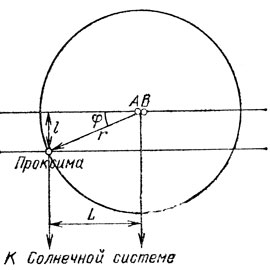
Рис. 21

Расстояние l=2,42×10³ а. е., а расстояние L=10,4×10³ а. е. (пересчет пусть читатель проверит сам). По теореме Пифагора найдем радиус орбиты Проксимы: Солнечной системе r=10,7×10³ а. е. Период обращения можно найти, сравнивая движение Проксимы с движением Земли: T_п= T₀ (r/R₀)^3/2(M_⊗/M_AB)^1/2=8×10⁶ лет. Нетрудно найти также угол φ=13°.

В задаче не оговорено, в какую сторону движется Проксима. Если она приближается к нам, то ближайшей она будет еще 370 тыс. лет, а если удаляется, то - "всего" 30 тыс. лет.

18. ρ_я=ρ_⊗(T^min_⊗/T_H)²= 1,4×10¹⁷ кг/м³. Нейтронная звезда в сто триллионов раз плотнее Солнца! Массы этих звезд всего в 2-3 раза больше массы Солнца, а значит, диаметр нейтронной звезды всего несколько десятков километров. Что там Земля! "Уважающий себя" астероид в десятки раз больше такой звезды!

19. 6,5×10¹⁰M_⊗. Напомним, что в этой задаче речь идет о звездах, которые ближе Солнца к центру Галактики. В следующей задаче фигурирует уже масса всей Галактики,

20. Период обращения Магеллановых Облаков (не будем утомлять читателя многократно использованными формулами) около 3 млрд лет. В телескоп ЕЮО можно зафиксировать угол 1,7×10^-7 рад. Такой угол Магеллановы Облака пройдут примерно за 80 лет.

22. Приняв за единицы измерения соответственно массу Солнца, радиус земной орбиты и земной год, для массы Сириуса В получим уравнение (2,3+x)²x³= 10,9. Подбором определяем x=1, т. е. масса Сириуса В примерно равна массе Солнца. Становится непонятным, почему такую звезду не видно невооруженным глазом. Ведь Солнце с Сириуса выглядит звездой второй величины - как Полярная. Оказывается, Сириус В - белый карлик. Это не нейтронная звезда, но все же звезда очень плотная, ее плотность в миллион раз больше плотности Солнца. Нетрудно подсчитать, что при равных массах поверхность такой звезды в 10 тысяч раз меньше поверхности Солнца (радиус карлика порядка радиуса Земли). Поэтому, хотя температура карлика в два с лишним раза выше температуры Солнца, он в сотни раз слабее Солнца как источник света.

23. Расстояние не изменилось, а масса возросла вдвое. Отсюда ответ - год уменьшится в √2 раз.

24. Звезды А и В движутся по окружностям радиусов |АО| =|ОВ| = r с некоторой угловой скоростью со. Второй закон Ньютона для них можно записать в виде GM/(2r)²=ω²r, Планета движется с той же угловой скоростью по окружности радиуса |ОС| = x под действием составляющих сил притяжения, направленных вдоль ОС. Запишем второй закон для нее: (2GM/R²)(х/R)=ω²x. Исключая очевидный случай x=0 и учитывая, что R²=r²+х², получаем x=r√3. Заметим, что |АС| = |ВС|==2r, т. е. треугольник ABC - равносторонний,

26. Относительно центра Земли это расстояние R=r₀√2, а высота подъема, следовательно, равна r₀(√2-1) = 2640 км.

27. υ_2к = √(2g₀r₀) = 11,18 км/с,

28. g_ю = g₀(М_ю/М₀)(r²₀/r²_ю);

υпар=υ_2к√(M_юr₀/M₀r_ю) = 60,1 км/с.

29. 42,1 км/с,

30. У поверхности Земли ракета должна обладать достаточной энергией, чтобы, выйдя из ее поля тяготения, еще иметь скорость 32,3 км/с. Вспомнив, что сложение энергий соответствует сложению квадратов скоростей, без труда получим 16,6 км/с. Направление скорости по выходе из поля тяготения Земли должно при этом совпадать с направлением орбитальной скорости Земли. Запуск надо очень аккуратно рассчитать. В частности, обратим внимание на такое обстоятельство. Предположим, мы попробуем запустить ракету со скоростью 16,6 км/с относительно центра Земли. Но эта скорость складывается из двух составляющих. Какую-то скорость сообщил ракете двигатель, и эта составляющая обычно направлена по радиусу Земли. А еще надо учесть скорость, связанную с суточным вращением Земли. А если говорить серьезно, то нельзя забывать и о сопротивлении воздуха...

31. Выразим в третьем законе Кеплера для круговых орбит период обращения через скорость и радиус: r₁³/r₂³=T²₁/T²₂=(2πr₁/υ₁)²/(2πr₂/υ₂)². Получаем υ₁/υ₂=√(r₂/r₁). Зная скорость Земли, легко вычислим круговую скорость для перигелия кометы Галлея: 29,8√(1/0,59) = 38,6 км/с. Параболическая скорость кометы больше в раз, т. е. равна 64,9 км/с.

32. 2υ.

33. υ_п = √(2GM_⊗/[r_п (1 + r_п/r_а)])- Прежде чем подставлять числовые значения, обратим внимание на то, что выражение √(2GM_⊗/r_п) - это параболическая скорость кометы в перигелии, которую мы вычислили в задаче 31. Теперь можно еще преобразовать то, что осталось. Учитывая малость величины r_п/r_а - обозначим ее x,- можно записать следующее: 1/√(1+x)≈(1+x/2)^-1≈1-x/2. Сразу видно, какого порядка погрешность мы допустили при оценке. Уточненный ответ - 54,4 км/с.

34. Это действительно очень просто: применим второй закон Кеплера к перигелию и афелию и немедленно получим, что в афелии комета движется "совсем медленно" - ее скорость равна 0,9 км/с. Приличный истребитель может соперничать с такой кометой.

35. Посмотрим на рис. 22. За время прохождения дальней половины орбиты радиус-вектор кометы заметает площадь фигуры СВАВ'. Площадь этой фигуры равна πаb/2+b(а-r_п). За время прохождения ближней к Солнцу половины орбиты - оставшуюся часть от площади πab. Расчет дает 14,7 года. Но в точках В и В' комета находится от Солнца на расстоянии равном большой полуоси ее орбиты. А это еще ой как далеко от Солнца - больше 18 а. е.! В наши дни (свидание 1986 года) с помощью сверхмощных ЭВМ удалось предсказать положение кометы с точностью до нескольких угловых секунд. Поиски велись на телескопе с 5-метровым зеркалом. И в телескоп "смотрел" не человек, а сверхчувствительный фотоприемник, способный регистрировать одиночные кванты света. И все же комету заметили лишь за три с небольшим года до прохождения перигелия, на расстоянии около 111 a. е. от Солнца. Таким образом, даже будучи вооруженными современной техникой, мы в состоянии следить за этой самой изученной кометой лишь в течение 1/12 периода ее обращения вокруг Солнца.

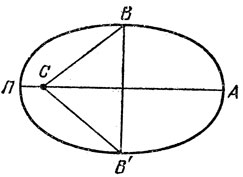
Рис. 12

36. Площадь, ограниченная всей орбитой Плутона, как мы помним, равна S=πab. Нам надо найти, какую площадь он заметает за время пребывания на месте восьмой планеты. Это площадь сектора эллипса. Вычислить точно ее нам не удастся. Но обратим внимание, что расстояние от Солнца в этот период меняется незначительно: в начале и в конце - 4,5 млрд км, а в середине - минимальное - 4,4 млрд км, т. е. по форме эта область похожа на сектор окружности. Если мы возьмем некоторый средний радиус, например (r+R₁)/2, то наверняка получим довольно точное значение площади S₁=(100π/360)×((r+R₁)/2)². Не знаю, убедит ли это читателя, но можно проверить, что если вместо квадрата среднего радиуса [(r+R₁)/2]², a мы возьмем средний квадрат радиуса (r²+R²₁)/2, то результат практически не изменится. В любом случае получаем для времени пребывания Плутона внутри орбиты Нептуна τ=TS₁/S=40 лет.

Значит, Плутон вновь станет девятой планетой в 2009 году, как и написано в астрономических справочниках.

33. Около 42 тыс. км.

39. Когда первый спутник находится в точке а, второй - в а' (рис. 23), когда первый - в b, второй - в b', Ясно, что участки а'а и b'b второй спутник должен пройти за одно и то же время,- это время, на которое он отстает от первого. Из второго закона Кеплера отношение Оа к Оb должно - быть равно 2 : 5. Большую ось орбиты найдем, например, сравнивая при помощи третьего закона Кеплера наш спутник со спутником минимального периода обращения. Получаем большую ось 25 570 км, и перигейный и апогейный радиусы соответственно 7306 и 18 265 км; не забудем вычесть радиус Земли и получим в ответе: 936 км в перигее, 11 895 км в апогее.

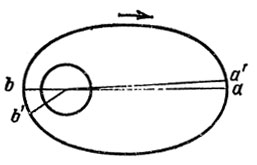
Рис. 23

40. Пусть в некоторой точке расстояние от центра притяжения r, а скорость υ, и направлена она перпендикулярно радиусу-вектору. Очевидно, это одна из крайних точек орбиты - допустим, перицентр^*.

^* (В общем случае ближайшая и наиболее удаленная от Центра притяжения точки называются соответственно перицентром и апоцентром. Если "светило" - Земля (Гея), то это перигей и апогей, для Солнца (Гелиоса) - перигелий и афелий. Придуманы названия для особых точек орбит спутников Луны (Селены) - периселений и апоселений; возле любой звезды (астры), кроме нашего Солнца,- периастр и апоастр.)

Попробуем найти расстояние до апоцентра R. Предположим, что скорость спутника в апоцентре равна V. Запишем второй закон Кеплера и закон сохранения энергии для этих двух точек (в расчете на единицу массы спутника):

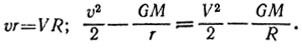
Исключим V:

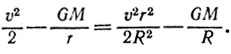
А теперь немного подумаем.

После приведения к общему знаменателю (R, по-видимому, не равно нулю) мы получим квадратное уравнение, имеющее два решения. Что это за решения? Это те значения R (r и υ мы считаем известными), для которых выполняются два наших уравнения. Это апоцентр и ... перицентр. Конечно, если неизвестный радиус равен г, а скорость - v, то наши уравнения обращаются в тождества.

Поразмыслим еще чуть-чуть. Нас интересует большая ось орбиты. Но это r+R, т. е. сумма решений преобразованного уравнения, Теперь ясно, что она будет равна отношению множителя при 1 /R в правой части уравнения к его левой части. Но в левой части - полная энергия единицы массы спутника. По-моему, все. Окончательно получим такую связь между большой полуосью орбиты а, полной энергией единицы массы обращающегося по этой орбите тела Е и массой центра тяготения М: 2a = -GM/E = GM/|E|.

41. Энергия крышки (мы все время говорим об энергии единицы массы) больше энергии спутника, значит ось ее орбиты больше. В месте старта скорость крышки перпендикулярна радиусу, значит, это перигей. Итак, орбита крышки будет выглядеть, как на рис. 24, только различие между орбитами на рисунке, конечно, преувеличено. Используя результаты задачи 40 и приближенную формулу, которую мы только что вспоминали, попробуем найти различие в больших осях орбит спутника и крышки:

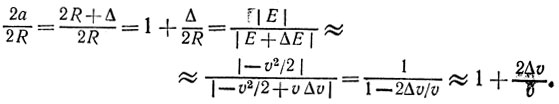
Читатель может проверить более подробна, но ответ получится тот же. Дальше получаем Δ=R×4Δυ/υ=32 км. Орбита ясна.

Рис. 24

42. Используя тот же прием, что и в задаче 41, применительно к третьему закону Кеплера, найдем разность периодов обращения спутника и крышки. Получаем ΔT=T(3Δ/4R)= 19 с. Давайте остановимся и обдумаем этот результат. Большая ось эллипса на 32 км больше радиуса круговой орбиты. Длина эллипса менее чем на πΔ= 100 км превышает длину окружности. Если пренебречь изменением средней скорости, то крышка должна опоздать всего на 12 с. Значит, средняя скорость крышки меньше скорости спутника, несмотря на то, что в перигее она даже больше. В общем, этого можно было ожидать. Ведь на круговой орбите, совершенно очевидно, чем больше радиус, тем меньше скорость. Так вот, средняя скорость на эллипсе, так мало отличающемся от окружности, близка к той, с которой тело движется по окружности радиуса, равного большой оси эллипса. Эти соображения нам пригодятся в дальнейшем.

43. В этом случае новая скорость крышки будет У изменение оси орбиты у Леонова вдвое меньше, чем у спутника, полуось новой орбиты отличается от радиуса всего на 8 км. Точка старта теперь не будет перигеем (рис. 25).

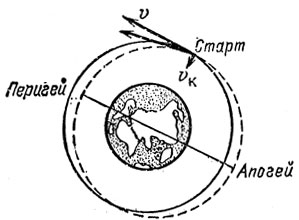
Рис. 25

44. К моменту встречи первый спутник должен пройти на l=53 км меньше полного оборота. Второй спутник к этому времени должен совершить полный оборот по новой орбите, а значит относительное изменение периода должно составить ΔT/T=l/2πR= 1,2×10^-8, Так как изменение орбиты мало, относительное изменение большой полуоси можно определить из соотношения Δа/R=2T/3T=8×10^-4. С точностью до знака таким же должно быть изменение полной энергии, а так как она может измениться только за счет изменения кинетической, то и изменение последней составит те же 8×10^-4. Изменить скорость надо, очевидно, на 4×10^-4. Осталось рассчитать скорость на исходной орбите, например, с помощью соотношения υ²R=υ²_1кr₀. В результате получаем

45. Вдали такой метеорит имеет скорость относительно Земли 59,6 км/с - это удвоенная скорость Земли. Кроме того, он наберет в поле тяжести Земли энергию, соответствующую второй космической скорости - 11,18 км/с. Из закона сохранения энергии ясно, что складываются квадраты скоростей. В результате получаем 60,64 км/с - как видим, если мы и забыли о приросте скорости, то ошиблись немного.

46. На удвоенном расстоянии от Земли скорость метеорита еще ближе к удвоенной скорости Земли (υ_м=60,1 км/с). Теперь сообразим, какой должна быть скорость спутника после столкновения, чтобы он попал на Землю. Большая ось орбиты, касающейся Земли (рис. 26), равна 3r₀, "старая" ось - 4r₀. Используя это соотношение (не забудем рассчитать сначала скорость на старой орбите - υ₁=5,59 км/с), зная, как связаны оси и энергии, найдем, что скорость должна упасть до υ₂=4,56 км/с. Закон сохранения импульса при ударе выглядит так: υ₁M-υ_Mm=υ₂(M+m). Отсюда m=16 кг.

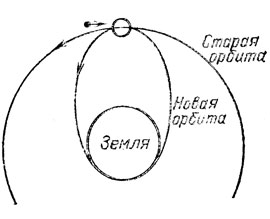
Рис. 26

48. Если увеличить скорость корабля υ на величину Δυ, то изменение кинетической энергии единицы массы

Отсюда ясно, что при большей скорости прирост энергии больше. Потенциальную энергию мы считаем неизменной, а полная энергия на орбите не меняется она одна и та же в апогее и перигее. Может быть, я слишком разжевываю решение, но очень хочется подчеркнуть неожиданный, на первый взгляд, результат: с близкого расстояния улететь легче, чем с далекого.

49. Первое, что приходит на ум, по крайней мере, автору,- вычислить потенциальную энергию на расстоянии 384 тыс. км от Земли, сравнить ее с энергией на поверхности Земли и недостачу восполнить за счет энергии кинетической.

Конкретный расчет можно произвести по-разному. Мне нравится такой способ. На поверхности энергия пропорциональна второй космической скорости, на орбите Луны она в 60 раз меньше, чем на Земле (60 - отношение радиуса орбиты Луны к радиусу Земли). Значит, энергия, необходимая для достижения орбиты Луны, составляет 59/60 "второй космической энергии", а скорость

Но тут возникает сомнение - стоит ли лететь до орбиты? И речь идет не о размерах Луны - читатель без труда убедится, что при нашей (разумной!) точности расчетов это ничего не меняет.

Но ведь если мы попадем в область, где притяжение Луны сильнее притяжения Земли, Луна сама затянет нас к себе в гости. А это немалое различие - Луна всего в 81 раз "легче" Земли, а это значит, что можно выиграть 1/10 расстояния. Но при этом вместо 1/120 выигрываем 1/108 скорости - понадобится не 11,09, а 11,08 км/с.

Далее, на Земле притяжением Луны можно пренебречь. Но в точке "пересадки" силы сравниваются. Почему же мы вообще забыли о притяжении Луны? Давайте учтем его. Тогд! потенциальная энергия в поле Луны к точке пересадки достигает величины (по модулю) (М_Л/М₀)(r₀/6r₀)= 1/486 "второй космической энергии"! Опять мелочи.

Оказывается, первая оценка очень хороша? Поживем - увидим.

50. Казалось бы, надо достичь скорости чуть меньшей, чем вторая космическая, а значит, это практически повторение задачи 47. Но в этом варианте у корабля есть горизонтальная составляющая скорости, значит, в силу второго закона Кеплера (момент импульса должен сохраняться) в точке пересадки полная скорость не может обратиться в нуль. Однако она упадет в 54 раза, а значит составит (опять мелочи!) примерно 0,2 км/с.

51. Можно попробовать такой способ. Рассчитаем для нашего расстояния от Луны R=38,4 тыс. км круговую скорость, а потом сообразим, во сколько раз отличается ось нашей орбиты от R, Итак, круговая скорость пропорциональна M/R и ее можно вычислить из первой космической:

Но постойте, это втрое меньше нашей скорости. А параболическая лишь в √2 раз больше круговой. Значит, мы опять не попадем на Луну! Только-только пересев в ее сферу притяжения, мы тут же начнем от нее уходить на бесконечность! Надо срочно тормозить.

52. Поскольку мы находимся на расстоянии, в 48 с лишним раз превышающем радиус Луны, а нас устраивает только орбита, касающаяся поверхности Луны, большая ось должна быть чуть больше R. Примем ее в качестве первого приближения равной R. Круговая скорость определяет кинетическую энергию на круговой орбите. Кинетическая энергия единичной массы будет υ_кр²/2, а потенциальная равна -υ²_кр. Тогда полная энергия будет -υ²_kp/2.

Нам необходима полная энергия вдвое большая, причем изменять мы можем только кинетическую энергию. Запишем соотношение в общем случае, для произвольного изменения полной энергии, например для увеличения в n раз большой оси по сравнению с круговой орбитой: (υ²_kp/2-²_kp)n=υ²_n/2-υ²_kp. Тогда для нашего приближения (n = 1/2) немедленно получаем υ²_n=υ²_kp(2-1/n)=0!

Так ли уж это неожиданно? Чем меньше скорость, тем ближе перицентр будет смещаться к центру притяжения. В пределе - при нулевой скорости - эти точки совпадут, т. е. орбита вырождается в отрезок прямой, соединяющей точку, где тело "замерло" в неподвижности, и центр притяжения. Этот результат нам еще пригодится.

А чтобы, наконец, сесть на Луну, надо снизить скорость до 0,07 км/с.

53. В первом приближении орбита Марса в N=1,5 раза больше орбиты Земли. После выхода из поля тяготения Земли ракета по условию неподвижна относительно Земли. Относительно Солнца, в чьем поле ракета теперь должна лететь, она имеет круговую скорость 29,8 км/с. Теперь надо перейти на орбиту с n=(N+1)/2. Дополнительная скорость - 2,84 км/с.

Однако вспомним, что орбита Марса заметно отличается от окружности. Минимальное расстояние до Марса - в великом противостоянии - всего 56 млн км. И если мы прицелимся в перигелий Марса, то понадобится только 2,26 км/с дополнительной скорости.

54. В момент изменения направления скорости энергия ракеты не меняется. Значит, не должна измениться большая ось орбиты, т. е. радиус такой круговой орбиты равен большой полуоси начальной орбиты, в нашем случае - около 43 тыс. км.

Подчеркнем, что изменение скорости будет значительным. Скорость - вектор. Посмотрим на рис. 27. Очевидно, что менять скорость придется в конце малой оси. Для достаточно вытянутой траектории - эллипса с большим эксцентриситетом - скорость надо повернуть почти на 90°. Если ракета падает из неподвижного состояния, то угол, конечно, в точности прямой. Изменение скорости тогда в √2 раз больше самой скорости в этой точке.

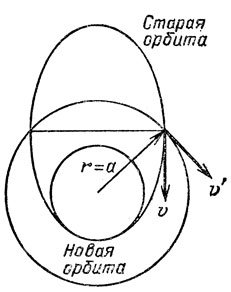
Рис. 27

55. Круговая скорость у поверхности Луны υ₀=1,68 км/с. На удвоенном расстоянии от поверхности круговая скорость в √2 раз меньше: υ₁=1,19 км/с, а параболическая (в √2 раз больше круговой) как раз равна υ₀. Значит, нам надо набрать Скорость V=0,49 км/с.

Пересядем в систему "корабль". Перед началом маневра В этой системе корабль по определению неподвижен. После срабатывания двигателя масса корабля изменяется на величину m=М₀-М. Газы массы m вылетают со скоростью u=4 км/с (как мы договорились раньше), а "остаток" должен иметь скорость V. Значит, um=V(М-m), откуда m=МV/(u+V). В нашем случае масса израсходованного топлива составит 10,9 % массы корабля.

56. Мы уже неоднократно переходили с орбиты на орбиту. Поэтому приведем только числовые результаты для проверки. Необходимая скорость - 1,61 км/с, изменение скорости - 0,42 км/с, расход топлива - 9,5%.

Заметим, что минимальная скорость, при которой можно достигнуть места пересадки, определяется законом сохранения энергии и равна 1,60 км/с. Но в этом случае она должна быть направлена по радиусу точно от центра Луны, чтобы момент импульса был равен нулю. Тогда на максимальном удалении от Луны скорость может обратиться в нуль. Но вектор изменения скорости при этом получается вычитанием двух взаимно перпендикулярных скоростей (рис. 28), а его модуль равен 2 км/с.

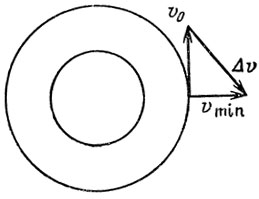
Рис. 28

Расход топлива оказывается больше того, который необходим для ухода на бесконечность.

57. Теперь можно все сравнивать с приземной орбитой. Расстояние (от Земли) равно 54,3 r₀, скорость - u=0,87 км/с. Находим, что большая ось орбиты будет равна 80,8 r₀, а нам нужно иметь 55,3 r₀. Расчет дает, что при переходе с орбиты на орбиту сразу в точке пересадки надо израсходовать массу топлива, равную 14,3 % имеющейся массы корабля, т. е. 12,9 % той массы, что корабль имел на окололунной орбите. Всего, значит, топливо должно было составлять 22,4 % массы корабля.

Остается одно сомнение: почему мы поспешили перейти на посадочную орбиту? Может быть, стоило это сделать, например, в перигее орбиты, на которую мы попали? Ведь в перигее легче изменить энергию. Но нам понадобятся разные изменения энергии!

В общем случае сравнивать переход на посадочную орбиту в перигее и апогее утомительно. Рассмотрим предельный случай. Пусть корабль движется по очень вытянутой орбите. Тогда в перигее его скорость мало отличается от параболической для этого расстояния. Нам надо попасть на орбиту, ось которой меньше расстояния до Земли, т. е. скорость должна стать меньше круговой для этого же расстояния. Значит, изменение скорости должно составить, как минимум, примерно √2-1≈0,4 круговой (опять же, конечно, для перигейного расстояния). А на большом расстоянии сама скорость гораздо меньше перигейной, уменьшать же ее до нуля не придется. Ясно, что при этом топлива потребуется совсем немного. При любых конкретных параметрах орбиты расчет подтвердит этот вывод.

58. Скорость кометы Галлея вблизи орбиты Земли примерно равна параболической, т. е. 42,1 км/с. Можно ее вычислить точнее (вспомним задачи 31 и 33), но вряд ли это стоит делать, так как мы довольно приблизительно описываем встречу "Веги" с кометой.

Как эта скорость направлена? Тут нам поможет второй закон Кеплера. Посмотрим на рис. 29. Если в перигелии заметаемая радиусом-вектором площадь определяется всей скоростью кометы υ_п, то в точке встречи-только составляющей υ_⊥. Скорость в перигелии мы знаем - это округленно 55 км/с. В точке встречи υ_k=42 км/с. Второй закон Кеплера дает возможность вычислить cosφ=r_пυ_п/R₀υ_к=0,77. По теореме косинусов (не забудем, что угол π - φ между υ_к и υ_в тупой) получаем относительную скорость "Веги" и кометы - 68 км/с. В действительности она была еще больше - около 78 км/с.

59. Конечная масса должна составлять одну двадцатиче-тырехмиллионную долю начальной! Следовательно, чтобы развернуть в погоню за кометой 1 грамм "Веги" (корпус аппарата, защита, приборы и т. п.), необходимо израсходовать 24 тонны топлива!

60. Оторвавшись от Земли, корабль должен иметь небольшую скорость относительно Солнца. Мы почти не ошибемся, если примем, что скорость относительно Земли равна 29,8 км/с. Тогда получим, что υ_4к=31,8 км/с. Согласно формуле Циолковского на полезную нагрузку (плюс корпус, баки и т. д.) придется меньше 0,04 % стартовой массы. В ракете, уже вылетевшей из сферы притяжения Земли с нулевой скоростью (и со скоростью 29,8 км/с относительно Солнца), на полезную нагрузку придется побольше - почти 0,06 %. Не густо...

61. Мы движемся по круговой орбите с длиной оси 2R₀, а хотим попасть на орбиту с длиной оси 6,2R₀, поскольку от Солнца до Юпитера 5,2 а. е. Такие расчеты мы уже проводили. Нужна прибавка скорости 8,8 км/с. Следовательно, 88,9 % стартовой массы должно составлять горючее.

62. Ответ однозначен - 5,65 км/с. Действительно, все планеты обращаются вокруг Солнца в одном направлении, поэтому геометрия нашего полета такая, как на рис. 30. Скорость Юпитера - 13,07 км/с - найдем с помощью третьего закона Кеплера, скорость корабля - 7,42 км/с - дает второй закон Кеплера.

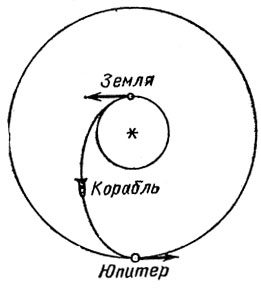
Рис. 30

63. Максимум скорости мы можем получить при сонаправленных скоростях корабля и Юпитера - это 18,67 км/с. А параболическая скорость корабля в √2 раз больше скорости Юпитера - 18,48 км/с! Топлива не надо.

64. Скорость кометы вблизи Юпитера (параболическая) равна 18,48 км/с. Она перпендикулярна скорости Юпитера, значит их относительная скорость составит 22,64 км/с. С этой же скоростью относительно Юпитера комета уйдет из его сферы притяжения. Но если комета развернется так, что скорости вычтутся, то относительно Солнца ее скорость станет всего 9,57 км/с. Это и есть" скорость в афелии. Привычный уже нам расчет дает расстояние в перигелии 2,18 а. е.

65. Из третьего закона Кеплера получаем большую полуось орбиты; она равна 8,78×10⁴ а. е. Затем методом, описанным в решении задачи 35, находим минимальное и максимальное расстояние до Солнца - соответственно 1,56×10⁴ и 1,60×10⁶ а. е.

66. Первыми сдвинутся с места кометы в точке В (рис. 31). Расстояние ОВ по главному свойству эллипса равно большой полуоси орбиты Немезиды. Для кометы, падающей на Солнце без заметной начальной скорости из точки В,- это большая ось орбиты. Нетрудно подсчитать, что кометы из точки В попадут на Солнце через 4,6 млн лет (полпериода) после начала движения, т. е. после прохождения Немезидой точки В (назовем этот момент началом эры Немезиды - э. Н.). Кометы из точки Вестественно, запоздают на время пребывания Немезиды в банке, т. е. они придут в 10,8 млн году э. Н.

Но в 3,1 млн году э. Н. Немезида будет в перигелии - всего в 1,56×10⁴ а. е. от Солнца, откуда кометам всего 0,35 млн лет лёту до Солнца. И эти кометы "откроют душ" в 3,45 млн году э. Н., т. е. на 1,15 млн лет раньше, чем кометы, прилетевшие из точки В. В таком случае кометный "душ" продолжался бы 7,35 млн лет.

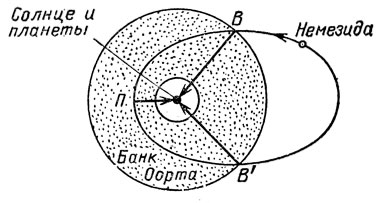
Рис. 31

67. Пересядем в систему отсчета, связанную с Солнцем (рис. 32). К Солнцу из бесконечности летят частицы со скоростью υ_пек=20 км/с. Какие из них врежутся в Солнце, какие пролетят мимо? Запишем для перигелия выражения энергии и момента импульса и приравняем их соответственно значениям при бесконечном удалении от Солнца. Плечо импульса - расстояние а - обычно называется прицельным параметром. Вычислим значение прицельного параметра, при котором перигелий от стоит от Солнца на расстояние r_⊗. Все частицы внутри цилиндра радиуса а₀ попадут на Солнце. Получаем

Мы не подумали, что частицы могут притормозить Солнце, но ответ нас успокаивает на этот счет.

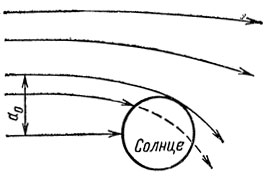
Рис. 32

68. Частица, находящаяся на расстоянии r от центра, начинает падение на центр в поле тяготения "внутренней" массы m_r=⁴/₃πr³ρ. Предположим, что она все время падает, не обгоняя внутренние частицы и не отставая от внешних. Тогда время ее падения - полупериод кеплеровой орбиты с осью r в поле тела массы m_r - равен

Как видим, r выпало из ответа, все частицы придут одновременно, так что наша модель, по-видимому, правильна. Так как плотность звезды гораздо больше плотности глобулы, а радиус соответственно меньше, разумным кажется и выбор полупериода в качестве времени падения.

Конечно, со временем частицы начнут сталкиваться, нагреваться, возникнут другие силы, помимо гравитационных. И все же оценка остается разумной, так как увеличение плотности всего на один порядок величины занимает более 80 % всего времени. Кстати, читатель может сам оценить эту величину, применив решение задачи 35 или 65 к эллипсу, выродившемуся в отрезок прямой (фокусы такого эллипса - на концах отрезка).

69. Звезды обращаются вокруг общего центра масс (рис. 33). Ясно, что скорость напарницы V/10=40 км/с. Полная кинетическая энергия системы 11M_⊗V²/20. Потенциальная энергия, равная -GM_⊗10M_⊗/R, как мы помним, по модулю должна быть в 2 раза больше кинетической. Из этих соображений получаем R=7,5×10⁹ м = 7,5 млн км.

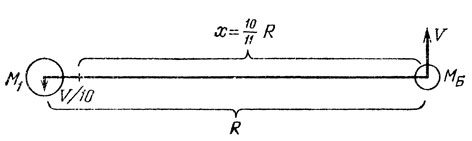
Рис. 33

70. Пересядем в систему центра масс. Звезда Барнарда движется со скоростью 400 км/с, остаток - со скоростью 40 км/с в противоположную сторону. Скорость центра масс υ_{ц. м} = 180 км/с, скорости звезд в системе центра масс V_ц - по 220 км/с. Из закона сохранения энергии 2M_⊗V²_ц/2-GM²_⊗/R=2M_⊗V²_∞/2 найдем, что при бесконечном удалении скорости звезд (относительно центра масс) V_∞= 175 км/с. Абсолютные скорости звезд равны соответственно 355 и 5 км/с.

71. Пусть k - отношение массы остатка к массе Солнца (и спокойной звезды). Тогда скорость центра масс

а скорости спокойной звезды и остатка равны соответственно V×11k/(10(1+k)) и V×11/(10(1+k)). Для того чтобы пара распалась, полная энергия должна быть равна нулю (или больше нулю): (M_⊗V²/2)×((121k(k+1))/(100(1+k)²)=GkM_⊗/R. Решая это уравнение, получаем k = 4,5 или k = 1. В первом случае пекулярные скорости звезд (они, конечно, равны скорости центра масс) получаются по 40 км/с. Эффект пращи не сработал. Обратим внимание на то, что невыразительная цифра 4,5 скрывает замечательное по своей простоте соотношение: система распадается при потере половины суммарной массы. Действительно, до взрыва масса системы составляла 11M_⊗, а после взрыва остается 5,5M_⊗.

Второй случай лишен физического смысла. Может показаться, что ему соответствует некая модель, хотя и весьма экзотическая. Предположим, что в результате взрыва из массы 10M_⊗ получилось 11M_⊗ вещества и M_⊗ антивещества. Конечно, никакого запаса энергии не хватит, но фантазировать так фантазировать. Но нет, и эта модель не проходит. Насчет гравитационного взаимодействия вещества с антивеществом ученые еще спорят; если право большинство, то вещество и антивещество должны притягиваться друг к другу, а мы при отрицатель-" ном значении одной из масс получим положительную потенциальную энергию, что соответствует отталкиванию. И уж наверняка кинетическая энергия "антизвезды" должна быть положи-" тельной величиной. Хотя речь идет об "антизвезде", все равно, чтобы ее разогнать, надо поработать.

Вообще, взрывы звезд - не такая уж редкость. Но такие, какие рассчитывали мы в предыдущей задаче,- от звезды массы IOMQ остается всего лишь Mq или чуть больше, происходят а нашей Галактике один-два раза в тысячелетие. Один из такнл взрывов сверхновой наблюдал и подробно описал Тихо Браге в 1572 году. Открытие сыграло дважды положительную роль в астрономии. Во-первых, как доказал Браге, Новая вспыхнула на сфере неподвижных звезд. Значит и там, вопреки Аритотелю, может что-то меняться.

Во-вторых, публикация Браге своих наблюдений резко подняла его авторитет, что немало способствовало получению кредитов у императора на постройку знаменитого Ураниборга.

Надо сказать, что китайцы и здесь опередили европейцев. Их астрономы подробно описали вспышку Сверхновой 1054 года - на этом месте сейчас видна знаменитая Крабовидная туманность. Кстати, как же все-таки правильно - новые или сверхновые? Астрономы употребляют приставку "сверх", не имея в виду, что эти звезды новее. В данном случае смысл приставки - еще большее изменение блеска, чем у "обычных" новых. С интересующей нас точки зрения отличия таковы: при взрыве новой улетает 0,001 % ее массы со скоростью порядка 100 км/с; у сверхновой - значительная часть массы (десятая, половина, девять десятых - как повезет) разлетается со скоростью больше 1000 км/с. Так что звезда Барнарда, если мы угадали причину ее высокой скорости, разогналась при взрыве сверхновой.

72. На парус действует сила светового давления F₀ = 10⁵ Па×5×10⁶ м²=50 Н. "Диана" движется в поле тяготения Солнца по орбите Земли. Следовательно, на нее, как и на Землю, действует сила притяжения f₀=υ²₀/R₀=6×10^-3 м/с? в расчете на единицу массы (6×10^-3 Н/кг). Если масса корабля равна m₀ = F₀/f₀ = 8,33 т, силы уравновешиваются и яхта будет двигаться по прямой. Более 6 т может хватить на корабль и снасти. Как же все-таки узнать максимально допустимую массу?

Очень важно заметить, что обе силы - гравитационная и сила светового давления - убывают с изменением расстояния от Солнца по одному закону: f= f₀R²₀/R², F=F₀R²₀/R². Ситуация такова, как будто происходит движение в поле тяготения тела, масса которого меньше массы Солнца. Можно ввести эффективную массу Солнца М_эфф=M_⊗-F₀R²₀/Gm и рассчитывать движение яхты в "исправленном" поле тяготения.

В общем случае так и надо поступать. Нашу конкретную задачу мы попробуем решить несколько иначе. Во-первых, тело, движущееся по орбите Земли в поле "нормального" Солнца, имеет кинетическую энергию mυ²/2=mf₀R₀/2. Потенциальная энергия такого тела, как мы знаем, U=-mf₀R₀. Полю сил светового давления может быть поставлена в соответствие потенциальная энергия U'=+F₀R²₀/R - это нетрудно понять, сравнивая выражения для гравитационной силы и силы светового давления. Для ухода на бесконечность нужна нулевая полная энергия. Получаем m₁=2m₀= 16,66 т. Вполне приличная масса - больше 14,5 т, если не считать парусов.

73. Понятно, почему задано такое нелепое значение для массы,- это просто 2m₁=4m₀. Теперь нетрудно составить баланс энергий. Надо сравнить энергию "Дианы" с энергией тела той же массы в поле одних сил тяготения и, используя связь полных энергий с осями орбит, определить афелий яхты, который равен 3R₀ (3 а. е.).

74. Пусть одна порция горючего сообщает кораблю скорость V. После сжигания двух порций у корабля (на единицу массы) будет кинетическая энергия 2υ². Так как он при этом оказывается на круговой орбите, его потенциальная энергия будет -4υ², а полная - (-2υ²). При сжигании одной порции горючего он получает кинетическую энергию υ²/2, а потенциальная энергия остается прежней. Итого получается -7υ²/2, Нетрудно подсчитать, что корабль находился на расстоянии 7 радиусов звезды от ее центра (точка касания - периастр орбиты, так как по условию одной порции хватило в обрез).

75. Очевидно, надо найти точку орбиты, в которой после сжигания второй порции горючего полная энергия корабля становится равной нулю. Может быть, эту задачу судорожно решал командор? Вряд ли, на это, оставалось время после первого маневра. Пусть второй пуск двигателя можно осуществить на расстоянии xR от центра звезды. Если на расстоянии 7R потенциальная энергия равна -4υ², то в точке х она равна -56 υ²/х. Та-кой же по модулю, но положительной должна быть кинетическая энергия. К точке старта корабль подлетает с полной энергией - 7υ²/2; выражение для потенциальной энергии в этой точке мы уже записали. Можно найти выражение для скорости, с которой корабль подлетает к старту. А еще он может увеличить ее на и. Получим уравнение

Отсюда x=3,5. Таким образом, вторую порцию можно было пускать в ход уже на расстоянии, большем 3,5 радиуса звезды ^от ее центра, т. е. 2,5 радиуса от поверхности.

76. Расчет приводит к трансцендентному уравнению, а в этот раз времени у командора было в обрез, как и горючего.

Допустим, на первом этапе израсходована доля топлива k, т. е. скорость корабля была kυ; υ как мы помним,- скорость на круговой орбите радиуса n (радиус звезды примем за единицу). Полная энергия получается k²υ²/2-υ², а для круговой орбиты с длиной оси, равной 2n, энергия будет -υ²/2. Большая ось орбиты, следовательно, равна 2n/ (2-k²). По условию эта величина есть n+1. С другой стороны, скорость в периастре, равная, очевидно, kυn, должна на (1-k)υ отличаться от параболической скорости υ√2n. Исключая одну из неизвестных величин, приходим к трансцендентному уравнению относительно другой, например: 2 + k - 2k² = √(2(2 - k²)).

Здесь, конечно, нетрудно освободиться от иррациональности. Но тогда мы придем к полному кубическому уравнению.

Получается, что корабль был на расстоянии 3,3 радиуса звезды от ее центра; расходуя 0,682 имеющегося топлива, он как раз попадал на орбиту с периастром на поверхности звезды. А там оставшихся 31,8 % топлива достаточно для перехода на параболическую орбиту. Вот это и считал командор.

77. Перед сближением потенциальная энергия отсеков U=-GMm (1/(R+l)+1/(R-l)). После сближения, если оба отсека оказываются на расстоянии R от центра Земли, получается U₁=-2GMm/R. Разность энергий

Пренебрегая отличием знаменателя от единицы, для относительного изменения потенциальной энергии получаем

Оценим эквивалентное изменение расстояния от Земли: |ΔU/U|≈|ΔR/R|. Следовательно, ΔR≈l×l/R действительно гораздо меньше l.

К сожалению, прирост полной энергии оказывается еще гораздо меньшим. Дело в том, что, раз возрос радиус, в силу закона сохранения момента количества движения должна уменьшиться скорость, т. е. кинетическая энергия. Прирост потенциальной энергии и уменьшение кинетической почти равны. Несколько более подробный анализ показывает, что полная энергия все же возрастает. Качественно это понятно: работа против силы тяжести (она совершается над ближним отсеком) больше работы силы тяжести (над дальним отсеком),- сила больше.

Однако количественно эффект очень мал - относительное изменение полной энергии порядка (l/R)⁴. Все же энергия растет, а значит, если времени достаточно, можно, сдвигая и раздвигая в подходящие моменты времени отсеки, потихоньку уползти от планеты. Ясно, что раздвигать отсеки желательно тогда, когда спутник ориентирован вдоль орбиты: тогда работа против силы тяжести равна нулю.

При таком маневрировании, вернее, при расчете его эффективности, возникает масса осложнений. Мы вынуждены учитывать различие в силах, действующих на отсеки,- на этом основан гравилетный способ полета. Но это означает, что возникает момент сил тяжести, спутник приходит во вращение... Поэтому не будем углубляться.

78. Чтобы "законопатить" дырку в Земле, надо добавить шар плотности ρ-ρ₀=ρ_эфф. Значит, силу притяжения при наличии полости можно рассматривать как сумму силы притяжения сплошной Земли и силы отталкивания - в действительности нехватку силы притяжения. Можно то же самое сказать другими словами: добавим шар радиуса r с плотностью, равной разности плотностей породы и воды, но припишем этой плотности отрицательное значение. Тогда потенциал в нижней точке впадины запишется следующим образом: - GM/(r₀-h)+G⁴/₃πr³ρ_эфф/(r+H). Полость гораздо меньше Земли в целом, ее влияние вдалеке ничтожно мало. Запишем потенциал там, где влиянием полости можно пренебречь: - GM/r₀. Обе точки находятся на поверхности океана. Приравнивая их потенциалы, получаем ⁴/₃πr³ρ_эфф/(r+Н)=Мh/r₀(r₀-h)≈Mh/r²₀, Если пред-положить, что радиус полости настолько велик, что в знаменателе левой части Н можно пренебречь, получаем 21 км. Более точное значение - 23,6 км.

79. Весь момент количества движения переходит к Луне. Величина m_Лυ_ЛR_Л должна возрасти на 20 %. Но закон Кеплера требует постоянства υ²_лR_л. Получаем новое расстояние до Луны R_л'=R_л×1,2²=553 тыс. км. Новый месяц Т^Л = Т^Л₀1,2³=47,2 сут.

80. Сила, действующая на спутник, мала. А что, собственно говоря, это значит? По сравнению с чем мала? Ну, видимо, по сравнению с силой притяжения к Земле - это, так сказать, главная сила. Например, в качестве первого приближения вычислим, какую работу совершит сила трения, если считать орбиту неизменной. Полньютона на 40 с небольшим тысяч километров - около 20 МДж. А кинетическая энергия корабля массы 10 т при скорости почти 8 км/с - около 300 тыс. МДж. Но кинетическая энергия не может уменьшиться, даже на тысячные доли процента, без изменения орбиты. А какая орбита подходит для нового значения энергии?

Предположим, что орбита осталась круговой, а полная энергия по модулю равна кинетической. Значит, если изменение энергии (потери на трение) составляет за оборот 0,0066 % начальной кинетической, то такую же долю оно составляет от полной энергии. Итак, полная энергия уменьшилась, а модуль ее возрос на 0,0066 %. За сутки такой спутник совершит чуть больше 16 оборотов. Энергия, а значит и полуось орбиты, изменится примерно на десятую долю процента. Спутник потеряет около 7 километров высоты. А скорость, кинетическая энергия? Они, конечно, увеличатся - на более низкой орбите скорость больше! Этот разгон с помощью тормозящей силы и называют парадоксом спутников.

С энергетической точки зрения тут все вроде бы ясно. Но интересно все же проследить, как сила, направленная против скорости (1), увеличивает скорость.

Предположим, летит себе спокойно спутник без сопротивления, а в какой-то момент "включают" тормозящую силу. Тогда спутник, потеряв немного кинетической энергии, перейдет на эллиптическую орбиту с апогеем в точке включения силы. Скорость перестает быть перпендикулярной силе тяжести (рис.34), возникает составляющая силы тяжести, ускоряющая спутник. И эта составляющая оказывается больше тормозящей силы. Скорость растет.

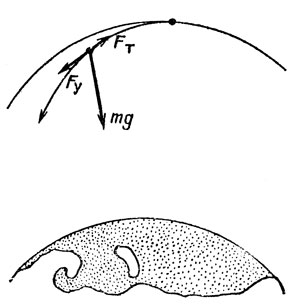
Рис. 34

81. Рассмотрим для примера ближайшую к Юпитеру глыбу (рис. 35). Распад роя означает, что расстояние между этой глыбой и центром роя возрастает.

Рой как целое падает на Юпитер с ускорением, которое ему сообщает сила притяжения Юпитера: a₁=GM_ю/R². В то же время рой сообщает глыбе ускорение a₂=Gm_p/r² а Юпитер - a₃=GM_ю(R-r)².

Если а₃ - a₂ > a₁ рой начинает распадаться. Полагая R>>r, получим 2rМ_ю/R³>>m_р/r²; R<<r׳√(2М_ю/М_р)=1,26 млн км. Читатель без особого труда докажет (легко показать), что то же самое условие получится для любой глыбы на прямой центр Юпитера - центр роя.

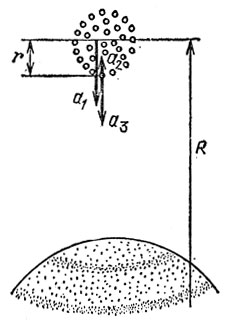
Рис. 35

82. Надо вычислить радиус звезды, у которой при плотности Солнца скорость убегания равна скорости света. Получаем 485 радиусов Солнца, у Мичелла - 500. Не менее интересен вопрос, при каком радиусе звезда с массой Солнца стала бы черной дырой; оказывается, 3 км. Эту величину - в соответствии с ОТО-вычислил Шварцшильд и получил r_ш=2GМ/с²- в точности по Мичеллу. Опубликовал этот результат Лаплас, первым получил Мичелл, а радиус Шварцшильда

83. Заранее положим, что частота изменится мало. Во-первых, радиус Солнца гораздо больше, чем расчетный радиус Шварцшильда, а во-вторых, в правомерности этого предположения нас уверит ответ. Запишем, что изменение энергии "тела" массы hυ/c² - при удалении с поверхности Солнца на бес-конечность равно hΔυ. С точки зрения СТО закон всемирного тяготения не изменился. Получаем относительное изменение частоты Δυ/υ=GM_⊗/r_⊗c²=g_⊗r_⊗/c²=2,13×10^-6. Обратим внимание, что в ответе получилась безразмерная величина.

84. Работа по удалению массы hυ/c² на небольшое расстояние ΔR совершается за счет убыли энергии кванта -hΔυ. Приходим к соотношению, сходному с тем, которое привело нас к формуле Циолковского: Δυ/υ=-(GM/R²c²)ΔR. Читателю, не знакомому с интегрированием, придется поверить на слово, что для звезды радиуса г отношение начальной и конечной частот, как в формуле Циолковского, зависит по экспоненциальному закону от знакомой нам безразмерной комбинации: υ₀/_v=e^GM/rc2. в нуль частота обратится только при нулевом радиусе.

85. Луч отклоняется ничтожно мало. Пренебрежем тем, что скорость света не меняется, и посчитаем, какой импульс получит фотон в поперечном направлении, как будто продольный импульс не изменился (рис. 36). Но сначала обратим внимание на то обстоятельство, что угол - величина безразмерная. С такой величиной, по-видимому, имеющей отношение к нашей задаче, мы только что встречались - это GM/rc². Для Солнца GM_⊗/r_⊗c²=2,13×10^-6. Трудно поверить, что эта цифра не имеет отношения к ответу.

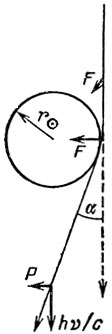
Рис. 36

Максимальное значение силы -(hυ/c²)(GM_⊗/r²_⊗). Но уже при удалении от ближайшей к центру Солнца точки на расстояние r_⊗ сила убывает в 2 раза, а поперечная составляющая - почти в 3 раза. Много ли наберется на еще больших расстояниях? Так что примерно на пути 2r_⊗ действует сила, мало отличающаяся от максимальной, а потом - быстро убывающая. Время действия максимальной силы - 2r_⊗/c. Значит, нашу оценку разумно удвоить.

ОТО дает 4GM_⊗/r_⊗c²≈8,5×10^-6 радиана (1,75").

86. Мы знаем два факта: то, что отклонение луча света Солнцем составляет 1,75", и то, что это отклонение пропорционально отношению М/R. Не забудем, что искомый угол А - Земля - В вдвое меньше угла отклонения луча А - Галактика - В. В результате получаем 5,8".

87. Опустим перпендикуляр ГД из Г на АЗ (рис. 37; обозначения на рисунке достаточно очевидны: 3 - Земля, Г - галактика, создающая эффект гравитационной линзы, А - квазар). Запаздывает определяется разницей путей: (АГ + ГЗ) - (АД + ДЗ) = cτ, где с - скорость света. Нетрудно найти ГЗ - ДЗ = Δl=l - lcosα =l(1 - √(1-sin2α)≈ l(1-√(1-α²)) ≈ 4,5×10^-3 св. лет = 1,42×10⁵ св. с. Теперь можно вычислить АГ - АД = Δx = cτ - Δl = 3,1×10⁴ св. с. С другой стороны, можно по аналогии с Δl написать Δx=xβ²/2. Наконец (учтем малость углов), ГД=h=lα=xβ. Комбинируя это соотношение с выражениями для Δl и Δx, получим lΔl=xΔx=h²/2. Следовательно, х=lΔl/Δx=4,58×10⁹ св. лет. Расстояние АЗ = АД + ДЗ ≈ АГ + Г3 = 5,58×10⁹ св. лет.