Пузырьковая модель кристалла (Я. Гегузин)

Слово о моделировании

На трудном пути познания экспериментального факта или теоретического положения почти все испытывают потребность в образе, в зримой картинке, в упрощенной модели. Быть может, это преувеличение, но кажется, что один из основных компонентов таланта ученого и педагога состоит в умении придумывать образы, аналогии и модели, способные разъяснить физическое явление и углубить его понимание.

Какой обязана быть модель? Что модель должна уметь? Что у нее можно просить и что от нее должно требовать? Просить можно о помощи и требовать должно отсутствия фальши, наличия хотя бы доли правды, относящейся к излагаемому явлению. В жизни к полуправде мы относимся презрительно, а по отношению к модели "полуправда" - высокая похвала. И конечно, модель должна быть наглядной, понятной без утомительных комментариев. Лучше всего, если вообще комментарии излишни, если наглядность настолько очевидна, что почти обретает доказательную силу.

Физике известно много выразительных и Красивых моделей, физике твердого тела - особенно. В этой статье будет рассказано об одной "живой" модели, великолепно иллюстрирующей (передающей, отражающей) структуру реального кристалла, имеющиеся в нем дефекты, их сложные взаимодействия. Модель эта не нова. Она была придумана выдающимся английским физиком Л. Бреггом еще в начале 40-х годов, а затем осуществлена им и его сотрудниками В. Ломером и Д. Наем. Так мы ее и будем называть: модель БЛН (Брегга-Ломера-Ная).

Что мы хотим моделировать?

Ответ четкий: реальный кристалл. Что значит "реальный кристалл"? Это значит - совокупность огромного числа одинаковых атомов или молекул, которые расположены в строгом порядке, образуя кристаллическую решетку. В некоторых местах строгий порядок может нарушаться, и эти нарушения означают наличие дефектов в кристалле. И еще одна очень важная характеристика: образующие кристалл атомы между собой взаимодействуют. О том, как взаимодействуют,- немного позже, а здесь лишь бесспорное утверждение: взаимодействуют! Потому что, если бы не взаимодействовали, был бы не кристалл, а груда беспорядочно нагроможденных атомов. Поддержание в кристалле порядка - прямое следствие взаимодействия между образующими его атомами.

Очень распространена так называемая мертвая модель кристалла. Она устроена так: деревянные или глиняные шарики, соединенные друг с другом ровными проволочками. Шарики - атомы, проволочки - символы связей между атомами, их "замороженного" взаимодействия. Замороженность взаимодействия и делает модель мертвой.

В этой модели атомы разного сорта - шарики различных размеров и цвета, разные расстояния между атомами - проволочки различной длины. Это разумная и очень полезная модель кристалла. Рассказывая о кристалле далеко не всю правду, она говорит о нем только правду, не фальшивит. В ней нет никаких видов движения атомов в кристалле, зато очень четко отражен порядок в их расположении. Мертвая модель кристалла - великолепный помощник, когда надо зримо представить себе пространственное расположение атомов или, например, те направления в кристалле, в которых он деформируется или проводит электрический ток легче, чем в других. Она незаменима, если нужно, пользуясь данными опытов и так называемыми общими соображениями, представить себе возможное расположение атомов в еще не изученном кристалле. Именно такое моделирование - шарики и проволочки - помогло сделать одно из самых крупных открытий XX века - установить структуру молекулы ДНК. Немалая заслуга мертвой модели!

Мы, однако, хотим моделировать не "мертвый", а "живой" кристалл. Для этого, очевидно, надо научиться моделировать взаимодействие между атомами в кристалле, оживлять замороженное в проволочках взаимодействие.

Взаимодействие между атомами в кристалле

Одна, пожалуй, самая важная характеристика этого взаимодействия непосредственно следует из простейшего факта: расстояние между двумя соседними атомами в реальном кристалле при постоянной температуре имеет вполне определенное значение. (Речь идет, разумеется, о расстоянии между положениями, около которых атомы совершают тепловые колебания. Амплитуда этих колебаний значительно меньше расстояния между атомами.)

Определенное расстояние - это означает, что если мы попытаемся его увеличить, атомы, противясь этому, будут притягиваться друг к другу, а если мы попытаемся его уменьшить - отталкиваться. Итак, только из факта наличия определенного расстояния между атомами следует, что взаимодействие между ними носит черты и притяжения, и отталкивания одновременно.

При некотором расстоянии между атомами (его мы и назвали определенным) силы притяжения и отталкивания оказываются равными по абсолютной величине. На этом расстоянии и расположены атомы в решетке.

Хорошо бы придумать такой прием моделирования, который передавал бы конкуренцию сил притяжения и отталкивания. Иначе говоря, "оживлял" бы взаимодействие между атомами в кристалле. Именно это и сделали авторы модели БЛН! В качестве строительных элементов в этой модели использованы не глиняные и не деревянные шарики, а ... маленькие мыльные пузырьки.

Взаимодействие мыльных пузырьков на воде

Они не безучастны друг к другу: два разобщенных мыльных пузырька на поверхности воды друг к другу притягиваются, а соприкоснувшись, отталкиваются друг от друга. Это можно наблюдать в очень простом опыте. Вот этот опыт.

Вначале раздобудем необходимое "оборудование": тарелку, медицинскую иглу от шприца, волейбольную камеру и зажим с регулируемым поджатием, с помощью которого можно было бы с различной силой сжимать резиновую трубку - отросток волейбольной камеры. Теперь подготовим опыт. Тарелку почти доверху заполним мыльной водой и добавим в нее несколько капель глицерина. Это для того, чтобы пузырьки, которые мы будем выдувать на поверхности мыльной воды, получались устойчивыми. Надуем волейбольную камеру, зажмем ее отросток и вставим в него иглу от шприца (разумеется, тупым концом). Опустим свободный конец иглы под воду (неглубоко)и немного ослабим зажим (рис. 70) - из иглы одна за другой начнут выходить строго одинаковые порции воздуха, которые будут превращаться в одинаковые мыльные пузырьки. Много пузырьков нам понадобится позже, а для первого опыта надо ухитриться создать всего два пузырька на некотором расстоянии друг от друга. Если сразу не получится - получится после пятой попытки! Удобно этот опыт проводить с пузырьками, диаметр которых 1-2 мм.

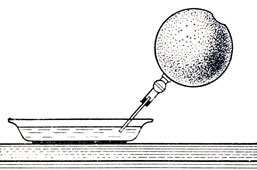
Рис. 70

Пузырьки созданы, теперь можно за ними наблюдать. Сначала очень медленно, а затем ускоряясь (без нашего вмешательства), пузырьки будут двигаться навстречу друг другу. Столкнувшись, они соприкоснутся не в точке, а как бы вдавятся один в другой. При этом несколько по-разному будут себя вести два одинаковых и два различных по размеру пузырька. Понаблюдайте!

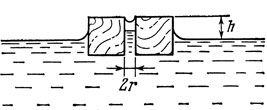
Рис. 71

Попытаемся понять происхождение силы, которая заставляет пузырьки самопроизвольно сближаться. Несколько удобнее сделать это, рассматривая не два мыльных пузырька, а две спички, параллельно лежащие на поверхности воды. И пузырьки, и спички смачиваются водой, на которой они плавают, поэтому общий характер взаимодействия для тех и других один и тот же. Удобство такой замены в том, что два плавающих пузырька, находясь близко один от другого, образуют вместе с жидкостью очень сложную поверхность, а спички - гораздо более простую (рис. 71). Сила, сближающая две плавающие спички, возникает вот как. Вода смачивает спички, поэтому ее поверхность возле спички искривляется. Кривизна поверхности приводит к появлению сил, действующих на жидкость. Это - силы, обусловленные поверхностным натяжением, направленные в нашем случае вертикально вверх (будем считать, что смачивание полное). Под действием этих сил жидкость поднимается по стенкам спичек, причем поднятие гораздо заметнее в области между спичками (см. рис. 71). Здесь жидкость оказывается как бы растянутой, давление в ней понижается по сравнению с атмосферным давлением на величину добавочного давления где σ - коэффициент поверхностного натяжения, d - расстояние между спичками, r = ^d/₂ - радиус кривизны поверхности жидкости. Следовательно, и сила давления жидкости на спички в области между спичками меньше по абсолютной величине силы атмосферного давления, действующей на спички снаружи. Таким образом, абсолютная величина силы, сближающей спички, равна

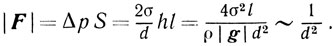
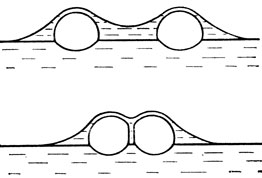
Рис. 72

Предскажем любопытное явление: так как сила F~l/d2, то спички, находящиеся в вязкой среде, будут сближаться со скоростью, увеличивающейся с уменьшением расстояния между ними. И не только спички. Пузырьки тоже сближаются, ускоряясь (рис. 72). В нашей лаборатории сближение пузырьков мы наблюдали так. Над кюветой с мыльным раствором и пузырьками расположили кинокамеру и, когда пузырьки начали сближаться, включили ее (рис. 73).

Рис. 73

Сближение пузырьков можно проследить вплоть до их столкновения. После того как пузырьки столкнулись, между ними начинает действовать сила отталкивания. Она обусловлена тем, что во взаимно вдавливающихся пузырьках (рис. 74) увеличивается давление газа, которое как бы расталкивает пузырьки.

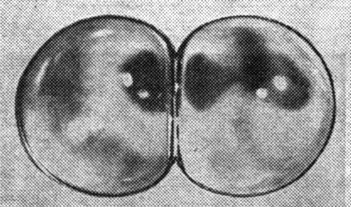
Рис. 74

Видимо, мыльные пузырьки вполне подходят для создания модели кристалла, если на поверхности мыльного раствора поселить не один, не два, а множество одинаковых пузырьков. Если радиус пузырька R = 5*10^-2 см, то на поверхности мыльного раствора в обыкновенной тарелке, радиус которой R_T ≈ 10 см, можно поселить N~(^R_T/_R)²~4*10⁴ пузырьков! Такой плот, составленный из пузырьков, между которыми действуют силы притяжения и отталкивания, представляет собой двумерную модель кристалла. Например, авторы этой очень красивой модели показали, что взаимодействие пузырьков, радиус которых R ∼ 10^-1 см, очень похоже на взаимодействие атомов в кристалле меди.

Модель в действии

Хорошо бы всем читателям показать кинофильм, в котором заснята модель БЛН в действии. Они увидели бы и идеальный кристалл, и кристалл с движущимися и взаимодействующими дефектами, и множество простых и сложных процессов, которые происходят в реальном кристалле. В статье можно лишь кое о чем рассказать и кое-что проиллюстрировать фотографиями и кинограммами.

С помощью модели БЛН оказалось возможным проверить некоторые следствия теории, построенной применительно к кристаллу, абсолютно свободному от каких-либо дефектов, так называемому идеальному кристаллу. Получить такой кристалл в натуре экспериментатор практически не может, а вот построить его из пузырьков оказалось просто и доступно (рис. 75).

Рис. 75

Один из самых распространенных дефектов в кристаллах - это пустая позиция в узле решетки, незамещенная атомом. Физики называют ее вакансией. В модели БЛН вакансия - это один лопнувший пузырек (рис. 76). В полном согласии со здравым смыслом и результатами опытов с реальными кристаллами модель БЛН свидетельствует о том, что объем одной вакансии немного меньше объема, приходящегося на занятую позицию. Действительно, после того как пузырек лопнул, его бывшие соседи немного переместятся в образовавшуюся пустоту и уменьшат ее. Невооруженным глазом это увидеть почти невозможно, но если спроектировать кино- или фотопленку на экран и тщательно промерить расстояния между пузырьками, можно убедиться, что по сравнению с занятой позицией вакансия немного сжата. Для физиков это свидетельство модели БЛН не просто качественная иллюстрация, оно имеет и количественную ценность.

Рис. 76

Очень часто в кристалле вследствие его предыстории оказывается постороннее включение, деформирующее кристалл. При решении многих задач физики кристаллов очень важно знать, как при этом смещаются атомы, окружающие включение. Оказывается, присутствие инородного включения чувствуют не только непосредственные соседи, но и атомы, расположенные от включения на значительном расстоянии. Модель БЛН это отчетливо иллюстрирует (см. рис. 76).

Большинство кристаллических тел являются поликристаллами. Это значит, что они состоят из множества произвольно ориентированных кристалликов, разделенных границами. Почти очевидно, что многие свойства поликристаллов (такие как механическая прочность или сопротивление электрическому току) должны зависеть от структуры границ. Модель БЛН и в этом вопросе оказалась очень полезной: подсказала кристаллофизикам, как изменяется структура границы в зависимости от взаимной ориентации граничащих кристалликов, от наличия примесей, расположенных на границе, и многое другое. Вот несколько примеров.

В поликристаллах может происходить процесс укрупнения одних участков (зерен) за счет других, в результате чего средний размер зерна увеличивается. Называется этот процесс рекристаллизацией и происходит он по причине очевидной: чем больше размер зерен, тем меньше суммарная поверхность границ, а значит, меньше и избыточная энергия, которая с границами связана. Энергия поликристалла при рекристаллизации уменьшается, следовательно, этот процесс может происходить самопроизвольно (поскольку приближает состояние устойчивого равновесия, в котором запас энергии минимален). На рис. 77 приведена кинограмма, иллюстрирующая последовательные этапы "поедания" крупным зерном расположенного в нем мелкого зерна.

Рис. 77

Оказывается (это предсказали теоретики и тщательно изучили экспериментаторы в опытах с реальными кристаллами), движущаяся граница между зернами "заглатывает" те вакансии, которые ей встречаются по пути. При этом граница не изменяет своего строения. Модель БЛН это явление отлично иллюстрирует (рис. 78).

Рис. 78

Ограниченность и "полуправда" модели БЛН

Допуская, что читатель проникся и уважением, и доверием к модели БЛН, придется его немного охладить, обратив внимание и на ограниченность модели, и на заключенную в ней "полуправду".

Модель БЛН способна моделировать лишь одну структуру: двумерную, гексагональную и плотноупакованную. А истинные кристаллы имеют множество структур. Возможности "мертвой" модели непомерно богаче, в ней можно располагать несметным числом способов и, следовательно, можно моделировать любую мыслимую структуру. Кроме того, модель БЛН в своем современном варианте - двумерна. Ее авторы пытались осуществить и пространственную (многослойную) пузырьковую модель, но экспериментировать с ней оказалось совсем не просто, и модель не привилась. В нашей лаборатории мы осуществили и двумерную, и трехмерную модели БЛН и убедились, что трехмерная фактически нежизнеспособна.

Не будем упрекать модель в ее слабостях, о которых упомянули и о которых умолчали. Будем ей благодарны за ее сильные стороны.