Как с помощью проволоки измерить длину световой волны (Н. Ростовцев)

На пути света, идущего от точечного источника, непосредственно перед глазом Г (на расстоянии 2-3 мм от него) поместим тонкую проволоку П диаметром 0,05-0,12 мм, расположенную вертикально (рис. 120). Тогда слева и справа от источника света мы увидим узкую светлую полоску. Она возникает вследствие дифракции света, поэтому будем называть ее дифракционной полоской. Роль точечного источника света при этих наблюдениях может играть малое отверстие О в ширме А, установленной перед лампочкой, или лампочка от карманного фонаря, отстоящая от места наблюдения на расстоянии 1-1,5 м. Проволоку П можно заменить тонкой нитью или волосом.

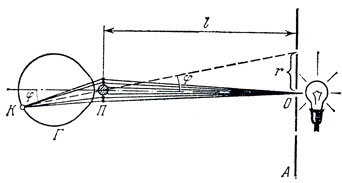
Рис. 120

При внимательном рассмотрении дифракционной полоски в ее середине виден белый участок с красноватыми краями - нулевой максимум; с обеих сторон он ограничен узкими темными промежутками - первыми минимумами. Затем идут цветные участки, в которых при удалении от центра полоски зеленовато-голубая окраска постепенно переходит в красную. За красным краем этих участков опять следуют темные промежутки - вторые минимумы. Далее картина повторяется с той лишь разницей, что минимумы просматриваются все хуже, и в конце концов светлые участки сливаются в сплошную полоску. Наблюдения, проведенные с проволокой разного диаметра, показывают, что расстояние между двумя соседними минимумами тем больше, чем меньше диаметр проволоки.

Представляет интерес и другое наблюдение. Проволоку, с помощью которой мы только что наблюдали дифракцию, осторожно зажмем между губками штангенциркуля и сейчас же вытянем ее из губок. Тогда ширина щели между губками будет равна толщине проволоки. Через эту щель с того же расстояния, как и при наблюдении дифракции от проволоки, посмотрим на освещенное отверстие О. По обе стороны от него мы увидим дифракционную полоску с точно такими же расстояниями между минимумами и максимумами, как и при дифракции от проволоки. Это наблюдение является прекрасной иллюстрацией к теореме Бабине, согласно которой дифракционные картины от экрана и равного ему по ширине отверстия совершенно одинаковы вне области прямого пучка.

Теперь кусок проволоки, с которой проводились наблюдения дифракционной полоски, скомкаем в моток, имеющий форму диска диаметром с копеечную монету. Для этого достаточно взять проволоку длиной 2-3 м. Поместим получившийся моток перед глазом и посмотрим на точечный источник света. Тогда мы увидим венцы - центральный белый круг с красноватыми краями, окруженный цветными кольцами. Венцы отделяются друг от друга узкими темными кольцами - минимумами. Каждое темное кольцо следует за красным краем предыдущего венца. Причем, если расстояние до источника то же, что и при наблюдении дифракции от проволоки, диаметры темных колец оказываются равными расстояниям между соответствующими минимумами дифракционной полоски. Венцы видны тем лучше, чем меньше диаметр проволоки.

Почему же возникают венцы при помещении мотка проволоки на пути лучей, идущих от точечного источника света? Каждый малый участок проволоки, находящийся перед глазом, дает свою дифракционную полоску, расположенную симметрично относительно источника света. Вследствие различной ориентации участков проволоки в мотке различные направления имеют и возникающие от них дифракционные полоски, причем все они пересекаются в одной точке, совпадающей с источником света. Толщина всех участков проволоки одинакова, поэтому минимумы одного и того же порядка располагаются во всех дифракционных полосках на одинаковом расстоянии от источника света и сливаются в темные кольца. Цветные участки, заключенные между минимумами, сливаются при этом в цветные кольца.

Найдем теперь условия возникновения минимумов при дифракции от проволоки толщиной d и щели такой же ширины. Учитывая тот факт, что расстояния между минимумами в том и другом случаях одинаковы, достаточно провести расчет или для проволоки или для щели. С целью упрощения проведем расчет для щели.

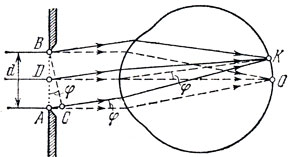
Рис. 121

Рассмотрим волны, которые не меняют своего направления после прохождения через щель (на рис. 121 они изображены штриховыми линиями). Глаз сводит их на сетчатку в точку О. Волны от всех точек щели в этом месте усиливают друг друга, так как они попадают в глаз без разности хода и в точке О имеют одинаковые фазы. Поэтому в окрестности точки О образуется нулевой максимум. Волны, которые дифрагируют под углом φ к первоначальному направлению, глаз сводит в точку К, где при наложении они интерферируют. Результат интерференции зависит от разности хода между лучами, исходящими из крайних точек щели А и В. Проведем отрезок ВС перпендикулярно лучу, выходящему из точки А. Образовавшийся отрезок АС равен разности хода между крайними лучами. Из рисунка следует, что AC = d sin φ, где d - ширина щели.

Расчеты показывают, что при дифракции от прямоугольной щели минимумы наблюдаются, когда разность хода волн от крайних точек щели

где λ - длина световой волны, k - номер (порядок) минимума (k = 1, 2, 3, ...).

Покажем справедливость формулы (1) для первого минимума, т. е. для k = 1. Пусть вторичные волны от всех точек щели распространяются под таким углом φ, что выполняется условие

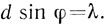
(2)

Мысленно разобьем щель на две параллельные прямоугольные полоски (зоны) AD и DB одинаковой ширины d/2. В силу условия (2) разность хода между лучами, выходящими из точек А и D, равна λ/2. Такая же разность хода λ/2 в этом случае будет и между лучами, выходящими из любых двух точек щели, которые отстоят друг от друга на расстоянии d/2. Волны с разностью хода λ/2 при наложении гасят друг друга, поэтому при выполнении условия (2) все волны от зоны AD погасят волны от зоны DB и в точке К будет наблюдаться первый минимум.

Таким же способом можно показать, что следующий (второй) минимум будет наблюдаться при выполнении условия d sin φ = 2λ. В этом случае щель следует разбить на четыре равных зоны. Разность хода между волнами от первой и второй, и от третьей и четвертой зон будет равна λ/2. Поэтому волна от первой зоны погасит волну от второй зоны, а волна от третьей - волну от четвертой зоны, и в месте наложения этих волн на сетчатке будет наблюдаться второй минимум.

Из формулы (1) следует, что длину световой волны можно определить по формуле

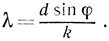
(3)

Измерения λ значительно упрощаются, если использовать простейшее измерительное устройство, называемое эриометром. Для изготовления эриометра берут квадратный кусок картона со стороной 10-15 см и в его середине проводят окружность радиусом r = 20-30 мм. В центре окружности прокалывают отверстие диаметром 2-3 мм, а вдоль окружности прокалывают 6-8 отверстий меньшего диаметра.

При измерениях эриометр А устанавливают непосредственно перед лампочкой накаливания. Отойдя от эриометра на расстояние 1-2 м, находят такое положение, при котором через отверстие О в глаз наблюдателя попадают лучи, идущие непосредственно от одного из участков раскаленной нити. Затем перед глазом помещают моток проволоки и добиваются хорошего видения венцов, перемещая моток в направлении, перпендикулярном лучам. Изменяя расстояние между эриометром и глазом, находят положение, при котором окружность эриометра с отверстиями совпадает с серединой темного кольца с номером k (на рис. 120 изображен случай, когда k = 2).

Как видно из рис. 120, тангенс угла дифракции φ для темного кольца подсчитывается по формуле tg φ = r/l, где r - радиус окружности эриометра, l - расстояние от эриометра до мотка проволоки. При малых углах дифракции, с которыми приходиться иметь дело при таких измерениях, справедливо соотношение

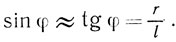
Подставляя значение sin φ в выражение (1), получаем формулу для определения длины волны:

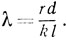
(4)

Радиус окружности эриометра r нам заранее известен. Расстояние l легко измерить. Номер темного кольца k определяется при наблюдении венцов. Диаметр проволоки d, если он не известен, измеряют микрометром.

Если измерения производят в белом свете, то по формуле (4) находят эффективную длину световой волны, к которой наиболее чувствителен наш глаз. Она приблизительно равна 0,56 мкм. Световые волны такой длины соответствуют зеленой части спектра.

Венцы могут возникать при дифракции света и на круглых преградах. Наблюдать их можно следующим образом. Насыпем на стеклянную пластинку небольшое количество ликоподия (ликоподий - порошок из спор плауна, его можно купить в аптеке). Легким постукиванием торца пластины о стол удалим излишек порошка. Если через такую пластинку посмотреть на точечный источник света, то мы увидим венцы. Роль круглых преград в этом опыте играют споры приблизительно сферической формы. Особенно яркие венцы возникают при рассматривании капли крови, сжатой между двумя стеклянными пластинами. В этом случае венцы возникают при дифракции на эритроцитах - красных кровяных тельцах.

Венцы, возникающие от круглых и прямоугольных преград, несколько отличаются друг от друга. Условие минимумов для венцов от прямоугольных преград выражается соотношением (1). Для венцов от круглых препятствий оно имеет вид:

Здесь d - диаметр круглого экрана. Применяя эриометр, по формуле (5) можно определить средний диаметр спор плауна и эритроцитов без микроскопа!

В природе венцы наблюдаются вокруг Солнца, Луны и даже планет. Они возникают при прохождении света от светила через скопления взвешенных в воздухе водяных капелек или ледяных кристалликов (через неплотное облако, например). Хорошо видимые венцы получаются лишь в том случае, когда в облаке преобладают капельки одинакового диаметра или кристаллики одинаковой толщины. Если капельки или кристаллики льда имеют неодинаковые размеры, то кольца разных цветов налагаются друг на друга и вокруг светила мы видим беловатый круг. Этим обусловливается то обстоятельство, что венцы около Луны особенно часто появляются вечерами ясных дней. В такие вечера происходит слабая конденсация находящегося в воздухе водяного пара в виде маленьких капелек или кристалликов одинакового размера. Иногда венцы наблюдаются при прохождении света от удаленного фонаря через слой тумана или оконное стекло, покрытое тонким слоем ледяных кристалликов или капелек сконденсировавшейся влаги.

1. По известной эффективной длине волны (~ 0,56 мкм) найдите с помощью эриометра диаметр нитей, из которых изготавливают капроновые чулки и ленты.
2. Как по виду венцов определить, состоит ли облако из водяных капелек или кристалликов льда?
3. Угловой диаметр Луны равен 32'. Оцените диаметр капелек в облаке, если угловой радиус центрального круга в венцах в четыре раза больше углового диаметра Луны.